Números cuánticos: para qué sirven y cuáles son
Los números cuánticos se usan para describir el estado cuántico de los electrones en el átomo y se originan en la solución de la ecuación de Schrödinger para el más sencillo de todos: el de hidrógeno.
La ecuación de Schrödinger es una ecuación diferencial, cuyas soluciones son funciones de onda y se denotan mediante la letra griega ψ. Se pueden plantear infinitas soluciones, y su cuadrado equivale a la probabilidad de encontrar al electrón en una pequeña región del espacio, llamada orbital.
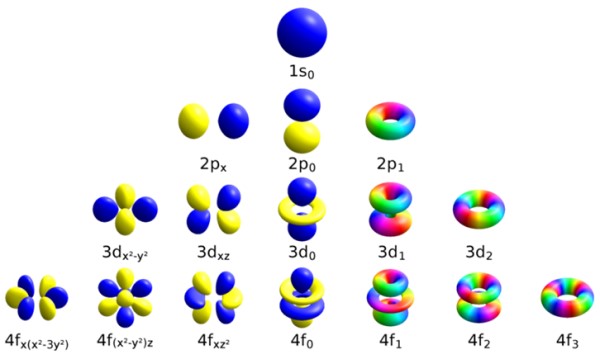
Cada orbital tiene características definidas que lo distinguen de los otros, como por ejemplo la energía, el momento angular y el espín, una propiedad enteramente cuántica del electrón y que es responsable, entre otras cosas, de los efectos magnéticos.
La manera de identificar a cada orbital es distinguirlo mediante un conjunto de números que lo describen, y estos son precisamente los números cuánticos:
-n: es el número cuántico principal.
-ℓ: el número cuántico azimutal.
-mℓ, es el número magnético.
-ms, el número de espín.
Índice del artículo
Los números cuánticos sirven para describir el estado de los electrones en el interior del átomo. Aquel modelo atómico en el que el electrón da vueltas alrededor del núcleo es inexacto, porque no es consistente con la estabilidad atómica ni tampoco con una gran cantidad de fenómenos físicos observados.
Por eso el danés Niels Bohr (1885-1962) realizó en 1913 una propuesta audaz: el electrón solamente puede encontrarse en ciertas órbitas estables, cuyo tamaño depende de un número entero llamado n.
Más adelante, en 1925, el también físico austríaco Erwin Schrödinger (1887-1961) planteó una ecuación diferencial en derivadas parciales, cuyas soluciones describen al átomo de hidrógeno. Son la funciones de onda ψ mencionadas al comienzo.
Dicha ecuación diferencial incluye las tres coordenadas espaciales más el tiempo, pero cuando este no se incluye, la solución de la ecuación de Schrödinger es análoga a la de una onda estacionaria (una onda que se propaga entre ciertos límites).
La ecuación de Schrödinger independiente del tiempo se resuelve en coordenadas esféricas y la solución se escribe como el producto de tres funciones, una para cada variable espacial. En este sistema de coordenadas, en vez de utilizar las coordenadas de los ejes cartesianos x, y y z se emplean las coordenadas r, θ y φ. De esta manera:
ψ (r, θ, φ) = R(r)⋅f (θ)⋅g (φ)
La función de onda es intangible, no obstante la mecánica cuántica nos dice que la amplitud al cuadrado:
|ψ (r, θ, φ)|2
Es decir, que el módulo o valor absoluto de la función de onda, elevado al cuadrado, es un número real que representa la probabilidad de dar con el electrón, en una cierta región alrededor del punto cuyas coordenadas son r, θ y φ.
Y este hecho sí es algo más concreto y tangible.
Para encontrar la función de onda, hay que resolver tres ecuaciones diferenciales ordinarias, una para cada variable r, θ y φ.
Las soluciones de cada ecuación, que serán las funciones R(r), f (θ) y g (φ), contienen los primeros tres números cuánticos mencionados.
A continuación describimos brevemente la naturaleza de cada número cuántico. Los tres primeros, como se dijo previamente, surgen de las soluciones de la ecuación de Schrödinger.
El cuarto número lo añadió Paul Dirac (1902 – 1984) en 1928.
Se denota mediante n e indica el tamaño del orbital permitido, así como la energía del electrón. Cuanto mayor sea su valor, más alejado está el electrón del núcleo y su energía será mayor también, pero a cambio reduce su estabilidad.
Este número surge de la función R(r), que es la probabilidad de encontrar al electrón a cierta distancia r del núcleo, la cual se determina mediante:
-Constante de Planck: h = 6,626 × 10 -34 J.s
-Masa del electrón me = 9.1 × 10-31 kg
-Carga del electrón: e = 1.6 × 10-19 C.
-Constante electrostática: k = 9 × 10 9 N.m2/C2
Cuando n = 1 corresponde al radio de Bohr que vale aproximadamente 5.3 × 10−11 m.
Salvo la primera capa, las demás se subdividen en subcapas o subniveles. Cada capa tiene una energía en electrón voltio dada por:
- K (n=1)
- L (n =2)
- M (n=3)
- N (n=4)
- O (n =5)
- P (n=6)
- Q (n=7).
En teoría no hay límite superior para n, pero en la práctica se observa que solamente llega hasta n = 8. La menor energía posible corresponde a n = 1 y es la del estado fundamental.
Denotado mediante la letra ℓ cursiva, este número determina la forma de los orbitales, al cuantificar la magnitud del momento angular orbital del electrón.
Puede tomar valores enteros y positivos comprendidos entre 0 y n–1, por ejemplo:
-Cuando n = 1, entonces ℓ= 0 y hay un único subnivel.
-Si n = 2, entonces ℓ puede valer 0 o 1, por lo que se tienen dos subniveles.
-Y si n = 3, entonces ℓ asume los valores 0, 1 y 2 y hay 3 subniveles.
Se puede seguir de esta manera indefinidamente, aunque como se dijo antes, en la práctica n llega hasta 8. Los subniveles se denotan mediante las letras: s, p, d, f y g y van aumentando en energía.
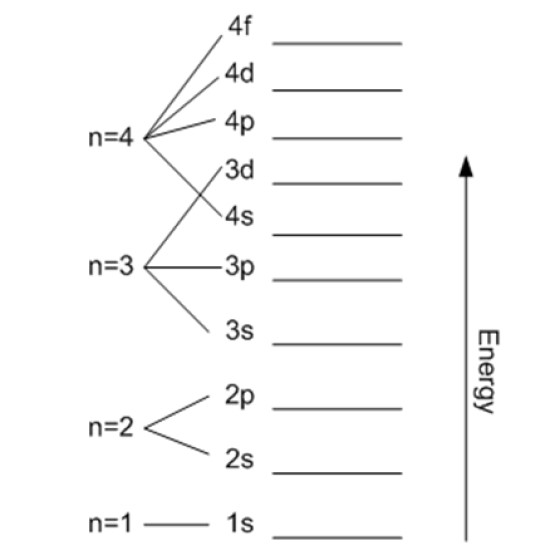
Este número decide la orientación del orbital en el espacio y su valor depende del de ℓ.
Para un ℓ dado, hay (2ℓ+1) valores enteros de m ℓ, que corresponden a los respectivos orbitales. Estos son:
-ℓ , (- ℓ+1), …0,… (+ℓ -1), +ℓ.
Ejemplo
Si n = 2, sabemos que ℓ = 0 y ℓ= 1, entonces m ℓ toma los siguientes valores:
-Para ℓ=0: m ℓ = 0.
-Para ℓ = 1: m ℓ = -1, m ℓ = 0, m ℓ = +1
El orbital n = 2 tiene dos subniveles, el primero con n=2, ℓ = 0 y m ℓ = 0. Luego tenemos el segundo subnivel: n = 2, ℓ = 1, con 3 orbitales:
- n = 2, ℓ = 1, m ℓ = -1
- n = 2, ℓ = 1, m ℓ = 0
- n = 2, ℓ = 1, m ℓ = +1
Los tres orbitales tienen la misma energía pero diferente orientación espacial.
Al resolver la ecuación de Schrödinger en tres dimensiones, surgen los números ya descritos. Sin embargo, en el hidrógeno se observa una estructura aún más fina que dichos números no bastan para explicar.
Por ello, en 1921 otro físico, Wolfgang Pauli, propuso la existencia de un cuarto número: el número de espín ms, que toma valores de +½ o -½.
Con este número se describe una propiedad muy importante del electrón, que es el espín, palabra que proviene del inglés spin (girar sobre sí mismo). Y el espín a su vez está relacionado con las propiedades magnéticas del átomo.
Una manera de entender el espín es imaginando que el electrón se comporta como un diminuto dipolo magnético (un imán con polos norte y sur), gracias a una rotación alrededor sobre su propio eje. El giro puede ser en el mismo sentido que las agujas del reloj, o bien en sentido contrario.
Si bien Pauli sugirió la existencia de este número, los resultados de un experimento llevado a cabo por Otto Stern y Walter Gerlach en 1922 ya lo habían anticipado.
Estos científicos consiguieron dividir en dos un haz de átomos de plata mediante la aplicación de un campo magnético no uniforme.
El valor de ms no depende de n, ℓ y m ℓ. En forma gráfica, se representa mediante una flecha: una flecha hacia arriba indica giro horario y una hacia abajo el giro antihorario.
Principio de exclusión de Pauli
El comportamiento de los electrones en el átomo se resume en el principio de exclusión de Pauli, el cual afirma que dos electrones de un átomo no pueden existir en el mismo estado cuántico.
Por lo tanto, cada electrón debe tener un conjunto diferente de números cuánticos n, ℓ, m ℓ y ms.
La importancia de los números cuánticos y este principio radica en el entendimiento de las propiedades de los elementos en la tabla periódica: los electrones se organizan en capas según n, y luego en sub-capas de acuerdo a ℓ y el resto de los números.
- Alonso, M. 1971. Fundamentos cuánticos y estadísticos. Fondo Educativo Interamericano.
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
- Chang, R. 2013. Química. 11va. Edición. Mc Graw Hill Educación.
- Eisberg-Resnick. 1989. Física Cuántica. Limusa – Wiley.
- Giambattista, A. 2010. Physics. 2nd. Ed. McGraw Hill.
- Rex, A. 2011. Fundamentos de Física. Pearson.
- Tippens, P. 2011. Física: Conceptos y Aplicaciones. 7ma Edición. McGraw Hill.
