10 características del cuadrado
La característica del cuadrado principal es el hecho de que está formados por cuatro lados, los cuales tienen exactamente las mismas medidas. Estos lados se organizan de modo que formen cuatro ángulos de rectos (de 90°).
El cuadrado es una figura geométrica básica, objeto de estudio de la geometría plana, puesto que se trata de una figura bidimensional (que tiene ancho y alto pero carece de profundidad).
Los cuadrados son polígonos. De manera más concreta, son polígonos (a) cuadriláteros por tener cuatro lados, (b) equiláteros por tener lados que miden lo mismo y (c) equiángulos por tener ángulos con la misma amplitud.
Estas dos últimas propiedades del cuadrado (equilátero y equiángulo) se pueden resumir en una sola palabra: regular. Esto quiere decir que los cuadrado son polígonos cuadriláteros regulares.
Al igual que las demás figuras geométricas, el cuadrado tiene un área. Esta se puede calcular multiplicando uno de sus lados por sí mismo. Por ejemplo, si tenemos un cuadrado que mide 4 mm, su área sera de 16 mm2.
Características destacadas de los cuadrados
1- Número de lados y dimensión
Los cuadrado están compuestos por cuatro lados que miden lo mismo. Además, los cuadrados son figuras bidimensionales, lo que quiere decir que sólo tienen dos dimensiones: ancho y alto.
La característica básica de los cuadrados es que tienen cuatro lados. Son figuras planas, por lo que se denominan bidimensionales.
2- Polígono
Los cuadrados son un polígono. Esto quiere decir que los cuadrados son figuras geométricas delimitadas por una línea cerrada formada por segmentos consecutivos de recta (línea poligonal cerrada).
Específicamente se trata de un polígono cuadrilátero porque tiene cuatro lados.
3- Polígono equilátero
Se dice que un polígono es equilátero cuando todos lados tienen la misma medida. Esto quiere decir que si uno de los lados del cuadrado mide 2 metro, todos los lados medirán dos metros.
Los cuadrados son equiláteros, lo que quiere decir que todos su lados miden lo mismo.
En la imagen, se muestra un cuadrado con lados iguales de 5 cm.
4- Polígono equiángulo
Se dice que un polígono es equiángulo cuando todos los ángulos que forma la línea poligonal cerrada tienen la misma medida.
Todos los cuadrados están conformados por cuatro ángulos rectos (es decir, ángulos de 90 °), sin importar las medidas del ángulo en particular: tanto un cuadrado de 2 cm x 2 cm como un cuadrado de 10 m x 10 m tienen cuatro ángulos rectos.
Todos los cuadrados son equiángulos porque sus ángulos tienen la misma amplitud. Es decir, 90 °.
5- Polígono regular
Cuando un polígono es equilátero y a la vez equiángulo, se considera que este es un polígono regular.
Debido a que el cuadrado tiene lados que miden lo mismo y ángulos de igual amplitud, se puede decir que este es un polígono regular.
Los cuadrados tienen tanto lados de igual medida como ángulos de igual amplitud, por lo que se trata de polígonos regulares.
En la imagen anterior, se muestra un cuadrado con cuatro lados de 5 cm y cuatro ángulos de 90 °.
6- El área de un cuadrado
El área de un cuadrado es igual al producto de un lado por otro lado. Debido a que los dos lados tienen exactamente la misma medida, se puede simplificar la fórmula diciendo que el área de este polígono es igual a uno de sus lados al cuadrado, es decir (lado)2.
Algunos ejemplos del cálculo del área de un cuadrado son:
– Cuadrado con lados de 2 m: 2 m x 2 m = 4 m2
– Cuadrados con lados de 52 cm: 52 cm x 52 cm = 2704 cm2
– Cuadrado con lados de 10 mm: 10 mm x 10 mm = 100 mm2
El cuadrado presentado en la imagen tiene lados de 5 cm.
Su área será el producto de 5 cm x 5 cm, o lo que es lo mismo (5cm)2
En este caso, el área del cuadrado es 25 cm2
7- Los cuadrados son paralelogramos
Los paralelogramos son un tipo de cuadrilátero que tienen dos pares de lados paralelos. Esto quiere decir que un par de lados se enfrenta entre sí, mientras que lo mismo sucede con el otro par.
Existen cuatro tipos de paralelogramos: los rectángulos, los rombos, los romboides y los cuadrados.
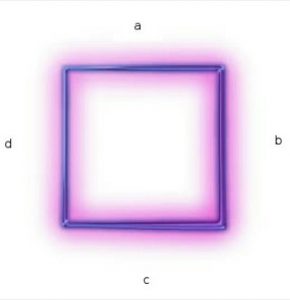
Los cuadrados son paralelogramos porque tienen dos pares de lados que son paralelos.
Los lados (a) y (c) son paralelos.
Los lados (b) y (d) son paralelos.
8- Los ángulos opuestos son congruentes y los consecutivos son complementarios
Que dos ángulos sean congruentes quiere decir que estos tienen la misma amplitud. En este sentido, como un cuadrado tienen todos los ángulos de la misma amplitud, se puede decir que los ángulos opuestos son congruentes.
Por su parte, el hecho de que dos ángulos consecutivos sean complementarios quiere decir que la suma de estos dos es igual a un ángulo llano (aquel que tiene una amplitud de 180°).
Los ángulos de un cuadrado son ángulos rectos (de 90 °), por lo que su suma da 180 °.
9- Se construyen a partir de una circunferencia
Para construir un cuadrado, se dibuja una circunferencia. Posteriormente, se procede a trazar dos diámetros sobre esta circunferencia; dichos diámetros se deben ser perpendiculares, formando una cruz.
Una vez trazados los diámetros, tendremos cuatro puntos en los que los segmentos de recta cortan la circunferencia. Si se unen estos cuatro puntos, se tendrá como resultado un cuadrado.
10- Los diagonales se cortan en su punto medio
Los diagonales son líneas rectas que se trazan de un ángulo a otro que le es opuesto. En un cuadrado, se pueden trazar dos diagonales. Estas diagonales se cruzarán en el punto medio del cuadrado.
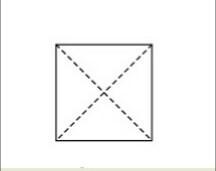
En la imagen, las líneas punteadas representan las diagonales. Como se puede apreciar, estas rectas se cruzan exactamente en el medio del cuadrado.
Referencias
- Square. Recuperado el 17 de julio de 2017, de en.wikipedia.org
- Square and its properties. Recuperado el 17 de julio de 2017, de mathonpenref.com
- Properties of Rhombuses, Rectangels and Squares. Recuperado el 17 de julio de 2017, de dummies.com
- The properties of a square. Recuperado el 17 de julio de 2017, de coolmth.com
- Square. Recuperado el 17 de julio de 2017, de onlinemschool.com
- Properties of Squares. Recuperado el 17 de julio de 2017, de brlliant.org.
