Grados de libertad: cómo calcularlos, tipos, ejemplos

Los grados de libertad en estadística son el número de componentes independientes de un vector aleatorio. Si el vector tiene n componentes y hay p ecuaciones lineales que relacionan sus componentes, entonces el grado de libertad es n-p.

El concepto de grados de libertad también aparece en mecánica teórica, donde a groso modo equivalen a la dimensión del espacio donde la partícula se mueve, menos el número de ligaduras.

En este artículo se tratará el concepto de grados de libertad aplicado a la estadística, pero un ejemplo mecánico es más fácil de visualizar en forma geométrica.

Índice del artículo

• 1 Tipos de grados de libertad
  • 1.1 En un caso mecánico
  • 1.2 En un conjunto de valores aleatorios
• 2 Ejemplos
  • 2.1 Varianza y grados de libertad
  • 2.2 En la distribución Chi cuadrado
  • 2.3 En el contraste de hipótesis (Con ejemplo resuelto)
• 3 Referencias

Tipos de grados de libertad

Según el contexto en el que se aplique, la forma de hacer el cálculo del número de grados de libertad puede variar, pero la idea subyacente siempre es la misma: dimensiones totales menos número de restricciones.

En un caso mecánico

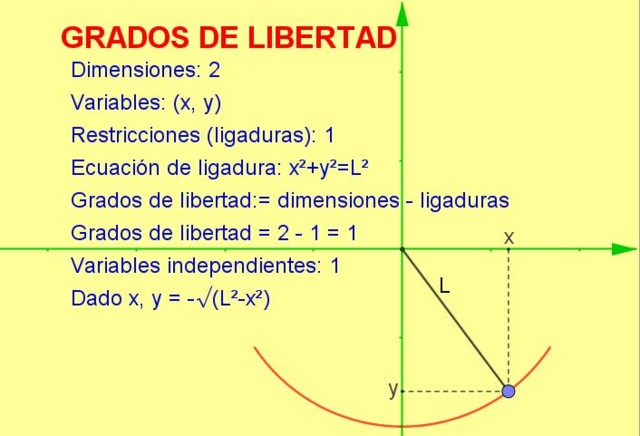
Consideremos una partícula que oscila atada a una cuerda (un péndulo) que se mueve en el plano vertical x-y (2 dimensiones). Sin embargo, la partícula está obligada a moverse sobre la circunferencia de radio igual a la longitud de la cuerda.

Como la partícula solo puede moverse sobre esa curva, el número de grados de libertad es 1. Esto se puede visualizar en la figura 1.

La forma de calcular el número de grados de libertad es tomando la diferencia del número de dimensiones menos el número de restricciones:

grados de libertad := 2 (dimensiones) – 1 (ligadura) = 1

Otra explicación que nos permite llegar al resultado es la siguiente:

-Sabemos que la posición en dos dimensiones está representada por un punto de coordenadas (x, y).

-Pero como el punto debe cumplir la ecuación de la circunferencia (x² + y² = L²) para un valor dado de la variable x, la variable y queda determinada por dicha ecuación o restricción.

De este modo, solo una de las variables es independiente y el sistema tiene un (1) grado de libertad.

En un conjunto de valores aleatorios

Para ilustrar lo que significa el concepto supongamos el vector

x = (x₁, x₂, …,x_n)

Que representa la muestra de n valores aleatorios normalmente distribuidos. En este caso el vector aleatorio x tiene n componentes independientes y por lo tanto se dice que x tienen grados de libertad.

Construyamos ahora el vector r de los residuos

r = (x₁ – , x₂ – , …., x_n – )

Donde representa la media de la muestra, que se calcula así:

= (x₁ + x₂ + ….+ x_n) / n

Entonces la suma

(x₁ – )+(x₂ – )+ ….+(x_n – )= (x₁ + x₂ + ….+ x_n) – n= 0

Es una ecuación que representa una restricción (o ligadura) en los elementos del vector r de los residuos, ya que si se conocen n-1 componentes del vector r, la ecuación de restricción determina la componente desconocida.

Por lo tanto el vector r de dimensión n con la restricción:

∑(x_i – ) = 0

Tiene (n – 1) grados de libertad.

De nuevo se aplica que el cálculo del número de grados de libertad es:

grados de libertad := n (dimensiones) – 1 (restricciones) = n-1

Ejemplos

Varianza y grados de libertad

La varianza s² se define como el promedio del cuadrado de las desviaciones (o residuos) de la muestra de n datos:

s² = (r•r) / (n-1)

donde r es el vector de los residuos r = (x1 – , x2 – , …., xn – ) y el punto grueso (•) es el operador producto escalar. Alternativamente, la fórmula de la varianza puede escribirse de la siguiente manera:

s² = ∑(x_i – )² / (n-1)

En todo caso, debe notarse que al calcular el promedio del cuadrado de los residuos se divide entre (n-1) y no entre n, ya que como se discutió en la sección previa, el número de grados de libertad del vector r es (n-1).

Si para el cálculo de la varianza se dividiese entre n en vez de (n-1), el resultado tendría un sesgo que es muy significativo para valores de n menores a 50.

En la literatura aparece también la fórmula de la varianza con el divisor n en vez de (n-1), cuando se trata de la varianza de una población.

Pero el conjunto de la variable aleatoria de los residuos, representada por el vector r, si bien tiene dimensión n, solo tiene (n-1) grados de libertad. No obstante, si el número de datos es suficientemente grande (n>500), ambas fórmulas convergen al mismo resultado.

Las calculadoras y las hojas de cálculo ofrecen las dos versiones de la varianza y de la desviación estándar (que es la raíz cuadrada de la varianza).

Nuestra recomendación, en vista del análisis presentado aquí, es elegir siempre la versión con (n-1) cada vez que se requiera calcular la varianza o la desviación estándar, para evitar resultados con sesgo.

En la distribución Chi cuadrado

Algunas distribuciones de probabilidad en variable aleatoria continua dependen de un parámetro denominado grado de libertad, es el caso de la distribución Chi cuadrado (χ²).

El nombre de dicho parámetro proviene justamente de los grados de libertad del vector aleatorio subyacente al que se aplica esta distribución.

Suponga que se tiene g poblaciones, de las que se toman muestras de tamaño n:

X₁ = (x1₁, x1₂, …..x1_n)

X2 = (x2₁, x2₂, …..x2_n)

….

X_j = (xj₁, xj₂, …..xj_n)

….

Xg = (xg₁, xg₂, …..xg_n)

Una población j que tiene media y desviación estándar Sj, sigue la distribución normal N(, Sj ).

La variable tipificada o normalizada zj_i se define como:

zj_i = (xj_i – ) / Sj.

Y el vector Zj se define así:

Zj = (zj₁, zj₂, …,zj_i, …, zj_n) y sigue la distribución normal tipificada N(0,1).

Entonces la variable:

Q =( (z1₁ ^2 + z2₁^2+…. + zg₁^2),…., (z1_n^2 + z2_n^2+…. + zg_n^2) )

sigue la distribución χ²(g) llamada la distribución chi cuadrado con grado de libertad g.

En el contraste de hipótesis (Con ejemplo resuelto)

Cuando se quiere hacer un contraste de hipótesis en base a cierto conjunto de datos aleatorios, se requiere conocer el número de grados de libertad g para poder aplicar el test Chi cuadrado.

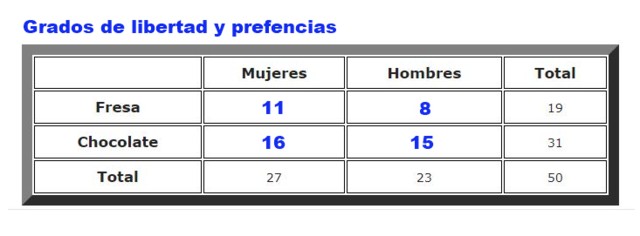
Como ejemplo se analizarán los datos recabados sobre las preferencias de helados de chocolate o fresa entre hombres y mujeres en cierta heladería. La frecuencia con la que hombres y mujeres eligen fresa o chocolate, se resume en la figura 2.

En primer lugar se calcula la tabla de frecuencias esperadas, la cual se elabora multiplicando el total de filas por el total de columnas, dividido entre total de datos. El resultado se muestra en la siguiente figura:

Luego se procede a calcular el Chi cuadrado (a partir de los datos) mediante la siguiente fórmula:

χ² = ∑ (F_o – F_e)² / F_e

Donde F_o son las frecuencias observadas (Figura 2) y F_e son las frecuencias esperadas (Figura 3). La sumatoria va sobre todas las filas y las columnas, que en nuestro ejemplo dan cuatro términos.

Después de hacer las operaciones se obtiene:

χ² = 0,2043.

Ahora es necesario comparar con el Chi cuadrado teórico, el cual depende del número de grados de libertad g.

En nuestro caso este número se determina de la siguiente manera:

g = (#filas – 1) (#columnas – 1) = (2 – 1) (2 – 1) = 1 * 1 = 1.

Resulta que el número de grados de libertad g de este ejemplo es 1.

Si se quiere comprobar o rechazar la hipótesis nula (H0: no hay correlación entre SABOR y GÉNERO) con un nivel de significancia del 1% se procede a calcular el valor Chi cuadrado teórico con grado de libertad g=1.

Se busca el valor que hace que la frecuencia acumulada sea (1 – 0.01) = 0.99, es decir 99%. Este valor (que puede obtenerse de las tablas) es 6.636.

Como el Chi teórico supera al calculado, entonces se verifica la hipótesis nula.

Es decir, que con los datos recabados, no se observa relación entre las variables SABOR y GÉNERO.

Referencias

1. Minitab. ¿Qué son los grados de libertad? Recuperado de: support.minitab.com.
2. Moore, David. (2009) Estadística aplicada básica. Antoni Bosch editor.
3. Leigh, Jennifer. Cómo calcular grados de libertad en modelos estadísticos. Recuperado de: geniolandia.com
4. Wikipedia. Grado de libertad (estadística). Recuperado de: es.wikipedia.com
5. Wikipedia. Grado de libertad (física). Recuperado de: es.wikipedia.com