Medidas de posición, de tendencia central y dispersión

Las medidas de tendencia central, de dispersión y de posición, son valores que se usan para interpretar adecuadamente un conjunto de datos estadísticos. Estos pueden ser trabajados directamente, tal como se obtienen del estudio estadístico, o pueden organizarse en grupos de igual frecuencia, facilitando el análisis.

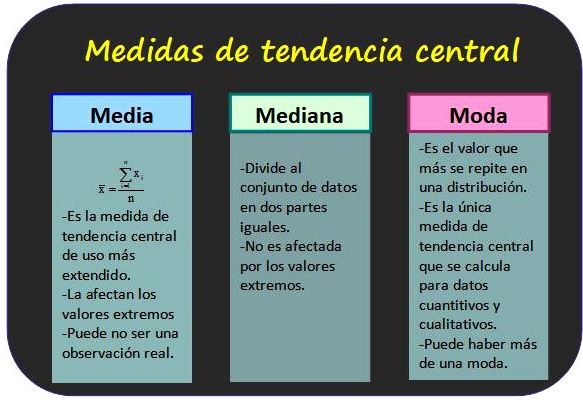
Medidas de tendencia central

Permiten conocer alrededor de qué valores se agrupan los datos estadísticos.

Media aritmética

También se conoce como el promedio de los valores de una variable y se obtiene sumando todos los valores y dividiendo el resultado por el número total de datos.

• Media aritmética para datos sin agrupar

Sea una variable  x de la cual se tienen n datos sin organizar o agrupar, su media aritmética se calcula así:

Y en notación de sumatoria:

Ejemplo

Los propietarios de un parador turístico de montaña tienen la intención de conocer cuántos días en promedio permanecen los visitantes en las instalaciones. Para ello se llevó un  registro de los días de permanencia de 20 grupos de turistas, obteniéndose los siguientes datos:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

El promedio de días que se quedan los turistas es de:

• Media aritmética para datos agrupados

Si los datos de la variable están organizados en una tabla de frecuencias absolutas f_i y los centros de clase son  x₁, x₂, …, x_n, la media se calcula mediante:

En la notación de sumatoria:

Mediana

La mediana de un grupo de n  valores de la variable  x es el valor central del grupo, con tal de que los valores estén ordenados en forma creciente. De esta forma la mitad de todos los valores son menores que la moda y la otra mitad son mayores.

• Mediana de datos no agrupados

Se pueden presentar los siguientes casos:

-Número  n  de valores de la variable  x  impar: la mediana es el valor que está justo en medio del grupo de valores:

-Número  n  de valores de la variable  x par: en este caso la mediana se calcula como el promedio de los dos valores centrales del grupo de datos:

Ejemplo

Para hallar la mediana de los datos del parador turístico primero se ordenan de menor a mayor:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

El número de datos es par, por lo tanto hay dos datos centrales: X₁₀ y X₁₁ y como ambos valen 2, su promedio también.

Mediana = 2

• Mediana de datos agrupados

Se utiliza la siguiente fórmula:

Los símbolos en la fórmula significan:

-c: ancho del intervalo que contiene a la mediana

-B_M: frontera inferior de ese mismo intervalo

-f_m: número de observaciones que contiene el intervalo al que pertenece la mediana.

-n: total de datos.

-f_BM: cantidad de observaciones que hay antes del intervalo que contiene la mediana.

Moda

La moda para datos no agrupados es el valor con la mayor frecuencia, mientras que para los datos agrupados es la clase con la mayor frecuencia. Se considera a la moda como el dato o la clase más representativo de la distribución.

Dos características importantes de esta medida es que un conjunto de datos puede tener más de una moda, y la moda se puede determinar tanto para datos cuantitativos como para datos cualitativos.

Ejemplo

Continuando con los datos del parador turístico, el que más se repite es 1, por lo tanto, lo más usual es que los turistas permanezcan 1 día en el parador.

Medidas de dispersión

Las medidas de dispersión describen qué tan agrupados están los datos alrededor de las medidas centrales.

Rango

Se calcula restando el dato mayor y el dato menor. Si esta diferencia es grande, es señal de que los datos son dispersos, mientras que los valores pequeños indican que los datos se encuentran cercanos a la media.

Ejemplo

El rango para los datos del parador turístico es:

Rango = 5−1= 4

Varianza

• Varianza para datos no agrupados

Para hallar la varianza s² se  requiere conocer primero la media aritmética, luego se calcula la diferencia al cuadrado entre cada dato y la media, se suman todas y se divide entre el total de observaciones. A estas diferencias se las conoce como desviaciones.

La varianza, que siempre es positiva (o cero), indica qué tan alejadas están las observaciones de la media: si la varianza es elevada, los valores están más dispersos que cuando la varianza es pequeña.

Ejemplo

La varianza para los datos del parador turístico es:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

• Varianza para datos agrupados

Para hallar la varianza de un  conjunto de datos agrupados, se requieren: i) la media, ii) la frecuencia  f_i  que es el total de datos en cada clase y  iii) x_i  o valor de la clase:

La desviación estándar es la raíz cuadrada positiva de la varianza, por lo que tiene una ventaja sobre la varianza: viene en las mismas unidades que la variable bajo estudio y así se tiene una idea más directa de lo cerca o lejos que está la variable de la media.

• Desviación estándar para datos no agrupados

Se determina simplemente encontrando la raíz cuadrada de la varianza para datos no agrupados:

La desviación estándar para los datos del parador turístico es:

s=√(s²)=√1.95=1.40

• Desviación estándar para datos agrupados

Se calcula encontrando la raíz cuadrada de la varianza para datos agrupados:

Medidas de posición

Las medidas de posición dividen a un conjunto ordenado de datos en partes de igual tamaño. La mediana, además de ser una medida de tendencia central es también una medida de posición, ya que divide al conjunto en dos partes iguales. Pero se pueden obtener partes de menor tamaño con cuartiles, deciles y percentiles.

Cuartiles

Los cuartiles dividen al conjunto en cuatro partes iguales, cada una con un 25 % de los datos. Se denotan como Q₁, Q₂ y Q₃ y la mediana es el cuartil Q₂. De esta manera, el 25% de los datos está por debajo del cuartil Q₁, el 50% por debajo del cuartil Q₂ o mediana y el 75% bajo el cuartil Q₃.

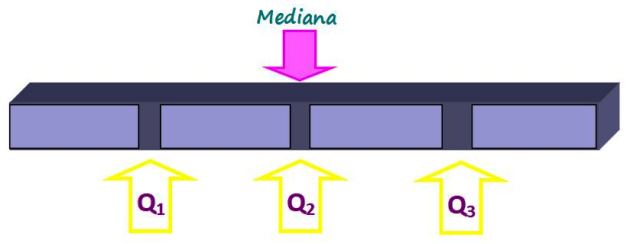
• Cuartiles para datos no agrupados

Se ordenan los datos y se divide el total en 4 grupos con igual número de datos cada uno. La posición del primer cuartil se halla mediante:

Q₁ =(n+1)/4

Siendo n el total de datos. Si el resultado es entero se ubica el dato correspondiente a esa posición, pero si  es decimal, se promedia el dato correspondiente a la parte entera con el siguiente, o para mayor precisión se interpola linealmente entre dichos datos.

Ejemplo

La posición del primer cuartil Q₁ para los datos del parador turístico es:

Q₁ =(n+1)/4 = (20+1) / 4 = 5.25

Esta es la posición del cuartil 1 y como el resultado es decimal, se buscan los datos X₅ y X_6, que son respectivamente X₅ = 1 y X₆ = 1 y se promedian, dando como resultado:

Primer cuartil =1

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

La posición del segundo cuartil Q₂ es:

Q₂ =2(n+1)/4 =10.5

Que es el promedio entre X₁₀ y X₁₁ y coincide con la mediana:

Segundo cuartil= Mediana= 2

La posición del tercer cuartil se calcula mediante:

Q₃ =3(n+1)/4 = 3(20+1) / 4 = 15.75

También es decimal, por lo tanto se promedian X₁₅ y X₁₆:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Pero como ambos valen 4:

Tercer cuartil = 4

La fórmula general para la posición de los cuartiles en datos no agrupados es:

Q_k =k(n+1)/4

Con k = 1,2,3.

• Cuartiles para datos agrupados

Se calculan de forma semejante a la mediana:

La explicación de los símbolos es:

-B_Q: frontera inferior del intervalo que contiene el cuartil

-c: ancho de ese intervalo

-f_q: cantidad de observaciones contenidas el intervalo del cuartil.

-n: total de datos.

-f_BQ: número de datos antes del intervalo que contiene el cuartil.

Deciles y percentiles

Los deciles y percentiles dividen el conjunto de datos en 10 partes iguales y 100 partes iguales respectivamente, y su cálculo se realiza de forma análoga al de los cuartiles.

• Deciles y percentiles para datos no agrupados

Se usan respectivamente las fórmulas:

D_k =k(n+1)/10

Con k = 1,2,3…9.

El decil D₅ debe ser igual a la mediana.

P_k =k(n+1)/100

Con k = 1,2,3…99.

El percentil P₅₀ debe ser igual a la mediana.

Ejemplo

En el ejemplo del parador turístico, la posición del D₃ es:

D₃ =3(20+1)/10 = 6.3

Como es un número decimal se promedian X₆ y X_7, ambos iguales a 1:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Significa que 3 décimas partes de los datos está por debajo de X₇ = 1 y las restantes por encima.

• Deciles y percentiles para datos agrupados

Las fórmulas son análogas a la de los cuartiles. Se usa la D para denotar los deciles y P para los percentiles y los símbolos se interpretan de forma semejante:

La regla empírica

Cuando los datos se distribuyen de forma simétrica y la distribución es unimodal, existe una regla llamada  regla empírica o regla 68 – 95 – 99, que los agrupa en los siguientes intervalos:

• 68% de los datos están en el intervalo:

• 95% de los datos están en el intervalo:

• 99% de los datos están en el intervalo:

Ejemplo

¿En qué intervalo se encuentra el 95% de los datos del parador turístico?

Se encuentran en el intervalo: [2.5−1.40 ; 2.5+1.40] = [1.1; 3.9].

Referencias

1. Berenson, M. 1985. Estadística para administración y economía. Interamericana S.A.
2. Devore, J. 2012. Probability and Statistics for Engineering and Science. 8th. Edition. Cengage.
3. Levin, R. 1988. Estadística para Administradores. 2da. Edición. Prentice Hall.
4. Spiegel, M. 2009. Estadística. Serie Schaum. 4 ta. Edición. McGraw Hill.
5. Walpole, R. 2007. Probabilidad y Estadística para Ingeniería y Ciencias. Pearson.