Desplazamiento angular: fórmula, cálculo, ejercicios
¿Qué es el desplazamiento angular?
El desplazamiento angular es el cambio o variación en la posición angular que experimenta un objeto en rotación, medido por lo general en radianes o cualquier otra medida dada para los giros, tales como los grados o las revoluciones.
Cuando un objeto gira alrededor de un eje fijo, su desplazamiento angular se determina midiendo el ángulo barrido por una línea que pasa por cualquier punto del cuerpo intersectando al eje de rotación, es decir, una línea radial.
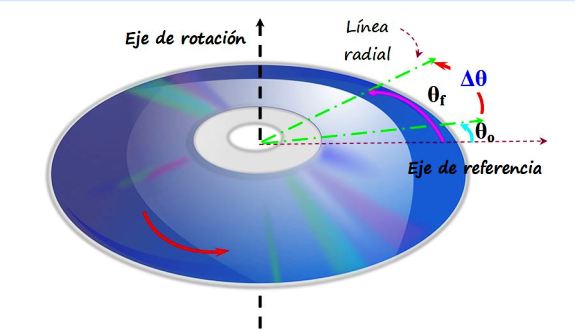
En la figura superior hay un CD que gira en sentido antihorario, siendo su eje de rotación el eje vertical. Sobre el plano del CD se coloca un eje de referencia, el cual corresponde al ángulo 0 radianes o 0 rad. La línea de color verde es una línea radial, que inicialmente se encuentra formando un ángulo θo con la referencia. Esta es su posición inicial.
Más tarde la línea verde se desplaza hacia una nueva posición llamada θf, y el desplazamiento experimentado, llamado Δθ es simplemente:
Δθ = θf − θo
Cualquier punto P del CD experimenta el mismo desplazamiento angular en un determinado intervalo de tiempo, excepto el centro, que es por donde pasa el eje de rotación y permanece en reposo.
Fórmulas y ecuaciones
Se tiene un objeto que gira en torno a un eje fijo O que sale de la pantalla hacia el lector. Y dentro de él, está el punto P, situado a una distancia r del eje de rotación y describiendo circunferencias de radio r.
Así se ve en la siguiente figura, que muestra un corte del objeto rotante, visto en sentido contrario al de las agujas del reloj. El punto en cuestión se encuentra en la posición angular θ, medida desde el eje de referencia, que en este caso es el eje horizontal.
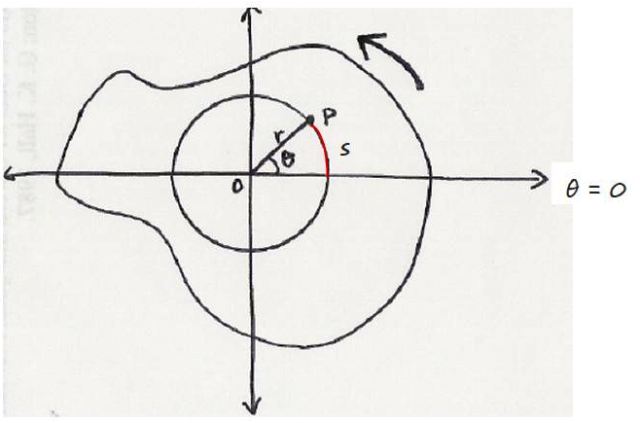
Por convención, a la rotación en sentido antihorario se le asigna sentido positivo, mientras que la rotación en sentido horario tiene signo negativo.
A medida que el punto P barre el ángulo θ, recorre simultáneamente el arco s. Como θ es un ángulo central, ya que su vértice ocupa el centro de la circunferencia, se cumple que:
Con θ expresado en radianes.
El desplazamiento angular es:
Δθ = θfinal − θinicial
Por ejemplo, si P partió de θinicial = 0 rad y después se encuentra en θfinal = 0.8 rad, su desplazamiento angular es de:
Δθ = 0.8 rad − 0 rad = 0.8 rad
Otros puntos del objeto pueden ocupar distintas posiciones angulares, pero todos experimentan el mismo desplazamiento angular. Sin embargo, las partículas más alejadas del centro recorren distancias mayores, ya que s = r⋅θ.
Medida de ángulos
En la rotación es frecuente encontrar los ángulos medidos en radianes, pero también se encuentran en grados y revoluciones o vueltas. En la resolución de problemas es necesario pasar de estas unidades a los radianes.
1 revolución equivale a un giro completo, es decir que cuando un punto rota una vuelta completa, ha girado 360 º y estos equivalen a 2π radianes, ya que en ese caso, el punto recorrió un arco igual a 2πr:
Pero simplificando, la equivalencia anterior se puede expresar así:
π radianes = 180º
¿Cómo se calcula el desplazamiento angular?
Se puede calcular el desplazamiento angular de forma análoga a como se calcula el desplazamiento en el movimiento en una dimensión, siguiendo un determinado modelo de movimiento. Para ello se define la velocidad angular media como el desplazamiento angular Δθ en un intervalo de tiempo dado Δt:
Donde la velocidad angular media se denota como ωm y viene dada en radianes/s en unidades del Sistema Internacional SI.
La velocidad angular instantánea es el límite de la velocidad angular media cuando Δt→0:
Es decir, es la primera derivada de la posición angular respecto al tiempo. A su vez, se puede definir una aceleración angular, denotada como α, que equivale a la derivada o tasa de cambio de la velocidad angular respecto al tiempo:
La cual también puede interpretarse como la segunda derivada de la posición angular respecto al tiempo.
Lo importante es que se pueden establecer dos modelos de movimiento en analogía con los movimientos rectilíneos, ya que aunque las rotaciones se llevan a cabo en el plano, basta una sola coordenada angular para establecer la posición de un punto cualquiera del objeto.
Movimiento circular uniforme
En el movimiento circular uniforme la velocidad angular es constante, esto es, la velocidad angular media es igual a la velocidad angular instantánea. Como la aceleración angular α es igual a 0, se puede escribir la siguiente ecuación para la posición en función del tiempo:
θ = θo + ωt
Donde θo es la posición inicial del móvil.
Movimiento circular uniformemente acelerado
En este caso, la aceleración angular α es constante, y en analogía con el movimiento rectilíneo uniformemente variado, se pueden escribir las siguientes ecuaciones:
- θ = θo + ωo t + ½ αt2
- ω = ωo + αt
- ω2 = ωo2 + 2α∙Δθ
Ejercicio resuelto
Primer ejercicio
Se puede suponer que la Tierra es un objeto rígido que gira sobre un eje fijo y que su rotación es casi uniforme. En el intervalo de tiempo Δt = 12 h hallar:
a) El desplazamiento angular de la Tierra
b) Su velocidad angular
c) La aceleración angular durante ese intervalo de tiempo.
Solución a
Sabiendo que en 24 horas la Tierra da una vuelta completa alrededor de su eje, en 12 horas habrá girado la mitad de una vuelta, es decir π radianes. Si se considera que parte de θinicial = 0 rad, entonces su desplazamiento angular es:
Δθ = π radianes
Solución b
Como la rotación es uniforme, la velocidad angular es el cociente entre el desplazamiento angular y el tiempo, además, 1 hora = 3600 s:
ω = π rad / 12 h = π rad / (12 x 3600) s= 0.000073 rad/s.
Solución c
La aceleración angular es nula, puesto que la rotación de la Tierra es uniforme.
Segundo ejercicio
Juan ha corrido una distancia de 35 metros sobre una pista de atletismo circular cuyo radio es igual a 7 metros. Calcule el desplazamiento angular que ha realizado Juan.
Solución
Ya que se conoce la distancia del arco recorrido y el radio de la circunferencia, se puede aplicar la segunda fórmula para conocer el desplazamiento angular hecho por Juan. Utilizando la fórmula descrita arriba se tiene que θ=35/7 = 5 radianes.
Tercer ejercicio
Si se tiene que Mario ha recorrido en su vehículo la mitad de una pista de carreras circular, ¿cuál es el desplazamiento angular que ha hecho Mario?
Solución
En este ejercicio se aplicará la primera fórmula. Ya que se conoce que Mario ha recorrido la mitad de la pista, se puede suponer que él inició la carrera en el ángulo 0° y al llegar a la mitad de la circunferencia ha recorrido 180°. Por lo tanto, la respuesta es 180°-0°=180°=π radianes.
Cuarto ejercicio
María tiene una piscina de forma circular. Su perro corre alrededor de la piscina recorriendo una distancia de 18 metros. Si el radio de la piscina es de 3 metros, ¿cuál es el desplazamiento angular realizado por la mascota de María?
Solución
Ya que la piscina es circular y se conoce el radio de la misma, se puede proceder a utilizar la segunda fórmula.
Se sabe que el radio es igual a 3 metros, y la distancia recorrida por la mascota es igual a 18 metros. Por lo tanto, el desplazamiento angular realizado es igual a θ = 18 / 3 = 6 radianes.
Referencias
- Katz, D. 2013. Physics for Scientists and Engineers. Foundations and Connections. Cengage Learning.
- Rex, A. 2011. Fundamentos de Física. Pearson.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1. Pearson.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning.
- Tipler, P. (2006). Física para la Ciencia y la Tecnología. 5ta Ed. Volumen 1. Editorial Reverté.
