Ángulos alternos externos: ejercicios y ejercicios resueltos
Los ángulos alternos externos son los ángulos que se forman cuando son interceptadas dos rectas paralelas con una recta secante. Además de estos ángulos se forman otro par que son llamados ángulos alternos internos.
La diferencia entre estos dos conceptos son las palabras “externos” e “internos” y tal cual como el nombre lo indica, los ángulos alternos externos son los que se forman en el exterior de las dos rectas paralelas.
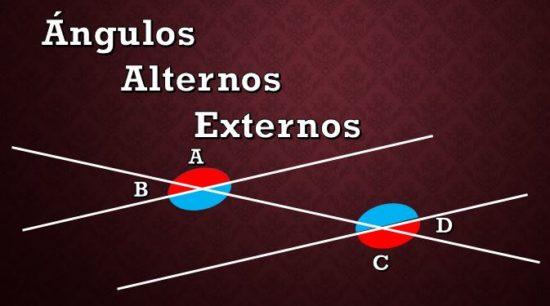
Como se aprecia en la imagen anterior, hay ocho ángulos formados entre las dos rectas paralelas y la recta secante. Los ángulos de color rojo son los alternos externos, y los ángulos azules son los ángulos alternos internos.
Índice del artículo
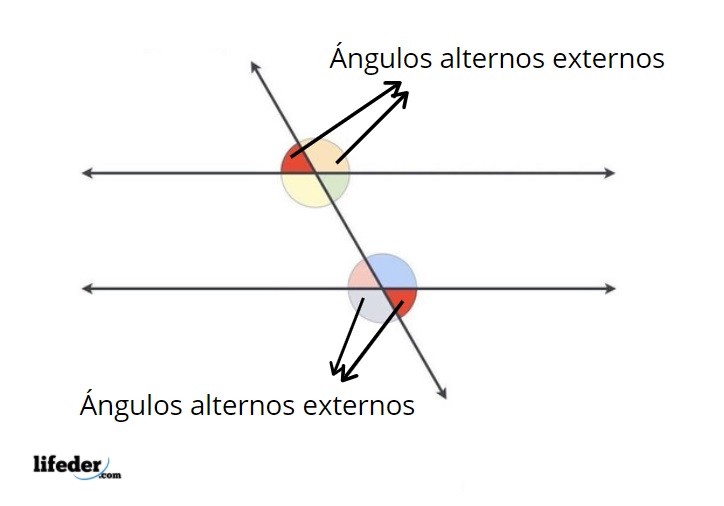
En la introducción ya se explicó cuáles son los ángulos alternos externos. Además de ser los ángulos externos entre las paralelas, estos ángulos cumplen otra condición.
La condición que cumplen es que los ángulos alternos externos que se forman sobre una recta paralela son congruentes; tiene la misma medida que los otros dos que se forman sobre la otra recta paralela.
Pero cada ángulo alterno externo es congruente con el que está del otro lado de la recta secante.
Si se observa la imagen del inicio y la explicación anterior, se puede concluir que los ángulos alternos externos que son congruentes entre sí son: los ángulos A y C, y los ángulos B y D.
Para demostrar que son congruentes se deben utilizar propiedades de ángulos como: ángulos opuestos por el vértice y ángulos alternos internos.
A continuación se presentan una serie de ejercicios donde debe aplicarse la definición y propiedad de congruencia de los ángulos alternos externos.
En la siguiente imagen, ¿cuál es la medida del ángulo A sabiendo que el ángulo E mide 47°?
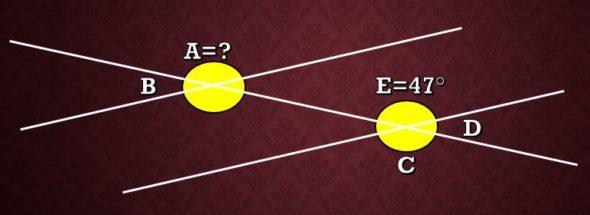
Solución
Como se explicó antes, los ángulos A y C son congruentes por ser alternos externos. Por lo tanto, la medida de A es igual a la medida de C. Ahora, ya que los ángulos E y C son ángulos opuestos por el vértice, se tiene que estos tienen la misma medida, por lo tanto, la medida de C es 47°.
En conclusión, la medida de A es igual a 47°.
Calcule la medida del ángulo C que se muestra en la siguiente imagen, sabiendo que el ángulo B mide 30°.
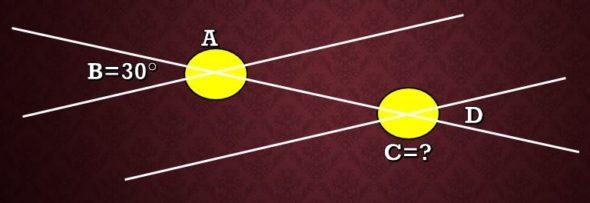
Solución
En este ejemplo, se usa la definición ángulos suplementarios. Dos ángulos son suplementarios si la suma de sus medidas es igual a 180°.
En la imagen se aprecia que A y B son suplementarios, por lo tanto A+B=180°, es decir, A+30°=180° y por lo tanto A=150°. Ahora, como A y C son ángulos alternos externos, entonces sus medidas son las mismas. Por lo tanto, la medida de C es 150°.
En la imagen siguiente, se tiene que la medida del ángulo A es 145°. ¿Cuál es la medida del ángulo E?
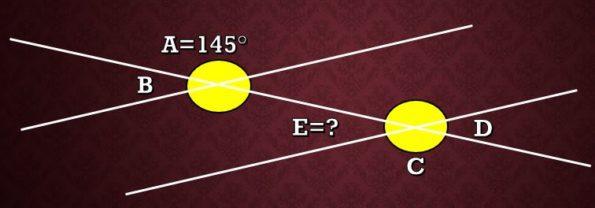
Solución
En la imagen se aprecia que los ángulos A y C son ángulos alternos externos, por lo tanto, estos tienen la misma medida. Es decir que la medida de C es 145°.
Como los ángulos C y E son ángulos suplementarios, se tiene que C+E=180°, es decir 145°+E=180° y por lo tanto la medida del ángulo E es 35°.
- Bourke. (2007). An Angle on Geometry Math Workbook. NewPath Learning.
- C. E. A. (2003). Elementos de geometría: con numerosos ejercicios y geometría del compás. Universidad De Medellin.
- Clemens, S. R., O’Daffer, P. G., & Cooney, T. J. (1998). Geometría. Pearson Educación.
- Lang, S., & Murrow, G. (1988). Geometry: A High School Course. Springer Science & Business Media.
- Lira, A., Jaime, P., Chavez, M., Gallegos, M., & Rodríguez, C. (2006). Geometria y Trigonometria. Ediciones Umbral.
- Moyano, A. R., Saro, A. R., & Ruiz, R. M. (2007). Álgebra y Geometría Cuadrática. Netbiblo.
- Palmer, C. I., & Bibb, S. F. (1979). Matemáticas prácticas: aritmética, álgebra, geometría, trigonometría y regla de cálculo. Reverte.
- Sullivan, M. (1997). Trigonometría y geometría analítica. Pearson Educación.
- Wingard-Nelson, R. (2012). Geometry. Enslow Publishers, Inc.
