Sucesión compuesta: qué es, explicación, ejemplos y ejercicios
¿Qué es una sucesión compuesta?
Una sucesión compuesta consiste en una secuencia de elementos, creada a partir de dos (o más) sucesiones distintas y alternadas. Cada una de estas sucesiones tiene una regla particular, que se usa para encontrar sus respectivos elementos.
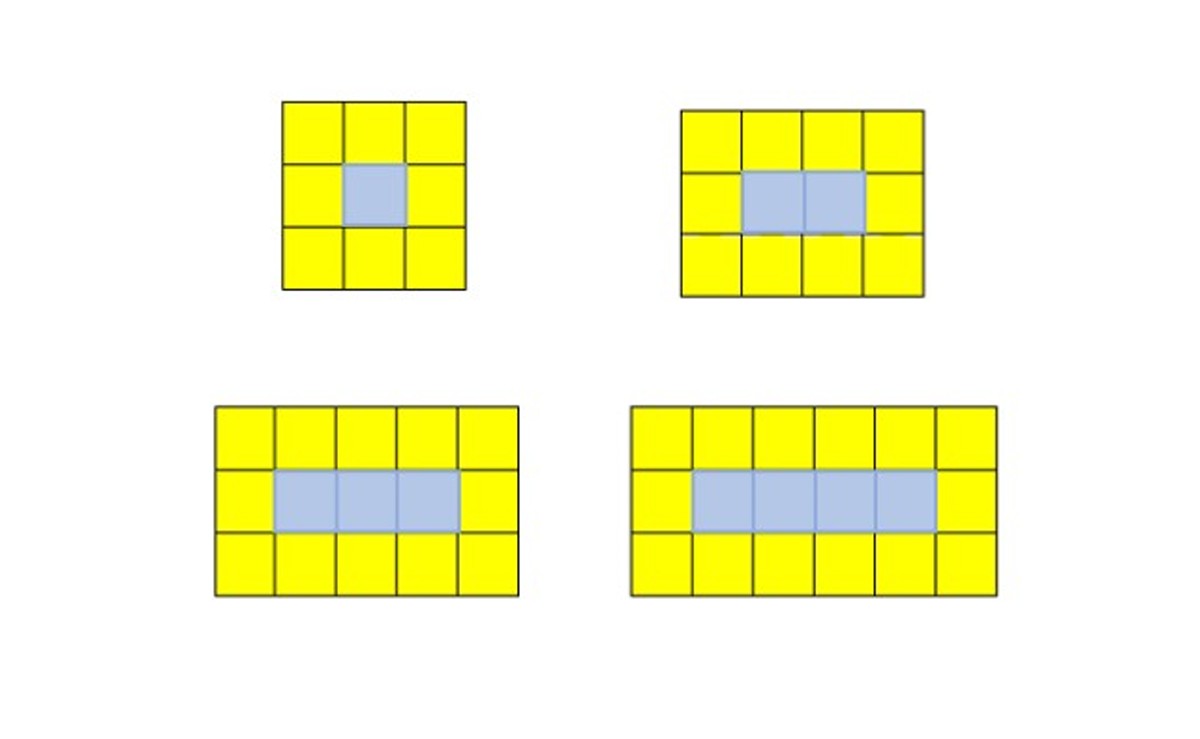
Los elementos no tienen que ser numéricos, pudiendo ser figuras, símbolos o letras, pero las que son a base de números se llaman sucesiones aritméticas. La figura con la que comienza nuestro artículo muestra una sucesión compuesta a partir de cuadrados amarillos y azules.
En esta sucesión, se parte de un cuadrado grande que consta de 8 cuadrados amarillos y un cuadrado azul. Para conseguir el siguiente término, se añade un cuadrado amarillo a la izquierda o a la derecha de la primera y la tercera fila de cuadrados. El espacio que resulta en la fila central, se llena con un cuadrado azul.
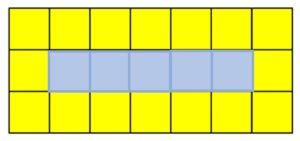
Cada figura en la secuencia recibe el nombre de término. Si se quiere encontrar el quinto término, hay que añadir un cuadrado amarillo a la derecha de las filas primera y tercera, y un cuadrado azul en la fila segunda:
Explicación
En las sucesiones compuestas, los términos se obtienen alternando los términos de dos o más sucesiones simples independientes. Para comprender mejor la idea, conviene repasar los detalles de una sucesión simple.
Por ejemplo, la siguiente sucesión simple consta de los números naturales pares:
2, 4, 6, 8, 10, 12 …
Los puntos suspensivos indican que la sucesión tiene infinitos términos.
Cada uno de los términos se denota mediante una letra minúscula y un número, a modo de subíndice. Este número señala la posición o índice de cada término. En la sucesión anterior, se puede escribir:
a1 = 2; a2 = 4; a3 = 6; a4 = 8 …
Es muy conveniente tener una forma para calcular cualquier término que se desee de la sucesión, es decir, su regla particular. Con ella se calcula el término n-ésimo, o término general, denotado como an.
Continuando con el ejemplo de la sucesión de números pares, se puede establecer la forma de calcular el término n-ésimo, a partir del término anterior:
an = an–1 + 2
Donde an–1 es el término que precede a an.
Claro que sería mejor conocer el término general sin depender de otros términos. En esta sucesión es fácil notar que un término cualquiera se encuentra multiplicando por 2 la posición que ocupa, dada el subíndice del término. De esta forma se escribe:
an = 2n
Los antiguos griegos ya conocían las sucesiones de números pares e impares. La sucesión de números naturales impares, por su parte, se puede escribir como:
1, 3, 5, 7, 9, 11…
Y combinando la sucesión de los números pares con la de los impares, resulta la sucesión compuesta siguiente:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12…
Cuyo resultado es el conjunto de los números naturales.
Términos de una sucesión compuesta
Puede resultar divertido tratar de encontrar la relación que existe en una secuencia de números, para lo cual hay que observarla cuidadosamente y tratar de identificar si se trata de una sucesión compuesta.
La forma general de una sucesión compuesta de dos sucesiones será:
a1, b1, a2, b2, a3, b3, a4, b4, …
Donde a1, a2, a3, a4, … son los términos de la primera sucesión y b1, b2, b3, b4, … los de la segunda. Siempre van intercalados, como ocurre en este ejemplo:
7, 8, 14, 16, 21, 24, 28, 32, 35…
¿Cuál será el término que sigue?
Para saberlo, sepárese la sucesión en dos conjuntos alternados de números, del siguiente modo:
- 7, 14, 21, 28, 35 …
- 8, 16, 24, 32 …
En el primero de estos conjuntos, aparecen los múltiplos del 7:
a1 = 7 × 1 = 7; a2 = 7 × 2 = 14; a3 = 7 × 3 = 21; a4 = 7 × 4 = 28; a5 = 7 × 5 = 35
El término general de esta sucesión es:
an = 7n
Y en el segundo, se trata de los múltiplos de 8:
b1 = 8 × 1 = 8; b2 = 8 × 2 = 16; b3 = 8 × 3 = 24; b4 = 8 × 4 = 32
Por lo que su término general es:
bn = 8n
Regresando a la sucesión compuesta original, el 35 pertenece a la primera secuencia, cuyos términos son a1, a2, a3, a4 … El 35 es el quinto término, por lo que el término que sigue tiene que ser b5, el cual se obtiene fácilmente de la regla para hallar el término general:
b5 = 8 × 5 = 40
Y se escribe:
7, 8, 14, 16, 21, 24, 28, 32, 35, 40…
Ejemplos de sucesiones compuestas
Ejemplo 1
Se puede crear una sucesión compuesta con figuras geométricas, como el cuadrado y el círculo, disponiéndolos como se muestra seguidamente:
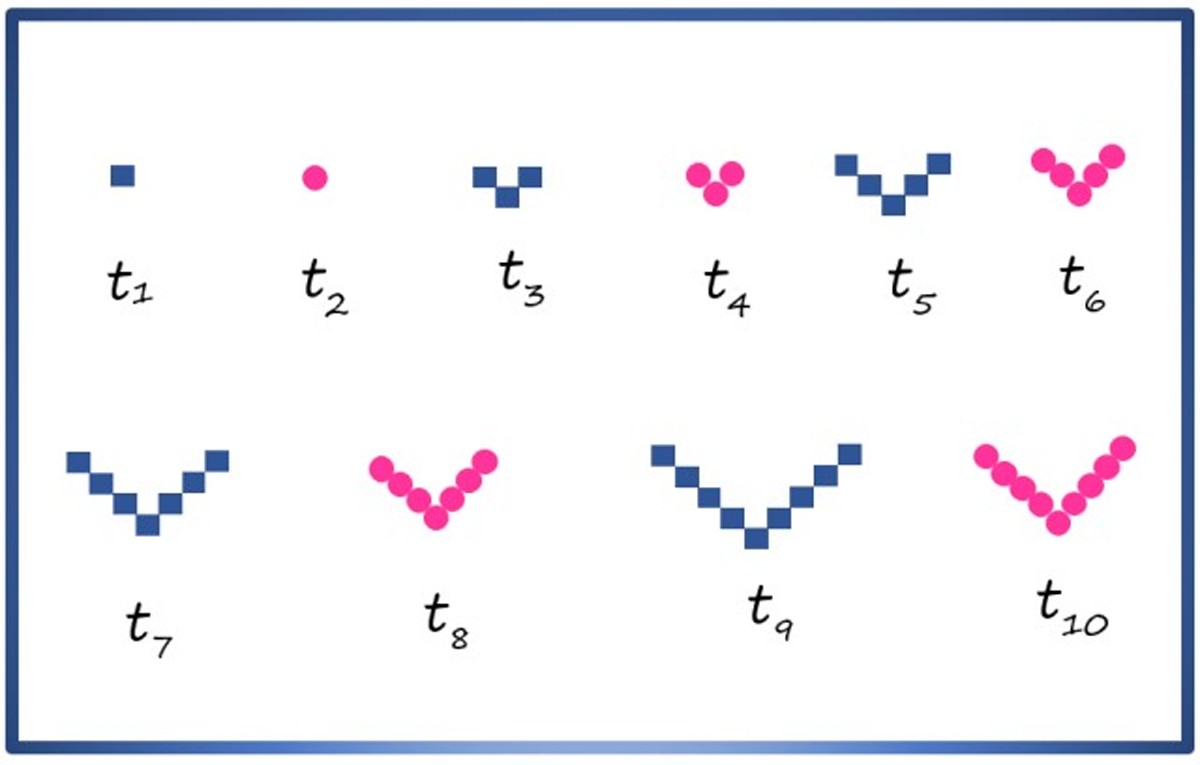
Cada término se denota mediante t1, t2, t3, t4 …, los términos de índice par constan de círculos y los de índice impar, de cuadrados. Observando cuidadosamente la secuencia es posible saber, por ejemplo, que el término t11, que no aparece en la imagen, consta de 11 cuadrados con la disposición en V.
Ejemplo 2
La siguiente sucesión compuesta consta de símbolos, en este caso, las letras R y S:
R SS RR SSS RRR SSSS RRRR SSSSS RRRRR SSSSSSS …
Cada nuevo término se construye añadiendo una letra al anterior. Los primeros cuatro términos de la secuencia mostrada son:
t1= R ; t2= SS ; t3= RR ; t4= SSS …
Y el siguiente término que aparecería luego de los términos mostrados es:
t11= RRRRRR
Ejemplo 3
Los ejemplos anteriores mostraron sucesiones ascendentes, en los que cada valor aumenta, de alguna manera, respecto al anterior. Pero no siempre tiene que ser de esta forma, ya que las sucesiones pueden ser descendentes, es decir, que tengan algún patrón de disminución.
Y se pueden combinar sucesiones ascendentes con sucesiones descendentes.
La siguiente sucesión numérica es compuesta:
4, 36, 7, 35, 10, ___, ___, 33, 16, ___, ___, …
Se la puede separar en dos sucesiones:
- 4, 7, 10, ___,16, ___, …
- 36, 35, ___, 33, ___, …
¿Cuáles son los valores que se deben colocar en los espacios en blanco?
Observando con cuidado la primera sucesión, cada término se obtiene sumando 3 al término precedente. Se trata, pues, de una sucesión ascendente:
7 = 4 + 3
10 = 7 + 3
Por lo tanto, en el primer espacio en blanco hay que colocar:
10 + 3 = 13
Tras esto, el siguiente término es, en efecto:
16 = 13 + 3
Y el que va en el segundo espacio en blanco es:
16 + 3 = 19
La segunda sucesión es descendente y es muy fácil hallar los términos que faltan, pues se observa que cada término se obtiene restando 1 del término anterior, por lo tanto:
36, 35, 34, 33, 32 …
Finalmente, se puede escribir:
4, 36, 7, 35, 10, 34, 13, 33, 16, 32, 19, …
Ejercicios resueltos
Ejercicio 1
En la sucesión compuesta del ejemplo 3 en la sección precedente:
a) ¿Pertenece el 29 a dicha sucesión?
b) Escribir 10 términos más de esta sucesión
Respuesta a
Sí pertenece, ya que la segunda sucesión es descendente y sus términos se obtienen restando 1 del término anterior. De esta forma, eventualmente se llega al 29.
Respuesta b
4, 36, 7, 35, 10, 34, 13, 33, 16, 32, 19, 31, 22, 30, 25, 29, 28, 28, 31, 27, 34, …
Obsérvese que algunos términos se repiten.
Ejercicio 2
Hallar los términos faltantes en la siguiente sucesión compuesta:
100, 500, 115, 480, 130, 460, 145, 440, 160, 420, …
Respuesta
Se escriben los términos impares para obtener la primera sucesión:
100, 115, 130, 145, 160, …
Se observa que, para hallar cada término, hay que sumarle 15 al término anterior, por lo tanto, el término que sigue al 160 es 175.
La segunda sucesión consiste en:
500, 480, 460, 440, 420, …
Cada término difiere del anterior en 20, siendo descendente la sucesión, por lo tanto, el término que sigue a 420 es 400.
Con esta información, a la sucesión compuesta original se le añaden dos términos más, así:
100, 500, 115, 480, 130, 460, 145, 440, 160, 420, 175, 400, …
Referencias
- Larson, R. (2012). Precálculo. 8va. Edición. Cengage Learning.
- Stewart, J. (2007). Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
- Sucesiones compuestas. Recuperado de: media.educacioncampeche.gob.mx.
- Sucesiones numéricas. Recuperado de: matemathweb.com.
- Sucesiones. Progresiones aritméticas y geométricas. Recuperado de: macmillaneducation.es.
