Derivada de cotangente: cálculo, demostración, ejercicios
La derivada de la cotangente es igual al opuesto del cuadrado de la cosecante “-Csc2”. Esta fórmula obedece a las leyes de derivada por definición y a la diferenciación de funciones trigonométricas. Se denota de la siguiente manera:
d ( ctg u ) = -csc2 u . du
Donde “du” simboliza la expresión derivada de la función argumento, con respecto a la variable independiente.

Índice del artículo
- 1 ¿Cómo se calcula?
- 2 Características de la función cotangente
- 3 Demostración
- 4 Ejercicios resueltos
- 5 Referencias
El procedimiento para desarrollar estas derivadas es bastante simple. Basta tan solo con identificar correctamente el argumento y el tipo de función que representa.
Por ejemplo, la expresión Ctg ( f/g ) presenta una división en su argumento. Esto hará necesaria una diferenciación referente a U/V, después de desarrollar la derivada de la cotangente.
La cotangente es la función recíproca de la tangente. Algebraicamente esto quiere decir que:
(1/tg x) = ctg x
Ctg x = Cos x / Sen x
Es incorrecto decir que la función cotangente es la “inversa” de la tangente. Esto se debe a que la función inversa de la tangente por definición es arco tangente.
( Tg-1 x ) = arctg x
Según la trigonometría pitagórica, la cotangente está involucrada en los siguientes apartados:
Ctg x = ( cos x ) / ( sen x )
Ctg2 x + 1 = Csc2 x
De acuerdo a la trigonometría analítica responde a las siguientes identidades:
Ctg ( a + b ) = ( 1 – tg a . tg b ) / ( tg a + tg b )
Ctg ( a – b ) = ( 1 + tg a . tg b ) / ( tg a – tg b )
Ctg (2a) = ( 1 – tg2 a ) / ( 2tg a )
Es necesario analizar diversas características de la función f (x) = ctg x para poder definir los aspectos necesarios para estudiar su diferenciabilidad y aplicación.
La función cotangente no está definida en los valores que hacen cero a la expresión “Senx”. Debido a su equivalente Ctg x = ( cos x ) / ( sen x ), tendrá una indeterminación en todos los “nπ” con n perteneciente a los enteros.
Es decir, que en cada uno de estos valores de x = nπ existirá una asíntota vertical. Al acercarse por la izquierda el valor de la cotangente disminuirá rápidamente, y al acercarse por la derecha, la función aumentará indefinidamente.
El dominio de la función cotangente está expresado por el conjunto { x ∈ R / x ≠ nπ, n ∈ Z }. Este se lee como “x que pertenece al conjunto de los números reales tal que, x es diferente de nπ, con n perteneciente al conjunto de los números enteros”.
El rango de la función cotangente abarca desde menos hasta más infinito. Por eso se puede concluir que su rango es el conjunto de los números reales R.
La función cotangente es periódica y su periodo es igual a π. De esta forma se cumple la igualdad Ctg x = Ctg ( x + nπ ), donde n pertenece a Z.
Es una función impar, ya que Ctg (-x) = – Ctg x. De esta forma se sabe que la función presenta una simetría con respecto al origen coordenado. También presenta un decrecimiento en todo intervalo ubicado entre 2 asíntotas verticales sucesivas.
No posee valores máximos ni mínimos, debido a que sus aproximaciones a las asíntotas verticales presentan comportamientos donde la función crece o decrece de manera indefinida.
Los ceros o raíces de la función cotangente se encuentran en los múltiplos impares de π/2. Esto quiere decir que se cumple Ctg x = 0 en los valores de la forma x = nπ/2 con n entero impar.
Existen 2 formas de demostrar la derivada de la función cotangente.
Se demuestra la derivada de la función cotangente desde su equivalente en senos y cosenos.
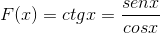
Se trata como la derivada de una división de funciones
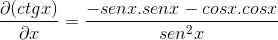
Después de derivar se agrupan los factores y se busca emular las identidades pitagóricas
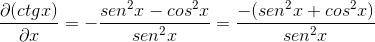
Sustituyendo las identidades y aplicando reciprocidad se obtiene la expresión
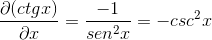
La siguiente expresión corresponde a la derivada por definición. Donde se acerca a cero la distancia entre 2 puntos de la función.
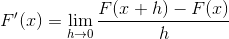
Sustituyendo para la cotangente se tiene que:
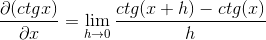
Se aplican identidades para la suma de argumentos y reciprocidad
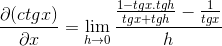
Se opera de manera tradicional la fracción del numerador
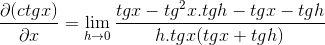
Eliminando los elementos opuestos y sacando factor común se obtiene
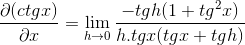
Aplicando identidades pitagóricas y reciprocidad se tiene que
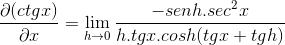
Los elementos evaluados en x son constantes respecto del límite, por tanto pueden salir del argumento de este. Luego se aplican propiedades de límites trigonométricos.
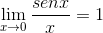
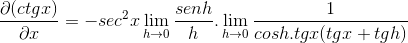
El límite es evaluado
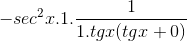
Luego se factoriza hasta llegar al valor deseado
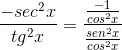
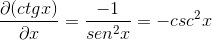
Queda demostrada así la derivada de la cotangente como el opuesto del cuadrado de la cosecante.
Según la función f (x), defina la expresión f’(x)
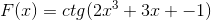
Se aplica la derivación correspondiente respetando la regla de la cadena
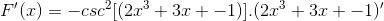
Derivando el argumento
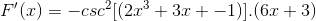
En ocasiones es necesario aplicar identidades reciprocas o trigonométricas para adecuar las soluciones.
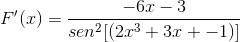
Defina la expresión diferencial correspondiente a F (x)
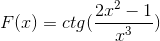
Según la fórmula de derivación y respetando la regla de la cadena
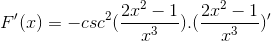
Se procede a derivar el argumento, mientras el resto permanece igual
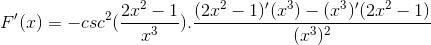
Derivando la totalidad de los elementos
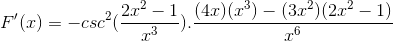
Operando de manera tradicional los productos de igual base
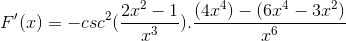
Se suman los elementos iguales y se extrae el factor común
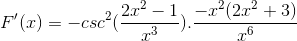
Se simplifican y operan los signos. Dando paso a la expresión completamente derivada
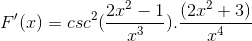
- Trigonometric Series, Volumen 1. A. Zygmund. Cambridge University Press, 2002
- Calculus of a Single Variable. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 nov. 2008
- Calculus with trigonometry and analytic geometry. John H. Saxon, John Saxon, Frank Wang, Diana Harvey. Saxon Publishers, 1988
- Multivariable Analysis. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 dic. 2010
- System Dynamics: Modeling, Simulation, and Control of Mechatronic Systems. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 mar. 2012
- Calculus: Mathematics and Modeling. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 ene. 1999
