Icoságono: qué es, lados, área, ángulos, perímetro

¿Qué es un icoságono?
Un icoságono o isodecágono es un polígono que tiene 20 lados. Un polígono es una figura plana formada por una secuencia finita de segmentos de recta (más de dos), los cuales encierran una región del plano.
A cada segmento de recta se le llama lado y a la intersección de cada par de lados se le llama vértice. De acuerdo al número de lados, los polígonos reciben nombres particulares.
Los más comunes son el triángulo, cuadrilátero, pentágono y hexágono, los cuales tienen 3, 4, 5 y 6 lados respectivamente, pero pueden construirse con el número de lados que se desee.
Características de un icoságono
A continuación se presentan algunas características de los polígonos y su aplicación en un icoságono.
1- Clasificación
Un icoságono, al ser un polígono, puede clasificarse en regular e irregular, donde la palabra regular hace referencia a que todos los lados tienen la misma longitud y los ángulos interiores miden todos lo mismo; en caso contrario se dice que el icoságono (polígono) es irregular.
2- Isodecágono
Al icoságono regular se le llama también isodecágono regular, pues para obtener un icoságono regular lo que se debe hacer es bisecar (dividir en dos partes iguales) cada lado de un decágono regular (polígono de 10 lados).
3- Perímetro
Para calcular el perímetro “P” de un polígono regular se multiplica el número de lados por la longitud de cada lado.
En el caso particular de un icoságono, se tiene que el perímetro es igual a 20xL, donde “L” es la longitud de cada lado.
Por ejemplo, si se tiene un icoságono regular de lado 3 cm, su perímetro es igual a 20x3cm=60 cm.
Es claro que, si el isocágono es irregular, la fórmula anterior no se puede aplicar.
En ese caso, se deben sumar por separado los 20 lados para obtener el perímetro, es decir, el perímetro “P” es igual a ∑Li, con i=1,2,…,20.
4- Diagonales
El número de diagonales “D” que posee un polígono es igual a n(n-3)/2, donde n representa el número de lados.
En el caso de un icoságono se tiene que este tiene D=20x(17)/2=170 diagonales.
5- Suma de los ángulos internos
Existe una fórmula que ayuda a calcular la suma de los ángulos internos de un polígono regular, la cual se puede aplicar a un icoságono regular.
La fórmula consiste en restarle 2 al número de lados del polígono y luego multiplicar este número por 180º.
La forma cómo se obtiene esta fórmula es que podemos dividir un polígono de n lados en n-2 triángulos, y usando el hecho de que la suma de los ángulos internos de un triángulo es 180º se obtiene la fórmula.
En la siguiente imagen, se ilustra la fórmula para un eneágono regular (polígono de 9 lados).
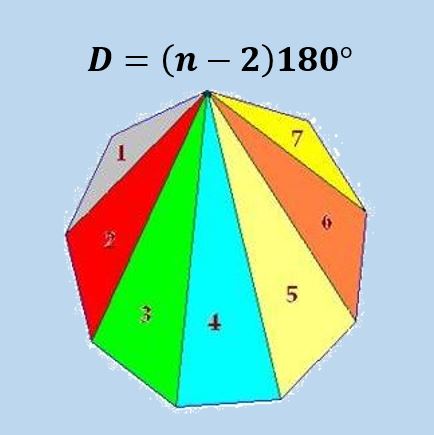
Usando la fórmula anterior se obtiene que la suma de los ángulos internos de cualquier icoságono es 18×180º=3240º o 18π.
6- Área
Para calcular el área de un polígono regular es muy util conocer el concepto de apotema. El apotema es una recta perpendicular que va desde el centro del polígono regular hasta el punto medio de cualquiera de sus lados.
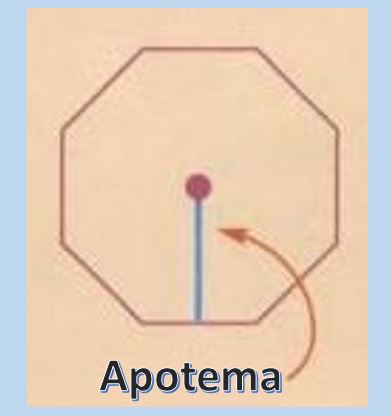
Una vez que se conoce la longitud del apotema, el área de un polígono regular es A=Pxa/2, donde “P” representa el perímetro y “a” el apotema.
En el caso de un icoságono regular se tiene que su área es A=20xLxa/2=10xLxa, donde “L” es la longitud de cada lado y “a” su apotema.
Por otro lado, si se tiene un polígono irregular de n lados, para calcular su área, se divide el polígono en n-2 triángulos conocidos, luego se calcula el área de cada uno de estos n-2 triángulos y finalmente se suman todas estas áreas.
El método descrito anteriormente se conoce como triangulación de un polígono.
Referencias
- Elementos de geometría: con numerosos ejercicios y geometría del compás. Universidad De Medellin.
- IGER. (s.f.). Matemática Primer Semestre Tacaná. IGER.
