¿Cómo sacar el porcentaje? ejemplos y ejercicios
Se puede sacar un porcentaje con varios métodos. Se puede calcular rápidamente el 10% de cualquier número solamente al mover su coma decimal una posición hacia la izquierda. Por ejemplo, el 10% de 100 es 10; el 10% de 1000 es 100.
Si se quieren calcular porcentajes más complejos como el 36% de 25 o el 250% de 20, se necesitan usar otros métodos. Para los casos en los que el sistema del 10% no es aplicable, se pueden tener en cuenta las siguientes metodologías.

El término porcentaje significa cierta parte de cada cien y se refiere a la operación aritmética que se lleva a cabo para encontrar dicha parte. Por ejemplo 20% (se lee “veinte por ciento”) de descuento en pesos significa que por cada 100 pesos se descuentan 20 pesos.
El porcentaje sirve para calcular qué parte del total representa una cantidad. En este caso, el total se lleva a la escala de 100 y el porcentaje informa qué cantidad, en base a esos 100, es la parte que se ha de calcular.
Veamos cómo se hace con estos ejemplos. En primer lugar lo hacemos en forma de fracción:
- 20% = 20/100
- 5% = 5 /100
- 0,7% = 0,7 / 100
- 100% = 100 / 100
Obsérvese que el 100% es igual a 1. Pero los porcentajes también pueden escribirse en forma decimal:
- 20% = 0,20
- 5% = 0,05
- 0,7% = 0,007
- 100% = 1,0
Cuando se expresa el porcentaje de cierto número en forma decimal, simplemente se desplaza la coma de ese número dos lugares a la izquierda. En el porcentaje también se aplica la regla de la proporcionalidad:
20% es 20 de cada 100, por lo tanto:
El 20% de 100 es 20, el 20% de 200 es 40, el 20% de 300 es 60, el 20% de 50 es 10.
Regla general para el 20 % de cualquier cantidad
20% de X es X *(20 / 100) = X * 0,2 = 0,2*X
Esta regla se puede extender fácilmente para encontrar cualquier otro porcentaje que se desee. Veamos cómo en el siguiente apartado.
Ejercicio resuelto con fórmula para calcular el n%
Una fórmula para resumir lo antes explicado y calcular rápidamente cualquier porcentaje n es:
n % =(A * n)/100
Por ejemplo se desea calcular el 25% de 400
Entonces n = 25 y A = 400, lo que resulta en (400*25)/100 = 100
Ejemplo
¿Qué porcentaje de 60 es 24?
Solución
Lo que se pide es equivalente a preguntar ¿cual es el n% de 60 que da 24?
Planteamos la fórmula general:
60 * n / 100 = 24
Despejamos n con este procedimiento:
-El 100 que está dividiendo en el miembro izquierdo de la igualdad, pasa al miembro derecho multiplicando.
-Y el 60 que multiplica en el miembro izquierdo pasa al miembro derecho dividiendo.
n = 24 *100 / 60 = 2400 / 60 = 240 / 6 = 6 *40 / 6 = 40
Se concluye que el 40% de 60 es 24.
Ejercicios resueltos de cálculo de porcentaje
A continuación se muestran ejercicios sencillos para comenzar a practicar lo antes dicho.
Ejercicio 1
Hallar el 50% de 90.
Solución
Aquí X = 90, n = 50 % y sustituimos:
90 * 50% = 90 * (50 / 100) = 4500 /100 = 45
Este es bastante simple, porque el 50 % de cualquier cantidad es la mitad de dicha cantidad y la mitad de 90 es 45.
Ejercicio 2
Hallar el 30% de 90.
Solución
90 * 30% = 90 * (30 / 100) = 2700 /100 = 27
Aumentos porcentuales
Es frecuente en la vida cotidiana escuchar sobre el aumento de algo, por ejemplo un aumento en la producción, un incremento salarial o la subida de un producto. Casi siempre se expresa en forma porcentual.
Por ejemplo, cierto producto costaba 300€ pero sufrió un incremento del 30%. Nos preguntamos: ¿cuál es el nuevo precio del producto?
Lo primero es calcular la porción que corresponde al aumento. Como el aumento es de 30 partes de 100, entonces la porción de aumento, en base al precio original de 300, es tres veces las 30 partes, es decir 3*30 = 90.
El producto aumentó 90€, por lo que el nuevo precio final será lo que costaba antes más el aumento:
Precio nuevo = precio viejo + 90€ = 390€
Podemos construir una fórmula para el cálculo del aumento porcentual. Utilizamos letras para simbolizar los precios, así:
–f es el valor final
-i es el valor inicial y
-n es el porcentaje de aumento.
Con estos nombres, el valor final se calcularía así:
f = i + (i* n / 100)
Pero como i está repetido en ambos términos, se puede sacar como factor comúnpara obtener esta otra expresión, igualmente válida:
f = i * ( 1 + n / 100)
Verifiquemos con el caso ya resuelto, el producto que costaba 300€ y aumentó 30%. Así nos aseguramos de que la fórmula funciona bien:
Precio final = f = 300€ * ( 1 + 30/100) = 300€ *( 1 + 0,3) = 300€ * 1,3 = 390€
Ejercicio 3
Un empleado ganaba 1500€, pero fue ascendido y su salario tuvo un aumento de 20%. ¿Cuál es su nuevo sueldo?
Solución
Apliquemos la fórmula:
f = 1500€ * (1 + 20 /100) = 1500€ * (1 + 0,2) = 1500€ * 1,2 = 1800€
El nuevo salario del empleado es 1800€.
Disminuciones porcentuales
En el caso de disminuciones, la fórmula para el cálculo del valor final f de cierta cantidad inicial i que sufrió una disminución de n% es:
f = i * ( 1 – n / 100)
Debe notarse que el signo positivo (+) de la fórmula en el apartado anterior, fue sustituido por un signo negativo (-).

Ejercicio 4
Un producto marcaba 800€, pero recibió un descuento de 15%. ¿Cuál es el nuevo precio del producto?
Solución 4
El precio final de acuerdo a la fórmula es:
f = 800€ * (1 – 15 / 100) = 800€ * ( 1 – 0,15 ) = 800€ * ( 0,85 ) = 680€
El precio final con el descuento del 15% es de 680€, lo que representa un ahorro de 120€.
Porcentajes sucesivos
Aparece cuando alguna cantidad sufre una variación porcentual y seguidamente se aplica otra, también porcentual. Por ejemplo un producto que ha tenido dos descuentos porcentuales seguidos. Otro ejemplo es el de un empleado que tuvo dos aumentos salariales consecutivos.
– Aumentos porcentuales sucesivos
La base de solución de estos casos es la misma de los aumentos únicos, pero hay que tener en cuenta que el segundo aumento porcentual se efectúa sobre el valor final del primer aumento.
Suponga un producto que subió primero 10% y luego 5%. Es incorrecto decir que sufrió un aumento del 15%, en realidad fue más de este porcentaje.
Las fórmulas para el valor final se aplicarían así:
-Primero se calcula el valor final del primer aumento de n1%
f1 = i + i * n1 / 100
-Y luego, para hallar el valor final del segundo aumento de n2%, se toma como valor inicial el valor final de f1. Por lo tanto:
f2 = f1 + f1 * n2 /100
Ejercicio 5
Un libro costaba originalmente 55€, pero debido al éxito del mismo y a la alta demanda, sufrió dos aumentos consecutivos sobre el precio original. El primer aumento fue de 10% y el segundo de 20%. ¿Cuál es el precio final del libro?
Solución
-Primer aumento:
f1 = 55€ * ( 1 + 10 /100 ) = 55€ * 1,1 = 60,5€
-Segundo aumento
f2 = 60,5€ * ( 1 + 20 / 100) = 60,5€ * 1,2 = 72,6€
El precio final es de 72,6€.
Ejercicio 6
En referencia al ejercicio anterior. Los dos aumentos consecutivos: ¿a qué porcentaje de un aumento único sobre el precio original del libro corresponden?
Solución
Si llamamos n% al porcentaje de aumento único, la fórmula que relaciona este aumento porcentual único con el valor original y el valor final es:
f2 = i *( 1 + n / 100 )
Es decir:
72,6€ = 55€ + 55€ * (n / 100)
Despejando el porcentaje de aumento n% = (n /100), tenemos:
(n /100) = (72,6€ – 55€) / 55€ = 17.6€ / 55€ = 0,32
Por lo tanto:
n = 0,32 * 100 = 32
Al precio del libro se le aplicó un aumento porcentual total del 32%. Note que este aumento es superior a la suma de los dos aumentos porcentuales consecutivos.
– Descuentos porcentuales sucesivos
La idea es similar a la de los aumentos porcentuales sucesivos. El segundo descuento porcentual debe aplicarse siempre sobre el valor final del primer descuento, veamos un ejemplo:
Ejercicio 7
Un descuento del 10% seguido de un segundo descuento del 20% sobre un objeto, ¿a qué descuento porcentual único equivale?
Solución
-Primer descuento:
f1 = i – i * n1 / 100
-Segundo descuento
f2 = f1 – f1 * n2 / 100
Sustituyendo la primera ecuación en la segunda queda:
f2 = ( i – i * n1 / 100) – ( i – i * n1 / 100 ) * n2 /100
Desarrollando esta expresión, obtenemos:
f2 = i – i * n1 / 100 – i* n2 / 100 + i* (n1 / 100)(n2 / 100)
Sacando factor común i:
f2 = i * (1- n1% – n2% + n1%*n2%)
Por último se sustituyen los porcentajes indicados en la pregunta:
f2 = i * (1 – 10% – 20% + 10% * 20%) = i * (1 – 0,1 – 0,2 + 0,1 * 0,2)
f2 = i * (1 – 0,3 + 0,02) = i * ( 0,72 ) = i * ( 1 – 0.28 ) = i * ( 1 – 28 /100) = i* ( 1 – 28%)
Es decir que los descuentos sucesivos de 10% y 20%, corresponden a un descuento único del 28%.
Ejercicios avanzados
Intentemos estos ejercicios solamente cuando las ideas de los anteriores hayan quedado lo bastante claras.
Ejercicio 8
La base de un triángulo mide 10 cm y la altura 6 cm. Si la longitud de la base disminuye en 10% ¿En qué porcentaje debe aumentarse la altura para que el área del triángulo no cambie?
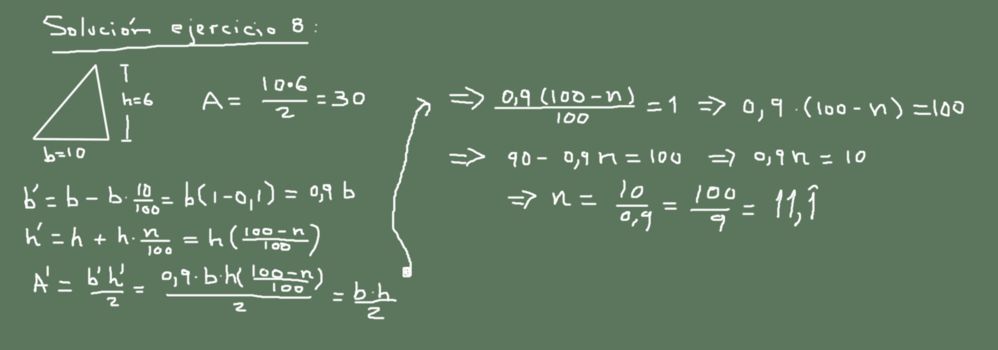
Solución 8
El área original del triángulo es:
A = (10cm * 6cm) / 2 = 30 cm2
Ahora bien, si la base disminuye en 10%, entonces su nuevo valor es:
Nueva base = 10 – (10/100) x 10 = 9 cm.
El nuevo valor de la altura será X, y el área original debe mantenerse inalterada, de modo que:
(9cm * X) /2 = 30 cm2
Entonces se despeja el valor de X como:
X= 60 cm2 / 9 cm = (20/3) cm = 6,666 cm
Lo que significa un aumento de 0,666 respecto al valor original. Veamos ahora qué porcentaje de este representa:
6,666 = 6 + (6 * n/100)
6,666 -6 = 6 * n/100
0.666 = 6 * n/100
n/100 = 0,111
n = 11,1
La respuesta es: la altura se debe incrementar un 11,1% para que el área del triángulo se mantenga igual.
Ejercicio 9
Si a un trabajador se le aumenta el sueldo en un 20%, pero luego el impuesto le descuenta el 5%, se pregunta: ¿cuál es el aumento real que percibe el trabajador?
Solución
Primero calculamos el aumento de n1%:
f1 = i + i * n1 / 100
Después aplicamos el descuento de n2%:
f2 = f1 – f1 * n2 / 100
Se sustituye la primera ecuación en la segunda:
f2 = i + i * n1 / 100 – (i + i * n1 / 100) * n2 / 100
Se desarrolla la expresión anterior:
f2 = i + i * n1 / 100 – i *n2 / 100 – i * (n1 / 100) * (n2 / 100)
Finalmente se saca i factor común y se sustituyen los valores de n1= 20 y n2 = 5 que aparecen en el enunciado:
f2 = i ( 1 + 0,2 – 0,05 – 0,2*0,05) = i* ( 1 + 7/50 ) = i*( 1 + 14/100) = i * ( 1 + 14%)
El trabajador recibió un aumento neto de 14%.
Ejercicio 10
Decidir qué es más conveniente entre estas dos opciones:
i) Adquirir camisetas con un descuento del 32 % cada una.
ii) Comprar 3 camisetas por el precio de 2.
Solución
Analizamos cada opción por separado y luego escogemos la más económica:
i) Sea X el precio actual de una camiseta, un 32 % de descuento representa un precio final de Xf:
Xf = X – (32/100)X= X – 0.32X = 0.68X
Por ejemplo, comprar 3 camisetas significa gastar 3 x 0.68 X = 2.04X
ii) Si X es el precio de una camiseta, por 3 camisetas simplemente se pagará 2X.
Supongamos que una camiseta vale 6 euros, con el descuento del 32 % valdría 4.08 euros. Comprar 1 camiseta no es una opción válida en la oferta de 3×2. Así que si solamente se desea comprar 1 camiseta, es preferible el descuento.
Pero si lo que se quiere es comprar por docenas, la oferta de 3×2 es apenas un poco más económica. Por ejemplo, 6 camisetas con el descuento saldrían por 24.48 euros, mientras que con la oferta de 3×2 costarían 24 euros
Referencias
- Aula Fácil. El Porcentaje. Recuperado de: aulafacil.com
- Baldor A. 2006. Aritmética teórico práctica. Ediciones Cultural.
- Educa Peques. Cómo aprender a calcular porcentajes. Recuperado de: educapeques.com
- Gutiérrez, G. Apuntes de Matemática Financiera. Recuperado de: csh.izt.uam.mx
- Smart ticks. Porcentaje: qué es y cómo se calcula. Recuperado de: smartick.es
