Igualdad matemática: propiedades, ejemplos y ejercicios resueltos

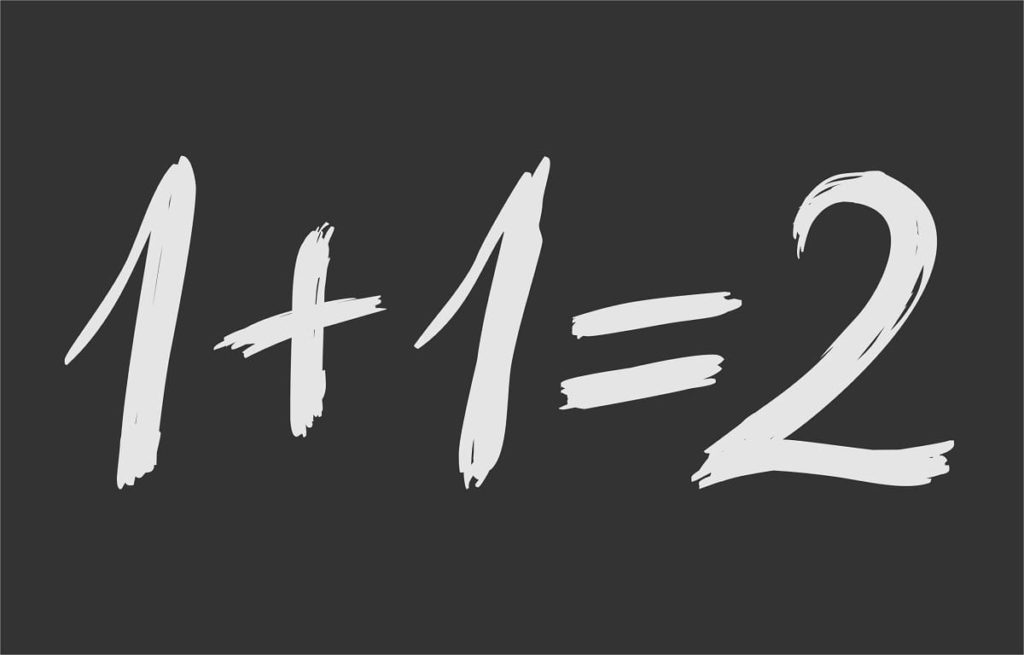
¿Qué es una igualdad matemática?

Una igualdad matemática asegura que dos expresiones, sean iguales o diferentes, son totalmente equivalentes. Estas expresiones pueden ser diversa naturaleza, por ejemplo  números, letras que simbolizan cantidades o magnitudes, combinaciones de números y letras, matrices y más.

El símbolo que se utiliza para denotar la igualdad en lenguaje matemático es el de dos líneas paralelas y horizontales, que en texto impreso es el conocido símbolo “=”. Por ejemplo, si se tienen tres manzanas, se puede escribir la siguiente igualdad:

Número de manzanas = 3

La frase “número de manzanas” es el miembro de la izquierda y el número 3 es el miembro a la derecha de la igualdad.

Como es posible escribir cantidades numéricas de diversas formas, la igualdad se emplea para denotarlas. Tomando un caso específico para ilustrar el punto, hay varias maneras de escribir el número 4, aparte de la más evidente que es 4 = 4, se pueden escribir las siguientes, a través de una igualdad matemática:

2 + 2 = 4
6 − 2 = 4
8  ÷ 2 = 4
2×2 = 4
2² = 4

Las igualdades mostradas hasta aquí son verdaderas, pero una igualdad puede no serlo, por ejemplo 10 + 5 = 20 es falsa, ya que 10 + 5 = 15.

Seguramente el lector conoce otras formas de escribir el número 4. Obsérvese que las expresiones a cada lado de la igualdad pueden ser números, palabras, letras que simbolizan cantidades u otros símbolos, por ejemplo:

x + 1 = 7
a²b − 1 = xy
f (x) = 2x²

Los matemáticos no siempre usaron el símbolo de igualdad, por eso los antiguos tratados de matemática era muy extensos.

Se le atribuye al matemático y médico Robert Recorde (1510-1558), nacido en Gales, la creación del símbolo de igualdad “=”, tan familiar para todos hoy en día. Recorde, al parecer cansado de escribir a cada rato la frase “igual que” en uno de sus tratados de Matemática, decidió abreviar escribiendo en su lugar las familiares rayas paralelas.

Propiedades de la igualdad matemática

Las siguientes propiedades permiten trabajar correctamente con las igualdades matemáticas. Son axiomáticas, por lo que no requieren demostración:

1.- Propiedad reflexiva

Esta propiedad establece que cualquier cantidad es igual a sí misma. En particular, como cualquier número es igual a sí mismo, se pueden escribir igualdades como:

5 = 5

36.35 = 36.35

Si una cantidad es literal, o es combinación de letras y números, también es igual a sí misma:

3x = 3x

a²bc^-1 = a²bc^-1

2.- Propiedad de simetría

Las cantidades o miembros a ambos lados de la igualdad se pueden intercambiar sin que se pierda validez. Es decir, si lo que se encuentra a la izquierda del símbolo “=” se escribe a su derecha, y lo que está a su derecha se coloca a la izquierda, se trata de la misma igualdad.

Por ejemplo, la expresión  5 + 2 = 7 es equivalente a esta otra: 7 = 5 + 2. De la misma manera:

12 + 8 = 20 ;  20 = 12 + 8

x + 1 = 3 ; 3 = x + 1

x – z = y ; y = x – z

3.- Propiedad transitiva

Esta propiedad se refiere a la equivalencia de igualdades. Si dos igualdades tienen un miembro común, entonces también son iguales entre sí, ya que en general:

Si “x = y” y “y = z” entonces x = z

Para ilustrar esta propiedad considérense estas dos igualdades numéricas: 2 + 2 = 4 y 6 − 2 = 4. Ya que ambas son iguales a 4 (tienen un miembro común), entonces se puede escribir lo siguiente, sin perder validez alguna:

2 + 2 = 6 − 2

Otro ejemplo, esta vez con letras:

Si x + 1 = 5

Y

a – b = 5

Entonces:

x+1 = a – b

4.- Propiedad de cancelación

Una igualdad no se altera si en ambos miembros hay una misma cantidad que esté sumando (o restando) y se decide eliminar o cancelar a esta. Esta es la propiedad de cancelación de la suma.

Tómese como ejemplo la siguiente igualdad numérica en la que el 10 aparece tanto en el miembro de la derecha como en el de la izquierda:

2 + 2 + 10 = 6 − 2 + 10

El número 10  se puede cancelar sin que la igualdad pierda su validez, quedando otra igualdad más corta y equivalente a la anterior:

2 + 2 = 6 − 2

En la igualdad (10 ÷ 2) − 3 = 5 − 3 el número entero − 3 pertenece a ambos miembros de la igualdad y aparece como sumando, por lo tanto se puede cancelar, obteniendo:

10 ÷ 2 = 5

Igualmente ocurre con cantidades literales, por ejemplo:

Si x + 2y + z = −a + b + z

Entonces la “z” se puede cancelar, ya que se encuentra a ambos lados de la igualdad como sumando (y con el mismo signo).

Al hacerlo resulta:

x + 2y = −a + b

Asimismo se puede definir la propiedad de cancelación de la multiplicación. Si una misma cantidad c multiplica a ambos miembros de una igualdad, esta cantidad se puede cancelar, por ejemplo:

cx = cy

Entonces c se puede cancelar para obtener simplemente:

x = y

5.- Propiedad de uniformidad

Una igualdad permanece invariable al sumar, restar, multiplicar o dividir por la misma cantidad a ambos lados de la misma.

Por ejemplo, se tiene que 8 + 5 = 13, si se multiplican ambos miembros por determinado número arbitrario c = 2, la igualdad se mantiene:

(8+5) × 2  = 13× 2

13 × 2 = 26

Clases de igualdades matemáticas

Hay diversos tipos de igualdades matemáticas, por lo que se clasifican para su mejor comprensión en:

–Identidades, son igualdades en las que ambos miembros son idénticos:

2 = 2
x = x
2x = x + x

Y así por el estilo.

–Ecuaciones, se trata de igualdades en las que aparece una o más incógnitas, y son ciertas para determinados valores, es decir, la igualdad no se cumple para cualquier valor arbitrario, por eso también se las conoce como igualdades condicionales. Ejemplos:

x + 1 = 5

x³ = 27

a + b = 40

–Equivalencias, en ellas el miembro de la izquierda equivale al de la derecha, aunque no sean iguales, por ejemplo en:  2³ = 8.

–Fórmulas, se trata de una igualdad que se cumple siempre para los valores de la variable independiente, como en la conocida fórmula para la distancia d en función del tiempo t de un móvil con movimiento rectilíneo uniforme: d = v ∙ t

Ejercicios resueltos

Ejercicio 1

Escribir el número 10 mediante cuatro igualdades distintas y equivalentes.

Solución

Todas estas igualdades expresan al número 10, pero de distintas maneras:

5×2 = 10

11–1 = 10

10¹=10

20÷2 =10

Ejercicio 2

¿Cuál es el valor de x que satisface la igualdad x + 1 = 3?

Solución

Esta igualdad es una ecuación, ya que el valor de x se desconoce. Haciendo uso de la propiedad 5, si a la expresión x + 1 = 3 se le suma (−1) a ambos lados del símbolo “=”, la igualdad se mantiene:

x + 1 + (−1) = 3+(−1)

Cuando se suma (−1) al miembro de la izquierda y se resuelve la operación, la “x” queda sola en el lado izquierdo de la igualdad, a este procedimiento se le denomina despeje:

x + 1 − 1 = 3−1

x = 2

Por lo tanto, el valor que satisface esta igualdad es x = 2.

Ejercicio 3

Si un móvil con movimiento rectilíneo uniforme tiene una rapidez de 2.5 m/s, ¿Cuál es la distancia que recorre al cabo de 3 segundos?

Solución

Se emplea la fórmula vista en el apartado anterior, d = v ∙ t, en la cual se sustituye el valor de v:

d = 2.5 ∙ t

La expresión se convierte en una igualdad cuando t = 3 segundos y se resuelve la operación:

d = 2.5 ∙ 3 m = 7.5 m

Que da como resultado la igualdad:

d = 7.5 m

Referencias

1. Barnett, R. 2000. Pre-cálculo. 4ta. Edición. McGraw Hill.
2. Larson, R. 2012. Pre-cálculo. 8va. Edición. Cengage Learning.
3. Pérez, V. Propiedades de la igualdad algebraica. Recuperado de: matematica.laguia2000.com.
4. Propiedades de la igualdad. Recuperado de: pps.k12.or.us.
5. Stewart, J. 2007. Pre-cálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.