Espacio vectorial: base y dimensión, axiomas, propiedades
Un espacio vectorial es un conjunto no vacío V={u, v, w, ……}, cuyos elementos son vectores. Con ellos se realizan algunas operaciones importantes, entre las cuales destacan las siguientes:
– Suma entre dos vectores u + v que da como resultado z, el cual pertenece al conjunto V.
– Multiplicación de un número real α por un vector v: α v que da otro vector y que pertenece a V.

Para denotar un vector usamos negrita (v es un vector), y para los escalares o números letras griegas (α es un número).
Índice del artículo
- 1 Axiomas y propiedades
- 2 Ejemplos de espacios vectoriales
- 3 Base y dimensión de un espacio vectorial
- 4 Ejercicios resueltos
- 5 Referencias
Para que se de un espacio vectorial, deben cumplirse los siguientes ocho axiomas:
1-Conmutabilidad: u +v = v +u
2-Transitividad: (u + v) + w = u + ( v + w)
3-Existencia del vector nulo 0 tal que 0 + v = v
4-Existencia del opuesto: el opuesto de v es (-v) , ya que v + (-v) = 0
5-Distributividad del producto respecto a la suma vectorial: α ( u + v ) = αu +αv
6-Distributividad del producto respecto a la suma escalar: (α + β)v = αv +βv
7-Asociatividad del producto de escalares: α (β v) = (α β)v
8-El número 1 es el elemento neutro ya que: 1v = v
Los vectores en el plano ( R² ) son un ejemplo de espacio vectorial. Un vector en el plano es un objeto geométrico que tiene magnitud y dirección. Se representa mediante un segmento orientado que pertenece a dicho plano y con un tamaño proporcional a su magnitud.
Se puede definir la suma de dos vectores en el plano como la operación geométrica de traslación del segundo vector a continuación del primero. El resultado de la suma es el segmento orientado que parte del origen del primero y llega a la punta del segundo.
En la figura se puede notar que la suma en R² es conmutativa.
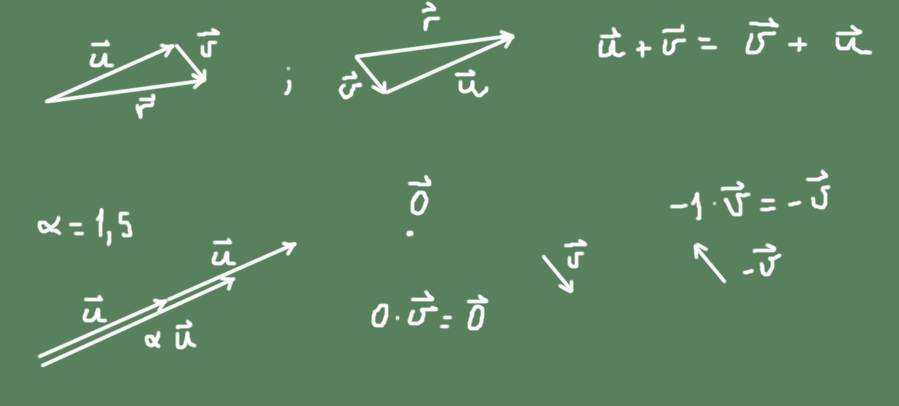
También se define el producto de un número α por un vector. Si el número es positivo, se mantiene la dirección del vector original y el tamaño es α veces el vector original. Si el número es negativo, la dirección es la opuesta, y el tamaño del vector resultante es el valor absoluto del número.
El vector opuesto a un vector cualquier v es –v =(-1) v.
El vector nulo es un punto en el plano R² , y el número cero por un vector da como resultado el vector nulo.
Todo lo dicho se ilustra en la figura 2.
El conjunto P de todos los polinomios de grado menor o igual a dos, incluyendo el grado cero, forman un conjunto que cumple todos los axiomas de un espacio vectorial.
Sea el polinomio P(x)= a x² + b x + c y Q(x)= d x² + e x + f
La suma de dos polinomios se define: P(x) + Q(x) = (a+d) x² + (b+e) x + (c+f)
La suma de polinomios perteneciente al conjunto P es conmutativa y transitiva.
El polinomio nulo perteneciente al conjunto P es aquel que tiene todos sus coeficientes igual a cero:
0(x) = 0 x² + 0 x + 0
Se define la suma de un escalar α por un polinomio como: α P(x) = α∙a x² + α∙b x + α∙c
El polinomio opuesto de P(x) es -P(x) = (-1) P(x).
De todo lo anterior se deduce que el conjunto P de todos los polinomios de grado menor o igual a dos, es un espacio vectorial.
El conjunto M de todas las matrices de m filas x n columnas cuyos elementos sean números reales forman un espacio vectorial real, respecto a las operaciones de suma de matrices y producto de un número por una matriz.
El conjunto F de funciones continuas de variable real, forman un espacio vectorial, ya que se puede definir la suma de dos funciones, la multiplicación de un escalar por una función, la función nula y la función simétrica. Además cumplen los axiomas que caracterizan a un espacio vectorial.
Se define como base de un espacio vectorial a un conjunto de vectores linealmente independientes tales que a partir de una combinación lineal de ellos se puede generar cualquier vector de ese espacio vectorial.
Combinar linealmente dos o más vectores consiste en multiplicar los vectores por algún escalar y luego sumarlos vectorialmente.
Por ejemplo, en el espacio vectorial de vectores en tres dimensiones conformado por R³ se usa la base canónica definida por los vectores unitarios ( de magnitud 1) i, j, k.
Donde i = ( 1, 0, 0 ); j = ( 0, 1, 0 ); k = (0, 0, 1). Estos son los vectores cartesianos o canónicos.
Un vector cualquiera V perteneciente a R³ se escribe como V = a i + b j + c k, que es una combinación lineal de los vectores base i, j, k. A los escalares o números a, b, c se les conoce como las componentes cartesianas de V.
Se dice también que los vectores base de un espacio vectorial forman un conjunto generador del espacio vectorial.
La dimensión de un espacio vectorial es el número cardinal de una base vectorial para dicho espacio; es decir, el número de vectores que conforman dicha base.
Este cardinal es el máximo número de vectores linealmente independientes de ese espacio vectorial, y a la vez el mínimo número de vectores que forman un conjunto generador de dicho espacio.
Las bases de un espacio vectorial no son únicas, pero todas las bases de un mismo espacio vectorial tienen la misma dimensión.
Un subespacio vectorial S de un espacio vectorial V es un subconjunto de V en el que se definen las mismas operaciones que en V y cumple todos los axiomas de espacio vectorial. Por lo tanto, el subespacio S también será un espacio vectorial.
Ejemplo de subespacio vectorial son los vectores que pertenecen al plano XY. Este subespacio es un subconjunto de un espacio vectorial de dimensionalidad mayor que el conjunto de vectores pertenecientes al espacio tridimensional XYZ.
Otro ejemplo de subespacio vectorial S1 del espacio vectorial S formado por todas las matrices 2×2 con elementos reales es el definido a continuación:
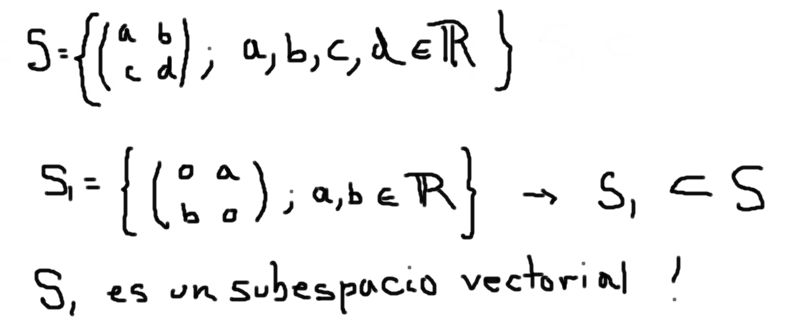
En cambio S2 definido a continuación, aunque es un subconjunto de S, no forma subespacio vectorial:

Sean los vectores V1=(1, 1, 0); V2=(0, 2, 1) y V3=(0, 0, 3) en R³.
a) Demostrar que son linealmente independientes.
b) Demostrar que forman una base en R³, ya que cualquier terna (x,y,z) puede escribirse como combinación lineal de V1, V2, V3.
c) Encuentre las componentes de la terna V = (-3,5,4) en la base V1, V2, V3.
Solución
El criterio para demostrar independencia lineal consiste en establecer el siguiente conjunto de ecuaciones en α, β y γ
α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)
En caso de que la única solución a este sistema sea α=β=γ=0 entonces los vectores son linealmente independientes, en caso contrario no lo son.
Para conseguir los valores de α, β y γ planteamos el siguiente sistema de ecuaciones:
α∙1 + β∙0 + γ∙0 =0
α∙1 + β∙2 + γ∙0 =0
α∙0 + β∙1 + γ∙3 =0
La primera conduce a α=0, la segunda α=-2∙β pero como α=0 entonces β=0. La tercera ecuación implica que γ=(-1/3)β, pero como β=0 entonces γ=0.
Respuesta a
Se concluye que se trata de un conjunto de vectores linealmente independientes en R³ .
Respuesta b
Ahora pasemos a escribir la terna (x,y,z) como combinación lineal de V1, V2, V3.
(x,y,z)=α V1 + β V2 + γ V3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)
α∙1 + β∙0 + γ∙0 =x
α∙1 + β∙2 + γ∙0 =y
α∙0 + β∙1 + γ∙3 =z
De donde se tiene:
α=x
α + 2 β = y
β + 3 γ = z
La primera nos indica α=x, la segunda β = (y-x)/2 y la tercera γ = (z- y/2 +x/2)/3. De este modo hemos encontrado los generadores de α, β y γ de cualquier terna de R³
Respuesta c
Pasemos a encontrar las componentes de la terna V = (-3,5,4) en la base V1, V2, V3.
Sustituimos los valores correspondientes en las expresiones encontradas anteriormente para los generadores.
En este caso tenemos: α=-3; β = (5-(-3))/2=4; γ = (4- 5/2 +(-3)/2)/3=0
Es decir, que:
(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)
Por último:
V = -3 V1 + 4 V2 + 0 V3
Concluimos que V1, V2, V3 forman una base en el espacio vectorial R³ de dimensión 3.
Expresar el polinomio P(t) = t² + 4t -3 como combinación lineal de P1(t) = t² -2t + 5, P2(t) = 2t² -3t y P3(t) = t+3.
Solución
P(t) = x P1(t) + y P2(t) + z P3(t)
donde los números x, y, z han de determinarse.
Al multiplicar y agrupar términos con el mismo grado en t se obtiene:
t² + 4 t -3 = (x + 2y) t² + (-2x -3y +z) t + (5x + 3z)
Lo que nos conduce al siguiente sistema de ecuaciones:
x + 2y = 1
-2x -3y + z = 4
5x + 3z = -3
Las soluciones de este sistema de ecuaciones son:
x= -3, y= 2, z= 4.
Es decir, que:
P(t) = -3 P1(t) + 2 P2(t) + 4 P3(t)
Demuestre que los vectores v1=(1, 0, -1, 2); v2=(1, 1, 0, 1) y v3=(2, 1, -1, 1) de R⁴ son linealmente independientes.
Solución
Combinamos linealmente los tres vectores v1, v2, v3 y exigimos que la combinación sume el elemento nulo de R⁴
a v1 + b v2 + c v3 = 0
Es decir,
a (1, 0, -1, 2) + b (1, 1, 0, 1) + c (2, 1, -1, 1) = (0, 0, 0, 0)
Esto nos conduce al siguiente sistema de ecuaciones:
a + b + 2 c = 0
b + c = 0
-a – c = 0
2 a + b + c = 0
Restando la primera y la cuarta nos queda: -a + c = 0 lo que implica a =c.
Pero si nos fijamos en la tercera ecuación, tenemos que a = -c. La única forma de que se cumpla a=c=(-c) es que c sea 0 y por tanto a también será 0.
a = c =0
Si sustituimos este resultado en la primera ecuación entonces concluimos que b=0.
Finalmente a=b=c=0, de modo que puede concluirse que los vectores v1, v2 y v3 son linealmente independientes.
- Lipschutz, S. 1993. Álgebra lineal. Segunda edición. McGraw – Hill. 167 – 198.
