Amplitud de onda: características, fórmulas y ejercicio
La amplitud de onda es el desplazamiento máximo que experimenta un punto de una onda respecto a la posición de equilibrio. Las ondas se manifiestan por doquier y de muchas formas en el mundo que nos rodea: en el océano, en el sonido y en la cuerda de un instrumento que lo produce, en la luz, sobre la superficie terrestre y mucho más.
Una forma de producir ondas y estudiar su comportamiento es observando la vibración de una cuerda que tiene un extremo fijo. Al producir una perturbación en el otro extremo, cada partícula de la cuerda oscila y con ello la energía de la perturbación se transmite en forma de una sucesión de pulsos a todo lo largo.

A medida que se va propagando la energía, la cuerda que se supone perfectamente elástica, adopta la típica forma sinusoidal con crestas y valles que se muestra en la figura que aparece más abajo en la sección siguiente.
Índice del artículo
- 1 Características y significado de la amplitud de onda
- 2 La descripción matemática de una onda
- 3 Descripción de la onda en el tiempo: parámetros característicos
- 4 Ejercicio resuelto
La amplitud A es la distancia entre la cresta y el eje de referencia o nivel 0. Si se prefiere, entre un valle y el eje de referencia. Si la perturbación en la cuerda es leve, la amplitud A es pequeña. Si por el contrario la perturbación es intensa, la amplitud será mayor.
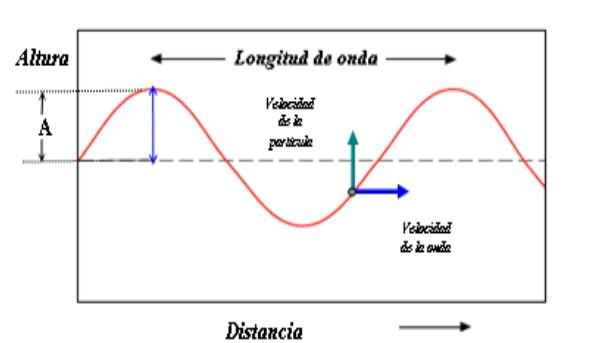
El valor de la amplitud también es una medida de la energía que porta la onda. Es intuitivo que una gran amplitud esté asociada a mayores energías.
De hecho la energía es proporcional al cuadrado de la amplitud, que expresado matemáticamente es:
I ∝A2
Donde I es la intensidad de la onda, a su vez relacionada a la energía.
El tipo de onda producida en la cuerda del ejemplo, pertenece a la categoría de las ondas mecánicas. Una característica importante es que cada partícula en la cuerda se mantiene siempre muy cerca de su posición de equilibrio.
Las partículas no se mueven o se desplazan a través de la cuerda. Ellas oscilan hacia arriba y hacia abajo. Esto se indica en el esquema de arriba con la flecha verde, sin embargo la onda junto con su energía, viaja de izquierda a derecha (flecha azul).
Las ondas que se propagan en el agua proveen la evidencia necesaria para convencerse de esto. Observando el movimiento de una hoja que ha caído en un estanque se aprecia que ella simplemente oscila acompañando el movimiento del agua. No llega muy lejos, a menos claro está, de que existan otras fuerzas que le proporcionen otros movimientos.
El modelo de onda mostrado en la figura consiste en un patrón repetitivo en el cual la distancia entre dos crestas es la longitud de onda λ. Si se quiere, la longitud de onda también separa dos puntos idénticos de la onda, aún cuando no estén sobre la cresta.
Naturalmente, a la onda se la puede describir mediante una función matemática. Las funciones periódicas como seno y coseno son las ideales para la tarea, ya sea que se quiera representar la onda tanto en el espacio como en el tiempo.
Si al eje vertical en la figura lo llamamos “y” y al eje horizontal lo llamamos “t”, entonces el comportamiento de la onda en el tiempo se expresa mediante:
y = A cos (ωt + δ)
Para este movimiento ideal, cada partícula de la cuerda oscila con movimiento armónico simple, el cual se origina gracias a una fuerza que es directamente proporcional al desplazamiento realizado por la partícula.
En la ecuación propuesta, A, ω y δ son parámetros que describen el movimiento, siendo A la amplitud definida anteriormente como el máximo desplazamiento experimentado por la partícula respecto al eje de referencia.
Al argumento del coseno se le denomina fase del movimiento y δ es la constante de fase, que es la fase cuando t = 0. Tanto la función coseno como la función seno son apropiadas para describir una onda, ya que solamente difieren entre sí π/2.
Por lo general es posible elegir t= 0 con δ = 0 para simplificar la expresión, obteniéndose:
y = A cos (ωt)
Al ser repetitivo el movimiento tanto en el espacio como en el tiempo, existe un tiempo característico que es el período T, definido como el tiempo que tarda la partícula en ejecutar una oscilación completa.
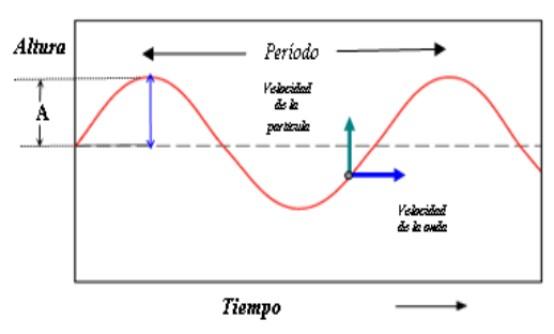
Ahora bien, tanto el seno como el coseno repiten su valor cuando la fase se incrementa en el valor 2π, de manera que:
ωT = 2π → ω=2π /T
A ω se le denomina frecuencia angular del movimiento y tiene dimensiones del inverso del tiempo, siendo sus unidades en el sistema internacional radián / segundo o segundo-1.
Finalmente se puede definir la frecuencia del movimiento f, como la inversa o recíproco del período. Representa en el número de crestas por unidad de tiempo, en cuyo caso:
f = 1/T
ω = 2πf
Tanto f como ω tienen las mismas dimensiones y unidades. Además del segundo-1, el cual se denomina Hertz o hertzio, es común oír hablar de revoluciones por segundo o revoluciones por minuto.
La velocidad de la onda v, la cual es preciso recalcar que no es la misma que la experimentada por las partículas, se puede calcular fácilmente si se conocen la longitud de onda λ y la frecuencia f:
v = λf
Si la oscilación experimentada por las partículas es del tipo armónico simple, la frecuencia angular y la frecuencia dependen únicamente de la naturaleza de las partículas oscilantes y de las características del sistema. La amplitud de la onda no afecta estos parámetros.
Por ejemplo al tocar una nota musical en una guitarra, la nota siempre tendrá el mismo tono aunque se toque con mayor o menor intensidad, de esta manera un do sonará siempre como un do, pese a que se escuche más fuerte o más suave en una composición, ya sea en un piano o en una guitarra.
En la naturaleza, las ondas que se transportan en un medio material en todas las direcciones se atenúan a causa de que la energía se disipa. Por ese motivo la amplitud decrece con el inverso de la distancia r a la fuente, siendo posible afirmar que:
A∝1/r
La figura muestra la función y (t) para dos ondas, donde y está en metros y t en segundos. Para cada una encuentre:
a) Amplitud
b) Período
c) Frecuencia
d) La ecuación de cada onda en términos de senos o cosenos.
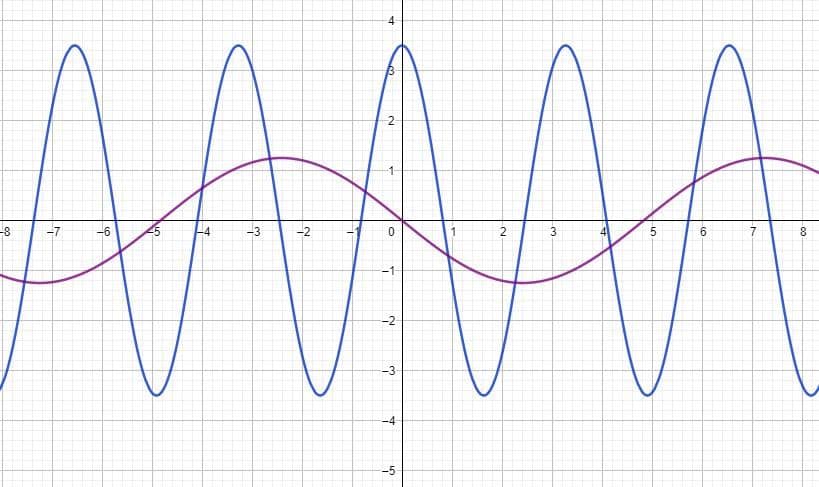
a) Se mide directamente del gráfico, con ayuda de la cuadrícula: onda azul: A = 3.5 m; onda fucsia: A = 1.25 m
b) También se lee del gráfico, determinando la separación entre dos picos o valles, consecutivos: onda azul: T = 3.3 segundos; onda fucsia T = 9.7 segundos
c) Se calcula recordando que la frecuencia es el recíproco del período: onda azul: f = 0.302 Hz ; onda fucsia: f = 0.103 Hz.
d) Onda azul: y (t) = 3.5 cos (ωt) = 3.5 cos (2πf.t) = 3.5 cos (1.9t) m; Onda fucsia: y (t) =1.25 sen (0.65t) = 1.25 cos (0.65t+1.57)
Obsérvese que la onda fucsia está desfasada π/2 respecto a la azul, siendo posible representarla con una función seno. O bien coseno desplazado π/2.
