Programación no lineal: métodos y ejercicios
La programación no lineal es el proceso de optimizar una función que depende de varias variables independientes, las cuales a su vez están sometidas a restricciones.
Si una o más de las restricciones, o si la función a maximizar o minimizar (llamada función objetivo), no está expresada como una combinación lineal de las variables, entonces se tiene un problema de programación no lineal.

Y por tanto no pueden emplearse los procedimientos y métodos de la programación lineal.
Por ejemplo, no puede usarse el conocido método Simplex, el cual solo se aplica cuando la función objetivo y las restricciones son todas combinación lineal de las variables del problema.
Índice del artículo
Para los problemas de programación no-lineal los principales métodos a ser usados son:
1.- Métodos gráficos.
2.- Multiplicadores de Lagrange para explorar la frontera de la región de solución.
3.- Cálculo de la gradiente para explorar extremos de la función objetivo.
4.- El método de los pasos descendentes, para encontrar los puntos de gradiente nulo.
5.- Método modificado de los multiplicadores de Lagrange (con la condición de Karush-Kuhn-Tucker).
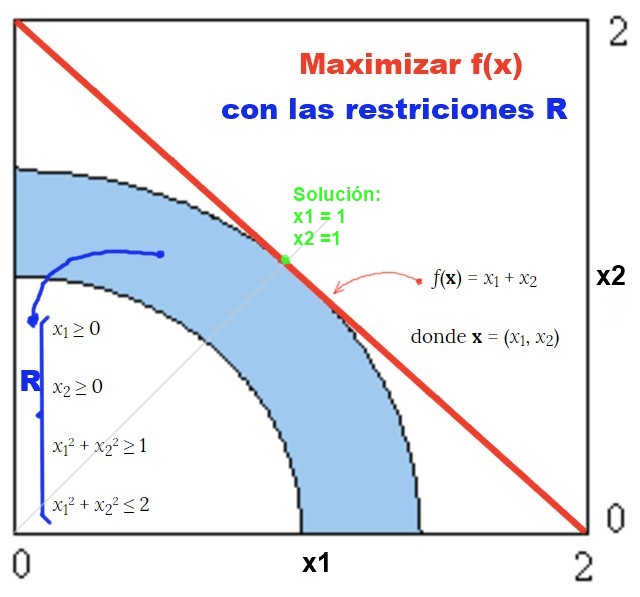
Un ejemplo de solución con el método gráfico es el que puede apreciarse en la figura 2:
La ganancia G de cierta empresa depende del monto vendido del producto X y el monto vendido del producto Y, además la ganancia se determina por la siguiente fórmula:
G = 2(X – 2)2 + 3(Y – 3)2
Se sabe que los montos X e Y tienen las siguientes restricciones:
X≥0 ; Y≥0 y X + Y ≤ 7
Determine los valores de X e Y que producen la máxima ganancia.

Solución
En este problema la función objetivo es no lineal, mientras que las desigualdades que definen las restricciones sí lo son. Se trata de un problema de programación no lineal.
Para la solución de este problema se optará por el método gráfico.
En primer lugar se determinará la región de solución, la cual está dada por las restricciones.
Como X≥0 ; Y≥0, la solución se tiene que buscar en el primer cuadrante del plano XY, pero como adicionalmente debe cumplirse que X + Y ≤ 7, la solución está en el semiplano inferior de la recta X + Y = 7.
La región de solución es la intersección del primer cuadrante con el semiplano inferior de la recta, lo que da lugar a una región triangular donde se encuentra la solución. Es la misma que se indica en la figura 1.
Por otra parte, la ganancia G también puede representarse en el plano cartesiano, ya que su ecuación es la de una elipse con centro (2,3).
La elipse se muestra en la figura 1 para varios valores de G. A mayor valor de G, mayor ganancia.
Hay soluciones que pertenecen a la región, pero no dan el máximo valor G, mientras que otras, como G= 92.4, están fuera de la zona verde, es decir la zona de solución.
Entonces, el máximo valor de G, tal que X e Y pertenezca a la región de solución corresponde a:
G = 77 (ganancia máxima), la cual se da para X=7 e Y=0.
Curiosamente, la máxima ganancia ocurre cuando el monto de ventas del producto Y es nulo, mientras que el monto del producto X alcanza su mayor valor posible.
Encontrar la solución (x, y) que hace que la función f(x, y) = x2 + 2y2 sea máxima en la región g(x,y) = x2 + y2 – 1 = 0.
Solución
Se trata claramente de un problema de programación no-lineal, ya que tanto la función objetivo f(x,y) como la restricción g(x,y) = 0, no son combinación lineal de las variables x e y.
Se usará el método de los multiplicadores de Lagrange, el cual requiere en primer lugar definir la función de Lagrange L(x, y, λ):
L(x, y, λ) = f(x,y) – λ g(x,y) = x2 + 2y2 – λ (x2 + y2 – 1)
Donde λ es un parámetro denominado multiplicador de Lagrange.
Para determinar los valores extremos de la función objetivo f, en la región de solución dada por la restricción g(x,y)=0, se siguen estos pasos:
-Hallar las derivadas parciales de la función de Lagrange L, respecto de x, y, λ.
-Igualar a cero cada derivada.
Aquí la secuencia de dichas operaciones:
- ∂L/∂x = 2x – 2λx = 0
- ∂L/∂y = 4y – 2λy = 0
- ∂L/∂λ = -(x2 + y2 – 1) = 0
Soluciones posibles del sistema
Una solución posible de este sistema es λ=1 para que se satisfaga la primera ecuación, en cuyo caso y=0 para que se cumpla la segunda.
Esta solución implica que x=1 o x=-1 para que se satisfaga la tercera ecuación. De esta forma se han obtenido dos soluciones S1 y S2:
S1: (x=1, y=0)
S2: (x=-1, y=0).
La otra alternativa es que λ=2 para que se satisfaga la segunda ecuación, independientemente del valor y.
En este caso, la única forma para que se satisfaga la primera ecuación es que x=0. Considerando la tercera ecuación, solo hay dos soluciones posibles, las cuales llamaremos S3 y S4:
S3: (x=0, y=1)
S4: (x=0, y=-1)
Para saber cuál o cuáles de estas soluciones maximizan la función objetivo, se procede a sustituir en f(x, y):
S1: f(1, 0) = 12 + 2.02 = 1
S2: f(-1, 0) = (-1)2 + 2.02 = 1
S3: f(0, 1) = 02 + 2.12 = 2
S4: f(0, -1) = 02 + 2 (-1)2 = 2
Concluimos que las soluciones que maximizan a f, cuando x e y pertenecen a la circunferencia g(x, y) = 0 son S3 y S4.
Los pares de valores (x=0, y=1) y (x=0, y=-1) maximizan f(x,y) en la región de solución g(x,y) = 0.
Encontrar soluciones (x, y) para que la función objetivo:
f(x, y) = x2 + 2 y2
Sea máxima en la región g(x,y) = x2 + y2 – 1 ≤ 0.
Solución
Este ejercicio es similar al ejercicio 2, pero la región de solución (o restricción) se extiende a la región interior de la circunferencia g(x,y)=0, es decir al círculo g(x,y) ≤ 0. Esto incluye a la circunferencia y su región interior.
La solución en la frontera ya fue determinada en el ejercicio 2, pero falta explorar la región interior.
Para ello debe calcularse la gradiente de la función f(x, y) e igualarla a cero, para buscar valores extremos en la región de solución. Esto es equivalente a calcular las derivadas parciales de f respecto de x e y respectivamente e igualar a cero:
∂f/∂x = 2 x = 0
∂f/∂y = 4 y = 0
Este sistema de ecuaciones tiene como única solución (x=0, y=0) que pertenece al círculo g(x,y) ≤ 0.
Sustituyendo este valor en la función f resulta:
f(0, 0) = 0
En conclusión, el valor máximo que toma la función en la región de solución es 2 y ocurre en la frontera de la región solución, para los valores (x=0, y=1) y (x=0, y=-1).
- Avriel, M. 2003. Nonlinear Programing. Dover Publishing.
- Bazaraa. 1979. Nonlinear Programing. John Wiley & Sons.
- Bertsekas, D. 1999. Nonlinear Programing: 2nd edition. Athena Scientific.
- Nocedal, J. 1999. Numerical Optimization. Springer-Verlag.
- Wikipedia. Programación no lineal. Recuperado de: es.wikipedia.com
