Probabilidad frecuencial: concepto, cómo se calcula y ejemplos
La probabilidad frecuencial es una sub-definición dentro del estudio de la probabilidad y sus fenómenos. Su método de estudio con respecto a los eventos y atributos, se basa en grandes cantidades de iteraciones, observando así la tendencia de cada uno a largo plazo o incluso a infinitas repeticiones.
Por ejemplo un sobre de gomitas contiene 5 gomas de cada color: azul, rojo, verde y amarillo. Se quiere determinar la probabilidad que cada color tiene de salir tras una selección aleatoria.

Es tedioso imaginar sacar una goma, registrarla, devolverla, sacar una goma y repetir lo mismo varios centenares o varios miles de veces. Incluso se puede querer observar el comportamiento tras varios millones de iteraciones.
Pero al contrario resulta interesante descubrir, que al cabo de pocas repeticiones la probabilidad esperada de 25% no se cumple a cabalidad, al menos no para todos los colores tras ocurrir 100 iteraciones.
Bajo el enfoque de la probabilidad frecuencial, la asignación de los valores será únicamente a través del estudio de muchas iteraciones. De esta manera el proceso debe realizarse y registrarse preferiblemente de manera computarizada o emulada.
Múltiples corrientes rechazan la probabilidad frecuencial, argumentando falta de empirismo y confiabilidad en los criterios de aleatoriedad.
Índice del artículo
- 1 ¿Cómo se calcula la probabilidad frecuencial?
- 2 Otros enfoques de la probabilidad
- 3 Historia
- 4 Ejemplo
Al programar el experimento en cualquier interfaz capaz de ofrecer una iteración netamente aleatoria, se puede comenzar a estudiar la probabilidad frecuencial del fenómeno mediante una tabla de valores.
Se aprecia el ejemplo anterior desde el enfoque frecuencial:
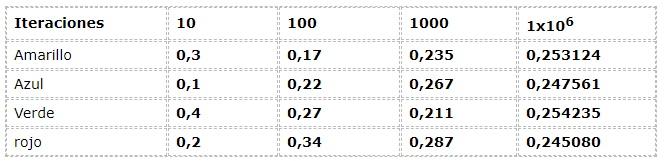
Los datos numéricos corresponden a la expresión:
N (a) = Número de ocurrencias/ Número de iteraciones
Donde N (a) representa la frecuencia relativa del suceso “a”
“a” pertenece al conjunto de resultados posibles o espacio muestral Ω
Ω : { rojo , verde , azul , amarillo }
Se aprecia una dispersión considerable en las primeras iteraciones, al observarse frecuencias con hasta 30% de diferencias entre sí, lo cual es un dato muy elevado para un experimento que teóricamente posee eventos con igual posibilidad (Equiprobable).
Pero a medida que crecen las iteraciones los valores parecen ajustarse cada vez más a los presentados por la corriente teórica y lógica.
Como un acuerdo inesperado entre los enfoques teórico y frecuencial surge la ley de los grandes números. Donde se establece que tras una considerable cantidad de iteraciones, los valores del experimento frecuencial se van aproximando a los valores teóricos.
En el ejemplo se puede notar como los valores se aproximan a 0,250 a medida que las iteraciones crecen. Este fenómeno es elemental en las conclusiones de muchos trabajos probabilísticos.

Existen otras 2 teorías o enfoques de la noción de probabilidad además de la probabilidad frecuencial.
Su enfoque está orientado a la lógica deductiva de los fenómenos. En el ejemplo anterior la probabilidad de obtener cada color es 25% de manera cerrada. Es decir que sus definiciones y axiomas no contemplan desfases fuera de su rango de datos probabilísticos.
Está basada en el conocimiento y creencias previas que cada individuo tiene sobre los fenómenos y atributos. Afirmaciones como “Siempre llueve en semana santa” obedecen a un patrón de sucesos similares que han ocurrido con anterioridad.
Los comienzos de su implementación datan del siglo XIX, cuando Venn la cito en varios de sus trabajos en Cambridge Inglaterra. Pero no fue sino hasta ya entrado el siglo XX que 2 matemáticos estadísticos desarrollaron y dieron forma a la probabilidad frecuencial.
Uno de ellos fue Hans Reichenbach, quien desarrolla su obra en publicaciones como “The Theory of Probability” publicada en 1949.
El otro fue Richard Von Mises, quien desarrolló más a fondo su obra mediante múltiples publicaciones y propuso considerar a la probabilidad como una ciencia matemática. Este concepto era nuevo en las matemáticas y marcaría el inicio de una era de crecimiento en el estudio de la probabilidad frecuencial.
En realidad este suceso marca la única diferencia con los aportes hechos por la generación de Venn, Cournot y Helm. Donde la probabilidad pasa a ser homóloga de ciencias como la geometría y la mecánica.
La teoría de las probabilidades trata con fenómenos masivos y eventos repetitivos. Problemas en los cuales o bien el mismo evento se repite una y otra vez, o un gran número de elementos uniformes están involucrados al mismo tiempo > Richard Von Mises
Se pueden clasificar tres tipos:
- Físicos: obedecen a patrones de la naturaleza más allá de una condición de aleatoriedad. Por ejemplo el comportamiento de las moléculas de un elemento en una muestra.
- Azar: su consideración fundamental es la aleatoriedad, como al lanzar un dado en repetidas veces.
- Estadística biológica: selecciones de sujetos de prueba según sus características y atributos.
En la teoría, el individuo que mide juega un papel en el dato probabilístico, debido a que son sus conocimientos y vivencias las que articulan este valor o predicción.
En la probabilidad frecuencial se considerarán a los eventos como colecciones a tratar, donde el individuo no juega ningún rol en la estimación.
En cada elemento ocurre un atributo, el cual será variable según la naturaleza de este. Por ejemplo en el tipo de fenómeno físico las moléculas de agua tendrán distintas velocidades.
En el lanzamiento de los dados conocemos el espacio muestral Ω que representa a los atributos del experimento.
Ω : { 1 , 2 , 3 , 4 , 5 , 6 }
Existen otros atributos como ser par ΩP o ser impar ΩI
Ωp : { 2 , 4 , 6 }
ΩI : { 1 , 3 , 5 }
Los cuales pueden definirse como atributos no elementales.
- Se quiere calcular la frecuencia de cada sumatoria posible en el lanzamiento de dos dados.
Para esto se programa un experimento donde dos fuentes de valores aleatorios entre [1 , 6] se sumen en cada iteración.
Los datos se registran en una tabla y se estudian las tendencias en los grandes números.
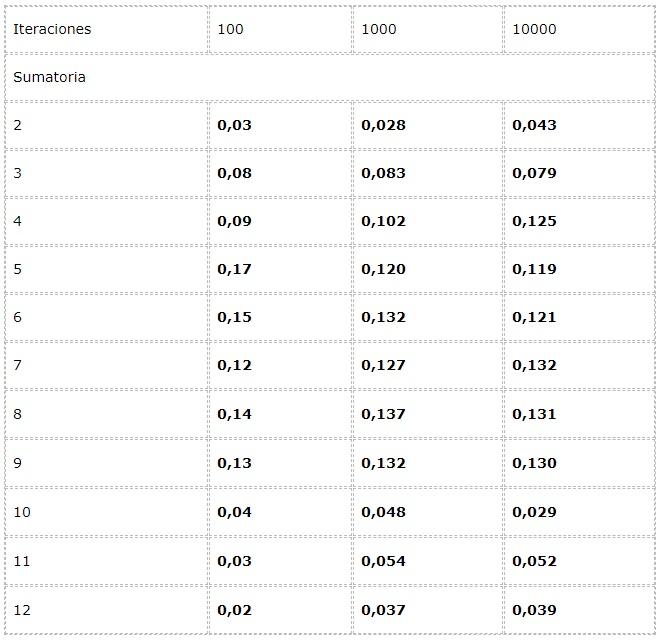
Se observa que los resultados pueden variar notablemente entre las iteraciones. Sin embargo la ley de los grandes números puede apreciarse en la aparente convergencia presentada en las dos últimas columnas.
- Statistics and the Evaluation of Evidence for Forensic Scientists. Second Edition. Colin G.G. Aitken. School of Mathematics. The University of Edinburgh, UK
- Mathematics for Computer Science. Eric Lehman. Google Inc.
F Thomson Leighton Department of Mathematics and the Computer Science and AI Laboratory, Massachussetts Institute of Technology; Akamai Technologies - The Arithmetic Teacher, Volumen 29. National Council of Teachers of Mathematics, 1981. Universidad de Michigan.
- Learning and teaching number theory: Research in cognition and instruction / edited by Stephen R. Campbell and Rina Zazkis. Ablex publishing 88 Post Road West, Westport CT 06881
- Bernoulli, J. (1987). Ars Conjectandi- 4ème partie. Rouen: IREM.
