Números perfectos: cómo identificarlos y ejemplos
Un número perfecto es un número natural tal que la suma de sus divisores es igual que el número. Obviamente no puede incluirse entre los divisores al propio número.
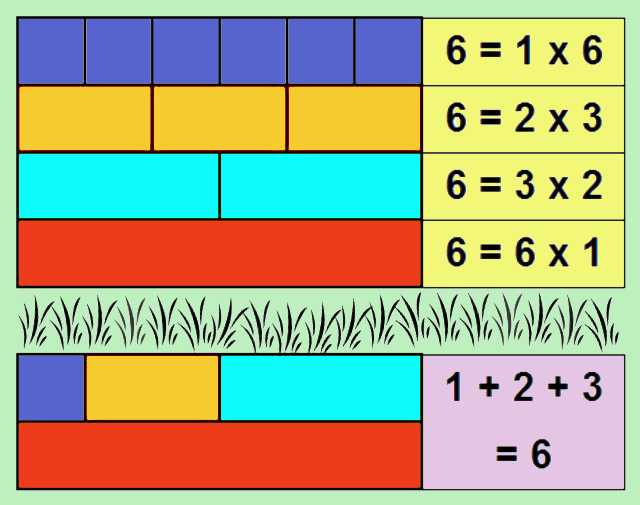
Uno de los ejemplos más simples de número perfecto es el 6, ya que sus divisores son: 1, 2 y 3. Si sumamos los divisores se obtiene: 1 + 2 + 3 = 6.
La suma de los divisores de un entero, sin incluir al propio número, se llama alícuota. Por tanto un número perfecto es igual a su alícuota.
Pero si en la suma de divisores de un número se incluye al propio número, entonces un número perfecto será aquel que la suma de todos sus divisores dividido entre 2 es igual al propio número.
Índice del artículo
- 1 Historia
- 2 Propiedades de los números perfectos
- 3 Ejemplos de números perfectos
- 4 Ejercicios
- 5 Referencias
Los matemáticos de la antigüedad, particularmente los griegos, daban gran importancia a los números perfectos y les atribuían cualidades divinas.
Por ejemplo, Philo de Alejandría, hacia el siglo I, afirmaba que 6 y 28 son números perfectos que coinciden con los seis días de la creación del mundo y los veintiocho días que tarda la Luna en dar una vuelta en torno a la Tierra.
Los números perfectos también están presentes en la naturaleza, por ejemplo en el polo norte de Saturno también aparece el número perfecto 6, un vórtice en forma de hexágono hallado por la sonda Cassini y que tiene intrigados a los científicos.
Los panales de las abejas tienen celdas en forma hexagonal, es decir con 6 lados. Está demostrado que el polígono con el número perfecto 6 es el que permite maximizar el número de celdas en la colmena de abejas, con el mínimo de cera para su elaboración.

La suma de todos los divisores de un número natural n se denota por σ(n). En un número perfecto se cumple que: σ(n) = 2n.
Euclides descubrió una fórmula y un criterio que permite encontrar los números perfectos. Dicha fórmula es:
2(n-1) (2n -1)
Sin embargo, el número generado por la fórmula será perfecto únicamente cuando el factor (2n -1) sea primo.
Veamos cómo se generan los primeros números perfectos:
Si n=2 entonces nos queda 21 (22 – 1) = 2 x 3 = 6 que ya vimos que es perfecto.
Cuando n=3 se tiene 22 (23 – 1) = 4 x 7 = 28 que también es perfecto tal como se verifica detalladamente en el ejemplo 1.
Veamos que ocurre con n=4. Al sustituir en la fórmula de Euclides nos queda:
23 (24 – 1) = 8 x 15 = 120
Puede verificarse que este número no es perfecto, como se muestra detalladamente en el ejemplo 3. Esto no contradice el criterio de Euclides, ya que 15 no es primo, requisito necesario para que el resultado sea un número perfecto.
Veamos ahora qué ocurre cuando n=5. Aplicando la fórmula tenemos:
24 (25 – 1) = 16 x 31 = 496
Como 31 es un número primo, entonces el número 496 tiene que ser perfecto, de acuerdo al criterio de Euclides. En el ejemplo 4 se muestra detalladamente que efectivamente lo es.
Los números primos que tienen la forma 2p – 1 se llaman primos de Mersenne, en honor al monje Marin Mersenne, que estudió los números primos y los números perfectos allá por el siglo XVII.
Posteriormente en el siglo XVIII Leonhard Euler demostró que todos número perfectos generados por la fórmula de Euclides son pares.
Hasta la fecha no se ha encontrado un perfecto que sea impar.
A la fecha actual se conocen 51 números perfectos, todos generados mediante la fórmula y el criterio de Euclides. Este número se obtuvo una vez que fue hallado el primo de Mersenne más grande, que es: (282589933 – 1).
El número perfecto #51 es (282589933)x(282589933 – 1) y tiene 49724095 digitos.
En teoría de números se dice que dos números son amigos cuando la suma de los divisores de uno, sin incluir al propio número, es igual al otro número y viceversa.
El lector puede verificar que la suma de los divisores de 220, sin incluir el 220 es 284. Por otra parte la suma de los divisores de 284, sin incluir al 284, es igual a 220. Por lo tanto la pareja de números 220 y 284 son amigos.
Desde este punto de vista, un número perfecto es amigo de sí mismo.
A continuación se listan los primeros ocho números perfectos:
6
28
496
8128
33550336
8589869056
137438691328
2305843008139952128
En los siguientes ejercicios será necesario calcular los divisores de un número, para luego realizar la suma de los mismos y verificar si el número se trata de un número perfecto o no.
Por lo tanto antes de abordar los ejercicios revisaremos el concepto y mostraremos cómo se calculan.
Para empezar, hay que recordar que los números pueden ser primos (cuando solo pueden dividirse en exacta consigo mismo y el 1) o compuestos (cuando pueden descomponerse como un producto de números primos).
Para un número compuesto N se tiene:
N = an . bm. cp … rk
Donde a, b, c … r son números primos y n, m, p… k son exponentes pertenecientes a los números naturales, que pueden valer desde 1 en adelante.
En términos de estos exponentes, hay una fórmula para conocer cuántos divisores tiene el número N, aunque no nos dice cuáles son estos. Sea C esta cantidad, entonces:
C = (n +1) (m+1) (p +1)… (k+1)
La descomposición del número N como un producto de números primos y el conocimiento de cuántos divisores tiene, tanto primos como no primos, nos ayudará a determinar cuáles son estos divisores.
Una vez que se tengan todos, excepto el último que no se requiere en la suma, se puede comprobar si se trata de un número perfecto o no.
Verificar que el número 28 es perfecto.
Solución
Lo primero será descomponer el número en sus factores primos.
28|2
14|2
07|7
01|1
Sus divisores son: 1, 2, 4, 7, 14 y 28. Si excluimos el 28 la suma de los divisores da:
1 + 2 + 4 + 7 + 14 = 3 + 4 + 7 + 14 = 7 + 7 + 14 = 14 + 14 = 28
Por lo tanto el 28 es un número perfecto.
Además la suma de todos sus divisores es 28 + 28 por lo que se cumple la regla σ(28) = 2 x 28.
Decidir si el número 38 es perfecto o no.
Solución
Se descompone el número en sus factores primos:
39|3
13|13
01|1
Los divisores de 39 sin incluir al propio número son: 1, 3 y 13. La suma 1 + 3 + 13 = 4 + 13 = 17 no es igual a 39, por lo tanto 39 es un número imperfecto o no-perfecto.
Averiguar si el número 120 es perfecto o imperfecto.
Solución
Se procede a descomponer el número en sus factores primos:
120|2
060|2
30|2
15|3
5|5
1|1
A partir de los factores primos se procede a encontrar los divisores:
{1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 y 120}
Si 120 fuese perfecto al sumar todos sus divisores debería obtenerse 2 x 120 = 240.
1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360
Este resultado claramente es diferente de 240, por lo que se concluye que el número 120 no es un número perfecto.
Verificar que el número 496, obtenido mediante el criterio de Euclides, es un número perfecto.
Solución
Se descompone el número 496 en sus factores primos:
496|2
248|2
124|2
062|2
031|31
001|1
Entonces sus divisores son:
{1, 2, 4, 8, 16, 31, 62, 124, 248, 496}
Ahora se suman todos ellos, excepto 496:
1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496
Confirmándose que, efectivamente se trata de un número perfecto.
- Baldor, A. 1986. Aritmética. Ediciones y Distribuciones Códice.
- Todo sobre números primos. Números amigos. Recuperado de: numerosprimos.org.
- Wolfram MathWorld. Euler’s Rule. Recuperado de: mathworld.wolfram.com.
- Wolfram MathWorld. Perfect number. Recuperado de: mathworld.wolfram.com.
- Wikipedia. Perfect numbers. Recuperado de: en.wikipedia.org.
- Wikipedia. Números amigos. Recuperado de: es.wikipedia.org.
