¿Cuánto vale X?
En álgebra la letra X denota con frecuencia a una cantidad desconocida, que se denomina “incógnita”, justamente porque no se conoce. Puede tomar cualquier valor, dependiendo de la naturaleza de la expresión algebraica que la contenga.
Pongamos un ejemplo. Se tiene la expresión algebraica:
x + 1
Se le pueden asignar valores arbitrarios a la X y efectuar la operación. Por ejemplo, haciendo x = 2, se tiene:
2 + 1 = 3
Y haciendo x = 5, el resultado es diferente:
5 + 1 = 6
¿Cuánto vale X en una ecuación?
Muchas veces la X forma parte de una ecuación, que consiste en dos expresiones algebraicas separadas por un signo de igualdad. Dicha igualdad se cumple solo para determinados valores de X.
Un ejemplo:
x – 2 = 14
Esta igualdad es cierta únicamente para un valor de X, el cual es:
x = 16
Esto se verifica fácilmente si se sustituye X = 16 en la ecuación x – 2 = 14:
16 – 2 = 14
¿Cómo saber cuánto vale X?
El procedimiento para saber cuánto vale X depende del tipo de ecuación.
Las más sencillas son las ecuaciones de primer grado con una sola incógnita, que se llaman así porque el exponente de la X es igual a 1.
La ecuación del ejemplo anterior: x – 2 = 14, es una ecuación de primer grado cuya incógnita es X.
Fue muy fácil de resolver, puesto que solo había que encontrar un número al que se le restara 2 para obtener 14. Este número es 16.
No todas las ecuaciones tienen solución, y algunas tienen más de una.
Pasos para resolver una ecuación de primer grado
Supongamos que se tiene la ecuación:
5x – 1 = 2x –10
En este caso es fácil saber cuánto vale X para que se cumpla la igualdad.
Existen unos pasos que, al seguirlos cuidadosamente, permitirán calcular el valor de X:
- Trasponer los términos semejantes, que consiste en poner todos los términos semejantes a un mismo lado de la igualdad.
- Reducir los términos semejantes, lo cual quiere decir que se debe dejar un solo término a cada lado de la igualdad.
- Aislar la X y hallar su valor.
Sigamos los pasos mencionados:
1.- Trasponer:
5x – 2x = –10 + 1
En la ecuación de primer grado hay términos que contienen X y normalmente hay términos independientes, es decir, números. Trasponer los términos semejantes en este caso, significa dejar todos los términos que contienen X a un lado de la igualdad.
Casi siempre es el lado izquierdo, pero no hay problema si se elige el lado derecho siempre y cuando los signos se coloque adecuadamente. Obsérvese que para hacer esta operación, el término traspuesto cambia de signo.
2.- Reducir:
5x – 2x = –10 + 1
3x = –9
Reducir términos semejantes significa combinarlos todos para obtener uno solo.
3.- Aislar:
x = –9/3
x = –3
Aislar significa dejar sola la X y así saber su valor.
Ejemplo resuelto
¿Cuánto vale X en el siguiente triángulo, si se sabe que el perímetro es igual a 12 cm?
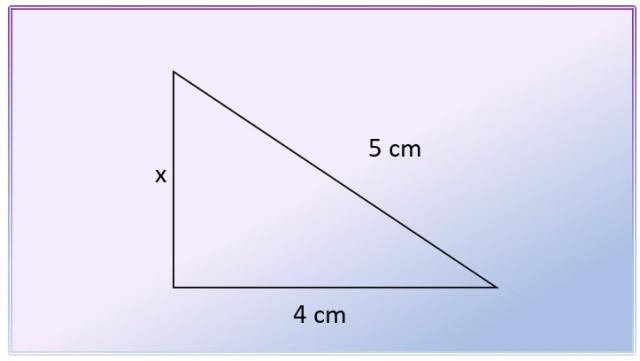
Si el perímetro del triángulo vale 12 cm, esto quiere decir que la suma de las medidas de los tres lados es igual a este valor:
x + 5 + 4 = 12
x + 9 =12
x = 12 – 9
x = 3
