Función biyectiva: qué es, cómo se hace, ejemplos, ejercicios

Una función biyectiva es aquella que cumple con la doble condición de ser inyectiva y sobreyectiva. Es decir, que todos los elementos del dominio tienen una única imagen en el codominio, y a su vez el codominio es igual al rango de la función ( R_f ).

Se cumple al plantearse una relación biunívoca entre los elementos del dominio y codominio. Un ejemplo simple es la función F : R → R definida por la recta F ( x ) = x

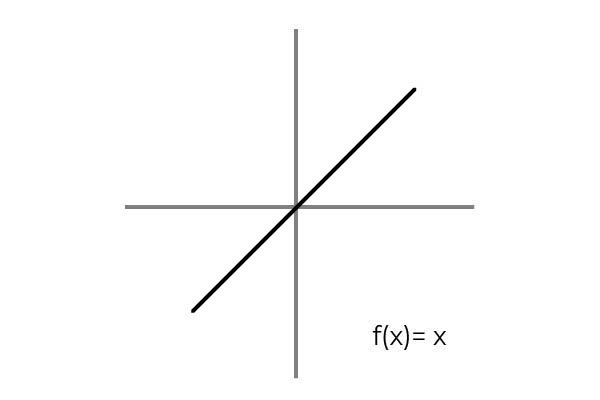
Se observa que para cada valor del dominio o conjunto de partida (ambos términos aplican por igual) se tiene una única imagen en el codominio o conjunto de llegada. Además no existe ningún elemento del codominio que no sea imagen.

De esta forma F : R → R definida por la recta F ( x ) = x  es biyectiva

Índice del artículo

• 1 ¿Cómo se hace una función biyectiva?
  • 1.1 Inyectividad de una función
  • 1.2 Sobreyectividad de una función
  • 1.3 Condicionamiento de funciones
• 2 Ejemplos: ejercicios resueltos
  • 2.1 Ejercicio 1
  • 2.2 Ejercicio 2
  • 2.3 Ejercicio 3
  • 2.4 Ejercicio 4
• 3 Ejercicios propuestos
• 4 Referencias

¿Cómo se hace una función biyectiva?

Para responder a esto es necesario tener claros los conceptos referentes a Inyectividad y Sobreyectividad de una función, además de los criterios para condicionar funciones en pro de adaptarlas a los requerimientos.

Inyectividad de una función

Una función es inyectiva cuando cada uno de los elementos de su dominio, está relacionado con un único elemento del codominio. Un elemento del codominio solo podrá ser imagen de un único elemento del dominio, de esta forma los valores de la variable dependiente no pueden repetirse.

Para considerar inyectiva a una función se debe cumplir lo siguiente:

∀ x₁  ≠ x₂   ⇒ F( x₁ ) ≠ F( x₂ )

Sobreyectividad de una función

Se clasifica a una función como sobreyectiva, si cada elemento de su codominio es imagen de al menos un elemento del dominio.

Para considerar sobreyectiva a una función se debe cumplir lo siguiente:

Sea F : D_f → C_f

∀ b ℮ C_f  E a  ℮  D_f   / F ( a ) = b

Esta es la manera algebraica para establecer que para todo “b” que pertenece a C_f existe un “a” que pertenece a D_f tal que, la función evaluada en “a” es igual a “b”. 

Condicionamiento de funciones

En ocasiones una función que no es biyectiva, puede someterse a ciertos condicionamientos. Estás nuevas condiciones pueden convertirla en una función biyectiva. Son válidos todo tipo de modificaciones al dominio y codominio de la función, donde el objetico es cumplir las propiedades de inyectividad y sobreyectividad en la relación correspondiente.

Ejemplos: ejercicios resueltos

Ejercicio 1

Sea la función F : R → R definida por la recta F ( x ) = 5x +1

R : [ Todos los números reales ]

Se observa que para todo valor del dominio existe una imagen en el codominio. Esta imagen es única lo cual hace de F sea una función inyectiva. De igual manera observamos que el codominio de la función es igual a su rango. Cumpliéndose así la condición de sobreyectividad.

Al ser inyectiva y sobreyectiva al mismo tiempo podemos concluir que

F : R → R definida por la recta F ( x ) = 5x +1 es una función biyectiva.

Esto aplica para todas las funciones lineales (Funciones cuyo mayor grado de la variable es uno).

Ejercicio 2

Sea la función F : R → R definida por F ( x ) = 3x² – 2

Al trazar una línea horizontal, se observa que la gráfica es encontrada en más de una ocasión. Debido a esto la función F no es inyectiva y por lo tanto no será biyectiva mientras esté definida en R → R

De igual manera existen valores del codominio que no son imágenes de ningún elemento del dominio. Debido a esto la función no es sobreyectiva, lo cual amerita condicionar también el conjunto de llegada.

Se procede a condicionar el dominio y codominio de la función

                                               F : [ 0 , ∞ ] → [ – 2 , ∞ ]

Donde se observa que el nuevo dominio abarca los valores desde el cero hasta el infinito positivo. Evitándose la repetición de valores que afecta a la inyectividad.

Así también el codominio ha sido modificado, contando a partir de “ -2 ” hasta el infinito positivo, eliminando del codominio los valores que no correspondían a ningún elemento del dominio

De esta forma se puede asegurar que F : [ 0 , ∞ ] → [ – 2 , ∞ ] definida por F ( x ) = 3x² – 2

Es biyectiva

Ejercicio 3

Sea la función F : R → R definida por F ( x ) = Sen ( x )

En el intervalo [ –∞ , +∞ ] la función seno varía sus resultados entre cero y uno.

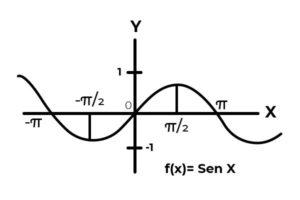
La función F no corresponde a los criterios de inyectividad y sobreyectividad, debido a que los valores de la variable dependiente se repiten cada intervalo de π. Además los términos del codominio fuera del intervalo [ -1 , 1 ] no son imagen de ningún elemento del dominio.

Al estudiar la gráfica de la función F ( x ) = Sen ( x ) se observan intervalos donde el comportamiento de la curva cumple con los criterios de biyectividad. Como por ejemplo el intervalo  D_f  = [  π/2  ,3π/2  ] para el dominio. Y C_f  = [ -1 , 1 ] para el codominio.

Donde la función varía resultados desde 1 hasta -1, sin repetir ningún valor en la variable dependiente. Y al mismo tiempo el codominio es igual a los valores adoptados por la expresión Sen ( x )

De esta forma la función F : [  π/2  ,3π/2  ] → [ -1 , 1 ]  definida por F ( x ) = Sen ( x ). Es biyectiva

Ejercicio 4

Plantee las condiciones necesarias para D_f y C_f. De manera que la expresión

F ( x ) = -x²  sea biyectiva.

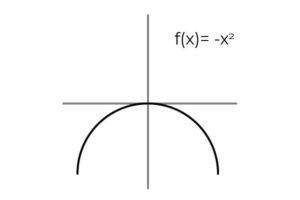
Se observa la repetición de resultados cuando la variable toma valores opuestos:

F ( 2 ) = F ( -2 ) = -4

F ( 3 ) = F ( -3 ) = -9

F ( 4 ) = F ( -4 ) = -16

Se condiciona el dominio, limitándolo al lado derecho de la recta real.

D_f = [ 0 , +∞ ]

De igual manera se observa que el rango de esta función es el intervalo [ –∞ , 0 ], el cual al fungir como codominio cumple las condiciones de sobreyectividad.

De esta forma podemos concluir que

La expresión F : [ 0 , +∞ ] → [ –∞ , 0 ] definida por F ( x ) = -x²   Es biyectiva

Ejercicios propuestos

Verificar si las siguientes funciones son biyectivas:

F : [ 0 , ∞ ) →R definida por F ( x ) = 3(x + 1)²  +2

F : [ 3π/2  ,5π/2  ] → R definida por F ( x ) = 5ctg ( x )

F : [ –π  ,π  ] → R definida por F ( x ) = Cos ( x – 3 )

F : R →R definida por la recta F ( x ) = -5x + 4

Referencias

1. Introduction to Logic and Critical Thinking. Merrilee H. Salmon. University of Pittsburgh
2. Problems in Mathematical Analysis. Piotr Biler, Alfred Witkowski. University of Wroclaw. Poland.
3. Elements of Abstract Analysis. Mícheál O’Searcoid PhD. Department of mathematics. University college Dublin, Beldfield, Dublind 4
4. Introduction to Logic and to the Methodology of the Deductive Sciences. Alfred Tarski, New York Oxford. Oxford University press.
5. Principios de análisis matemático. Enrique Linés Escardó. Editorial Reverté S. A 1991. Barcelona España.