Tipos de ángulos, características y ejemplos
Existen diversos tipos de ángulos, tomando en consideración varios criterios para diferenciarlos, por ejemplo se pueden distinguir a través de su medida, por la posición que ocupan y también de acuerdo a la suma con otros ángulos.
Usualmente un ángulo se define como la apertura comprendida entre dos semirrectas con un origen común, llamado el vértice del ángulo. La amplitud de la apertura es la medida del ángulo, que con frecuencia viene en grados o en radianes.
Un grado equivale a una de las 360 partes en que se puede dividir una circunferencia. Si se divide la circunferencia en dos partes iguales, cada una equivale a 180 grados o 180º, si en cambio se divide en cuatro partes iguales, cada una será de 90º y así sucesivamente. Este sistema se denomina sexagesimal.
Los radianes es otra medida muy empleada, que consiste en tomar una circunferencia y medir el ángulo entre dos de sus radios, cuya longitud es “r” y con el vértice en el centro de la circunferencia. De esta forma, el arco “s” entre dichos radios se hace valer “r” también y el ángulo subtendido entonces es de 1 radián o 1 rad y equivale a 57.3º grados.
El instrumento para medir ángulos es el transportador. Para tomar una medida se hace coincidir el centro del transportador con el vértice del ángulo y uno de los lados del mismo con la línea de 0º del transportador. El otro lado coincide con la medida del ángulo, que se lee en la escala.
Tipos de ángulos según su medida
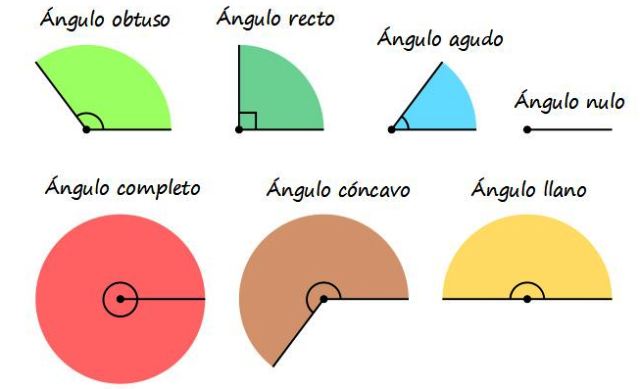
Una de las maneras más frecuentes de referirse a los ángulos es nombrarlos según su medida, aunque en algunas ocasiones un ángulo puede pertenecer a más de una categoría de las descritas seguidamente.
Ángulo nulo
Aquel cuya medida es 0º o 0 rad, es decir, las dos semirrectas tienen una apertura nula.
Ángulo agudo
La medida de un ángulo agudo se encuentra comprendida entre 0 y 90º o entre 0 y π/2 radianes. Por ejemplo, ángulos de 30º, 45º y 60º, que forman parte de los ángulos notables, son todos ellos ángulos agudos.
Ángulo recto
Es aquel que mide exactamente 90º (π/2 radianes), esto quiere decir que las semirrectas que lo definen son perpendiculares entre sí. Los ángulos internos de un cuadrado o de un rectángulo son ángulos rectos, y también es un ángulo recto el que se forma entre los catetos de un triángulo rectángulo.
Ángulo obtuso
Es un ángulo mayor que 90º o π/2 radianes.
Ángulo llano
Mide exactamente 180º, equivalente a π radianes. Cuando una magnitud vectorial es opuesta a otra, forman entre sí un ángulo de 180º, por ejemplo la velocidad de un móvil que se desplaza en línea recta y la desaceleración que experimenta cuando se está deteniendo.
Ángulo convexo
Siempre que un ángulo mida menos de 180º es un ángulo convexo. Un ángulo agudo puede ser convexo, al igual que uno de 90º y aquellos ángulos obtusos cuya medida esté comprendida en 90º y 180º. Más ejemplos de ángulos convexos son:
- 45º
- 60º
- 75º
- 135º
Ángulo cóncavo
Es el que mide más de 180º, como por ejemplo 225º o 270º, este último equivale a tres cuartas partes de la circunferencia.
Ángulo completo o perigonal
Su medida es 360º o 2π radianes. Significa que las dos semirrectas que lo conforman vuelven a coincidir, pero a diferencia del ángulo nulo, en este caso se ha dado una vuelta completa.
Tipos de ángulos según la posición de sus lados
En muchas figuras y estructuras geométricas aparece más de un ángulo y por eso es conveniente tener un criterio para comparar los lados de uno respecto a otro. De esta manera se tienen:
Ángulos consecutivos
Los ángulos consecutivos están uno al lado del otro, por lo tanto tienen un lado y un vértice común.
Ángulos adyacentes
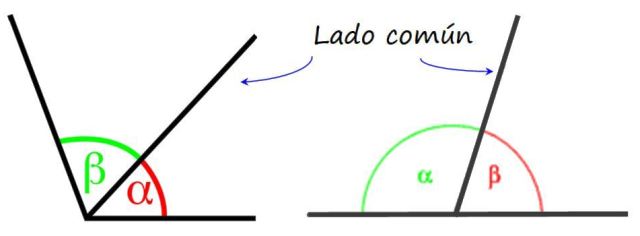
Los ángulos adyacentes tienen un lado y un vértice en común, es decir, se presentan uno al lado del otro. Pero a diferencia de los ángulos consecutivos, en los ángulos adyacentes los lados restantes son semirrectas opuestas, por lo tanto entre los dos ángulos suman 180º.
Ángulos opuestos por el vértice
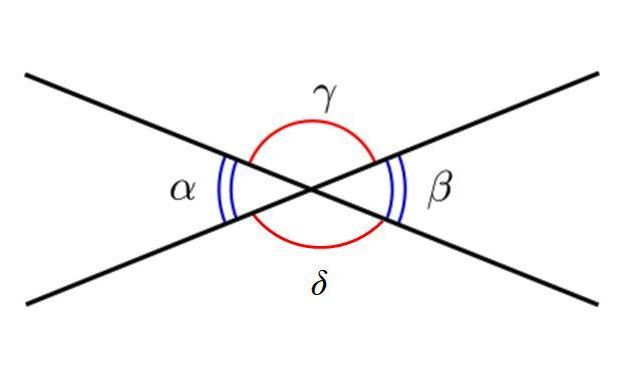
Los ángulos opuestos por el vértice tienen en común el vértice, y sus lados se prolongan opuestos, desde uno de los ángulos hasta el otro. De esta manera, los ángulos opuestos por el vértice tienen la misma medida.
En la siguiente figura se muestran 4 ángulos, denotados con letras griegas. Los ángulos azules son α y β, y como puede verse, son ángulos agudos y opuestos por el vértice. Por otro lado, los ángulos γ y δ son ángulos obtusos y también están opuestos por el vértice.
Tipos de ángulos según la suma de sus medidas
Algunos cálculos, sobre todo en trigonometría, se simplifican mucho observando si la suma de las medidas de dos ángulos es la de alguno de los ángulos notables, como el ángulo recto (90º) o el ángulo llano (180º). De acuerdo a ello se tienen:
Ángulos complementarios

Son complementarios aquellos ángulos cuya suma es igual a 90º. Por ejemplo, los ángulos agudos internos de un triángulo rectángulo son complementarios, ya que la suma de sus tres ángulos internos es igual a 180º.
Puesto que ya uno de los ángulos internos del triángulo rectángulo mide 90º, la suma de los otros dos también es igual a 90º.
Ángulos suplementarios
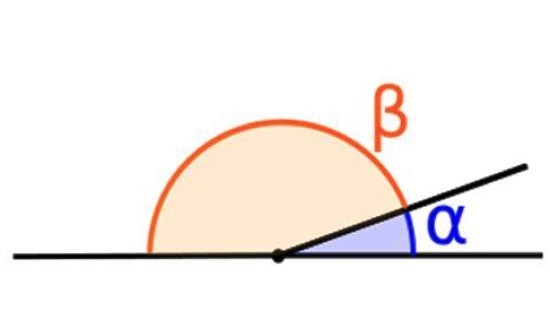
Son aquellos ángulos cuya suma es igual a 180º. Por ejemplo, los ángulos α y β mostrados en la figura superior.
Ejemplos de ángulos notables que a la vez son suplementarios son:
- 120º y 60º
- 135º y 45º
Referencias
- Alexander, D. 2013. Geometría. 5ta. Edición. Cengage Learning.
- Baldor. 1983. Geometría Plana y del Espacio y Trigonometría. Grupo Patria Cultural.
- E. A. 2003. Elementos de geometría: con ejercicios y geometría del compás. Universidad De Medellín.
- Geometría 1ro ESO. Ángulos en la circunferencia. Recuperado de: edu.xunta.es.
- Rich, B. Geometría. 1991. Serie Schaum. 2da. Edición. McGraw Hill.
