Experimento aleatorio: concepto, espacio muestral, ejemplos
Se habla de experimento aleatorio cuando el resultado de cada ensayo particular es impredecible, aun cuando se pueda establecer la probabilidad de ocurrencia de determinado resultado.
Sin embargo, habría que aclarar que no es posible reproducir el mismo resultado de un sistema aleatorio con los mismos parámetros y condiciones iniciales en cada ensayo del experimento.

Un buen ejemplo de un experimento aleatorio es el lanzamiento de un dado. Aun cuando se tenga el cuidado de lanzar el dado de la misma manera, en cada intento se obtendrá un resultado impredecible. Realmente, lo único que puede afirmarse es que el resultado puede ser alguno de los siguientes: 1, 2, 3, 4, 5 o 6.
El lanzamiento de una moneda, es otro ejemplo de experimento aleatorio con solo dos resultados posibles: cara o sello. Aunque la moneda se lance desde la misma altura y de la misma manera, siempre el factor azar estará presente, lo que resulta en incertidumbre a cada nuevo intento.
Lo contrario de un experimento aleatorio es un experimento determinista. Por ejemplo, se sabe que cada vez que se hierve agua a nivel del mar la temperatura de ebullición es 100 ºC. Pero nunca ocurre que, manteniendo las mismas condiciones, el resultado sea a veces 90 ºC, otras 12 0ºC y a veces 100 ºC.
Índice del artículo
El conjunto de todos los resultados posibles de un experimento aleatorio se denomina espacio muestral. En el experimento aleatorio del lanzamiento de un dado, el espacio muestral es:
D = {1, 2, 3, 4, 5, 6}.
Por su parte, en el lanzamiento de una moneda el espacio muestral es:
M ={cara, sello}.
En un experimento aleatorio, un evento es la ocurrencia o no de cierto resultado. Por ejemplo, en el caso del lanzamiento de una moneda, un evento o suceso es que salga cara.
Otro evento en un experimento aleatorio podría ser el siguiente: que en el lanzamiento de un dado salga un número menor o igual que tres.
En caso que se dé el evento, entonces el conjunto de resultados posibles es el conjunto:
E = {1, 2, 3}
A su vez, este es un subconjunto del espacio o conjunto muestral:
M = {1, 2, 3, 4, 5, 6}.
A continuación se presentan algunos ejemplos que ilustran lo antes dicho:
Suponga que se lanzan dos monedas, una a continuación de la otra. Se pide:
a) Indicar si se trata de un experimento aleatorio o por el contrario un experimento determinista.
b) ¿Cuál es el espacio muestral S de este experimento?
c) Indique el conjunto del evento A, correspondiente a que el experimento tenga como resultado cara y sello.
d) Calcule la probabilidad que se dé el evento A.
e) Finalmente, halle la probabilidad que se dé el evento B: no aparecer cara en el resultado.
Solución
a) Se trata de un experimento aleatorio porque no hay forma de predecir cuál será el resultado de un lanzamiento de las dos monedas.
b) El espacio muestral es el conjunto de todos los resultados posibles:
S = { (c, c), (c, s), (s, c), (s, s) }
c) El evento A, en el caso que se dé, puede tener los siguientes resultados:
A = { (c, s), (s, c) }
d) La probabilidad que se dé el evento A, se obtiene de dividir el número de elementos del conjunto A entre el número de elementos del conjunto S correspondiente al espacio muestral:
P(A) = 2/4 = ½ = 0.5 = 50%
e) El conjunto de resultados posibles correspondientes al evento B (no aparecer cara en el resultado) es:
B = { (s,s) }
Por lo que la probabilidad que se dé el evento B en un ensayo es el cociente entre el número de resultados posibles de B entre el número de casos totales:
P(B) = ¼ = 0.25 = 25%.
Una bolsa contiene 10 canicas blancas y 10 canicas negras. De la bolsa se sacan al azar y sin mirar adentro tres canicas consecutivamente.
a) Determine el espacio muestral de este experimento aleatorio.
b) Determine el conjunto de resultados correspondiente al evento A que consiste en que después del experimento se tengan dos canicas negras.
c) El evento B es obtener al menos dos canicas negras, determine el conjunto B de resultados para este suceso.
d) ¿Cuál es la probabilidad que se dé el evento A?
e) Halle la probabilidad que se dé el evento B.
f) Determine la probabilidad de que el resultado del experimento aleatorio sea que se tenga al menos una canica negra. A este evento se le denominará C.

Solución a
Para construir el espacio muestral, es útil confeccionar un diagrama de árbol, como el que se muestra en la figura 3:
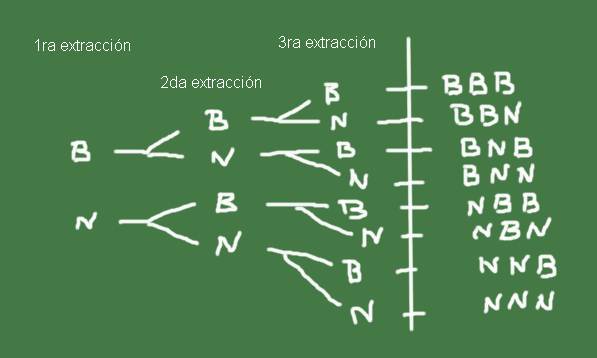
El conjunto Ω de posibles resultados de extraer tres canicas de una bolsa con igual número de canicas blancas y negras, es precisamente el espacio muestral de este experimento aleatorio.
Ω = { (b, b, b), (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, b), (n, n, n) }
Solución b
El conjunto de posibles resultados correspondiente al evento A, que consiste en tener dos canicas negras es:
A = { (b, n, n), (n, b, n), (n, n, b) }
Solución c
El suceso B se define como: “tener al menos dos canicas negras después de haber hecho la extracción al azar de tres de ellas”. El conjunto de resultados posibles para el evento B es:
B = { (b, n, n), (n, b, n), (n, n, b), (n, n, n) }
Solución d
La probabilidad de tener el evento A es el cociente entre el número de resultados posibles para este evento, y el número total de posibles resultados, es decir el número de elementos del espacio muestral.
P(A) = n(A) / n(Ω) = 3 / 8 = 0.375 = 37.5%
Entonces, hay 37.5% de probabilidad de tener dos canicas negras después de extraer al azar tres canicas de la bolsa. Pero obsérvese que de ninguna manera podemos predecir el resultado exacto del experimento.
Solución e
La probabilidad que se dé el evento B, consistente en que se obtenga al menos una canica negra es:
P(B) = n(B) / n(Ω) = 4 /8 = 0.5 = 50%
Esto significa que la posibilidad que se dé el evento B, es igual a la probabilidad que no se dé.
Solución f
La probabilidad de obtener al menos una canica negra, después de extraer tres de ellas, es igual a 1 menos la probabilidad de que el resultado sea “las tres canicas blancas”.
P(C) = 1 – P(b b b) = 1 – ⅛ = ⅞ = 0.875 = 87.5%
Ahora, podemos comprobar este resultado, notando que el número de posibilidades que se dé el evento C es igual al número de elementos de los posibles resultados para el evento C:
C = { (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, b), (n, n, n) }
n(C) = 7
P(C) = n(C) / n(Ω) = ⅞ = 87.5%
- CanalPhi. Experimento aleatorio. Recuperado de: youtube.com.
- MateMovil. Experimento aleatorio. Recuperado de: youtube.com
- Pishro Nick H . Introduction to probability. Recuperado de:probabilitycourse.com
- Ross. Probabilidad y estadistica para ingenieros. Mc-Graw Hill.
- Wikipedia. Experiment (probability theory). recuperado de: en.wikipedia.com
- Wikipedia. Suceso determinista. Recuperado de: es. wikipedia.com
- Wikipedia. Experimento aleatorio. Recuperado de: es.wikipedia.com
