Sistema de coordenadas rectangulares: qué es, para qué sirve, ejemplos
¿Qué es el sistema de coordenadas rectangulares?
En matemática y geometría, un sistema de coordenadas rectangulares sirve para ubicar de manera precisa cualquier punto sobre el espacio. Para ello es suficiente con dar tres coordenadas.
La construcción del sistema en el plano es muy simple, solo se necesitan tres rectas que serán los ejes coordenados o ejes cartesianos: uno vertical, otro horizontal y un tercero que entra o sale del papel o la pantalla.
Dichos ejes son mutuamente perpendiculares y el punto de intersección es el origen del sistema.
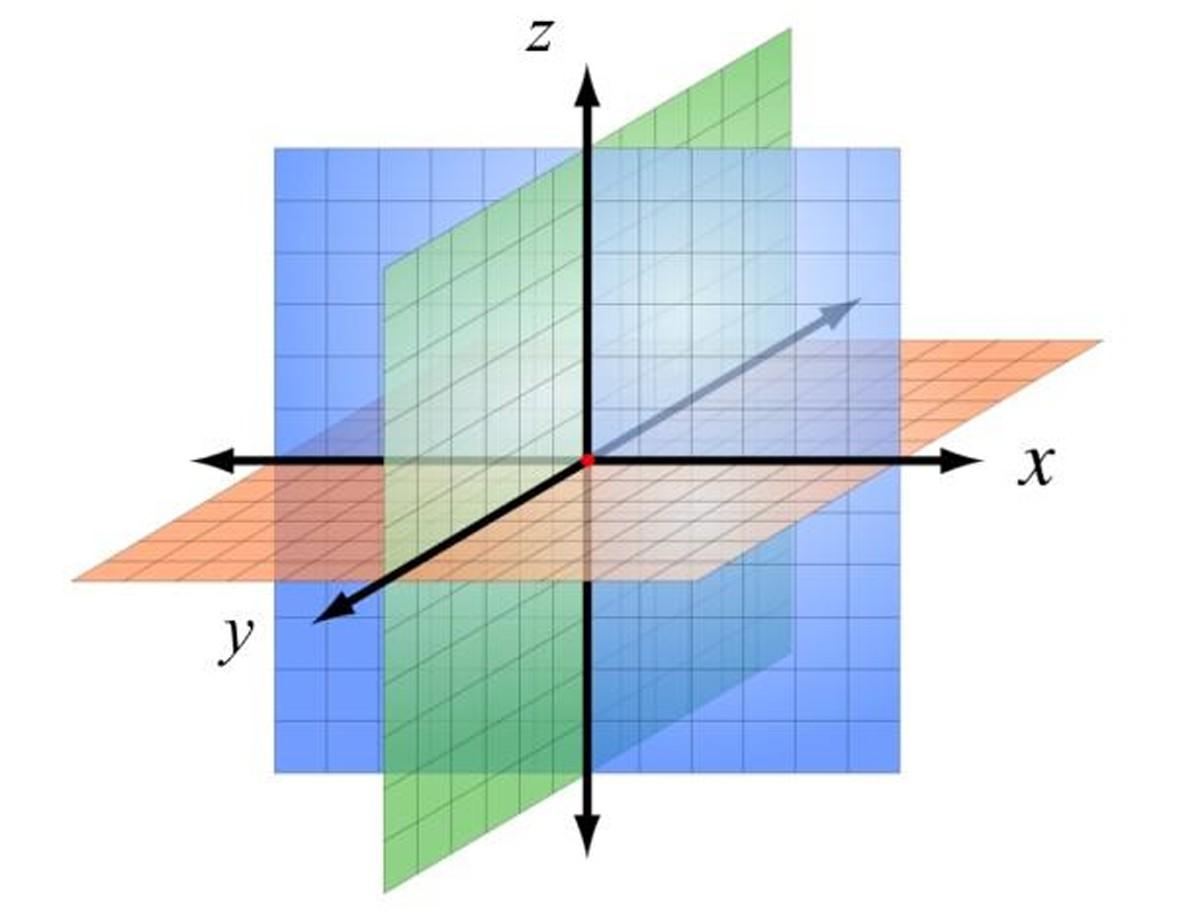
Esta disposición se muestra en la figura de arriba, en la cual se han asignado a los ejes coordenados las letras x, y, z, para distinguirlos. De esta forma se determinan tres planos, con el origen coloreado en rojo.
El plano xz, en color azul, es el plano de la pantalla y está frente a los ojos del lector. El plano xy es de color naranja, y se puede asociar con la mesa o el suelo. Por último, el plano zy en verde es perpendicular a los anteriores y secciona la pantalla o el papel en dos regiones.
Cuadriculando cada uno de estos planos y asignando una escala, se puede ubicar cualquier punto en el espacio dando las respectivas coordenadas x, y, z, siempre en ese orden, para evitar ambigüedades.
¿Para qué sirve el sistema de coordenadas rectangulares?
El sistema de coordenadas rectangulares sirve para posicionar cualquier punto en el espacio o en el plano, bastando para ello indicar las tres coordenadas del punto, en el orden x, y, z.
Si el punto pertenece a un plano, una de las coordenadas será 0 y si está sobre alguno de los ejes, dos de las coordenadas serán 0, excepto aquella que corresponda a la ubicación del punto, salvo el origen, que, como se dijo antes, tiene coordenadas (0,0,0).
Los siguientes ejemplos aclaran lo antes expuesto.
Ejemplos
Ejemplo 1
Un punto P cualquiera sobre el eje x se expresa a través de las coordenadas P (x, 0, 0). Obsérvese que el origen, destacado en rojo en la siguiente figura, tiene coordenadas O (0, 0, 0).
Cuando el punto está a la derecha del origen, tiene coordenada x positiva, mientras que si está a la izquierda, es negativa. Por ejemplo, el punto P1 en azul tiene coordenadas (6,0,0), mientras que el punto P2 en verde, tiene coordenadas (-9,0,0).

Ejemplo 2
En la siguiente figura hay dos ejes, siendo el eje x el eje horizontal y el eje y el vertical. Con esto es suficiente para representar puntos en el plano, siendo necesarias dos coordenadas. El origen O es el punto (0,0).
Nótese que la disposición de los ejes divide al plano en cuatro regiones llamadas cuadrantes. A los ejes por encima y a la derecha del origen se les designa con signo positivo, mientras que por debajo y a la izquierda se les distingue con signo negativo.
Entonces, los puntos cuyas coordenadas son positivas ambas, corresponden al primer cuadrante o cuadrante I. El punto verde tiene coordenadas (2,3) y está en el I cuadrante.
Por su parte, el punto rojo tiene coordenadas (-3,1) y está en el II cuadrante, mientras que las coordenadas del punto azul son (-1.5;-2.5) y está en el III cuadrante.

Ejemplo 3
El siguiente es un ejemplo de punto en el espacio. Sus coordenadas son x = 6, y = 10 y z = 8, por lo tanto, P (6,10,8).
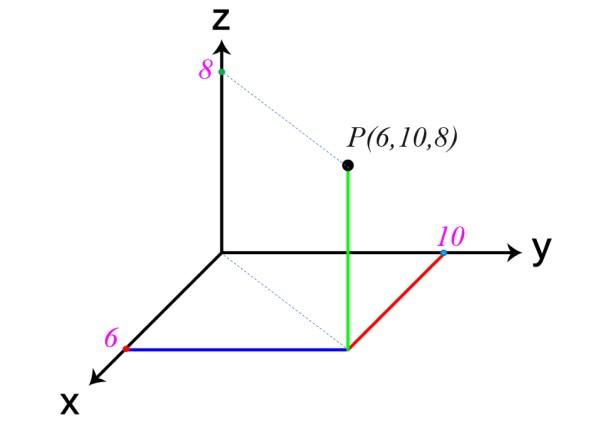
En la figura del comienzo, se advierte que los planos xy, xz y zy dividen el espacio en ocho regiones, llamadas octantes. El punto P del ejemplo se encuentra en el primer octante.
Referencias
- Alexander, D. (2013). Geometría. 5ta. Edición. Cengage Learning.
- Larson, R. (2012). Precálculo. 8va. Edición. Cengage Learning.
- Stewart, J. (2007). Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
- The Cartesian Plane. Recuperado de: dl.uncw.edu.
- Weisstein, E. Cartesian Coordinates. Recuperado de: mathworld.wolfram.com
