Método de Euler: para qué sirve, procedimiento y ejercicios
El método de Euler es el más básico y sencillo de los procedimientos usados para encontrar soluciones numéricas aproximadas, a una ecuación diferencial ordinaria de primer orden, siempre que se conozca su condición inicial.
Una ecuación diferencial ordinaria (EDO) es la ecuación que relaciona una función desconocida de una sola variable independiente con sus derivadas.
Si la mayor derivada que aparece en la ecuación es de grado uno, entonces se trata de una ecuación diferencial ordinaria de primer grado.
La forma más general de escribir una ecuación de primer grado es:
x = x0
y = y0
Índice del artículo
- 1 ¿En que consiste el método de Euler?
- 2 Ejercicios resueltos
- 3 Dinámica de Newton y el método de Euler
- 4 Ejercicios propuestos para casa
- 5 Referencias
La idea del método de Euler es encontrar una solución numérica a la ecuación diferencial en el intervalo comprendido entre X0 y Xf .
En primer lugar se discretiza el intervalo en n+1 puntos:
x0, x1, x2, x3…, xn
Los cuales se obtienen así:
xi=x0+ih
Donde h es el ancho o paso de los subintervalos:
Con la condición inicial, entonces es posible también conocer la derivada al inicio:
y’ (xo) = f (xo, yo)
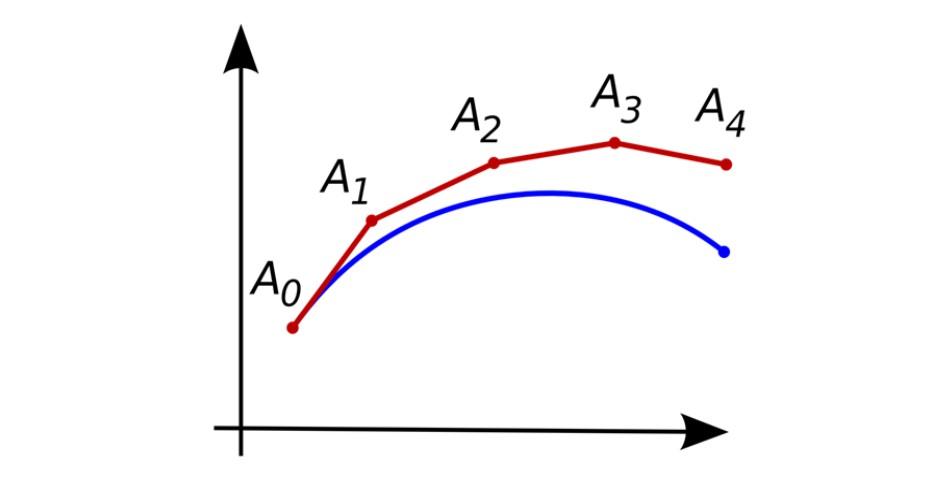
Esta derivada representa la pendiente de la recta tangente a la curva de la función y(x) precisamente en el punto:
Ao = (xo, yo)
Entonces se hace una predicción aproximada del valor de la función y(x) en el punto siguiente :
y (x1) ≈ y1
y1 = yo +(x1– xo) f (xo, yo) = yo + h f (xo, yo)
Se ha obtenido entonces el próximo punto aproximado de la solución que correspondería a:
A1 = (x1, y1)
El procedimiento se repite para obtener los sucesivos puntos
A2, A3…, xn
En la figura mostrada al comienzo, la curva azul representa la solución exacta de la ecuación diferencial, y la roja representa los sucesivos puntos aproximados obtenidos por el procedimiento de Euler.
I) Sea la ecuación diferencial:
Con la condición inicial x=a= 0 ; ya= 1
Mediante el uso del método de Euler consiga una solución aproximada de y en la coordenada X = b = 0.5, subdividiendo el intervalo [a , b] en n = 5 partes.
Solución

Los resultados numéricos quedan resumidos así:

De donde se concluye que la solución Y para el valor 0.5 es 1.4851.
Nota: para la realización de los cálculos se ha usado Smath Studio, programa gratuito de uso libre.
II) Continuando con la ecuación diferencial del ejercicio I), halle la solución exacta y compárela con el resultado obtenido por el método de Euler. Encuentre el error o diferencia entre el resultado exacto y el aproximado.
Solución
La solución exacta no es muy difícil de encontrar. Se sabe que la derivada de la función sen(x) es la función cos(x). Por lo tanto la solución y(x) será:
y(x) = sen x + C
Para que se cumpla la condición inicial y(0) = 1, la constante C debe valer 1. A continuación se compara el resultado exacto con el aproximado:

Se concluye que en el intervalo calculado, la aproximación tiene tres cifras significativas de precisión.
III) Considere la ecuación diferencial y sus condiciones iniciales dadas a continuación:
y''(x) =- y2
Con la condición inicial x0 = 0; y0 = 1
Use el método de Euler para encontrar valores aproximados de la solución y(x) en el intervalo x = [0 , 1.5 ]. Utilice paso h=0.1.
Solución
El método de Euler es muy indicado para ser usado con una hoja de cálculo. En este caso usaremos la hoja de cálculo de geogebra, un programa gratuito y de uso libre.
En la hoja de cálculo de la figura se muestran tres columnas (A,B,C) la primera es la variable x , la segunda columna representa la variable y, y la tercera columna la derivada y’.
La fila 2 contiene los valores iniciales de X, Y, Y’ .
El paso de valor 0.1 se ha colocado en la celda de posición absoluta ($D$4).
El valor inicial de y0 está en la celda B2, y y1 en la celda B3. Para calcular y1 se usa la fórmula:
y1 = yo +(x1– xo) f (xo, yo) = yo + h f (xo, yo)
Esta fórmula en hoja de cálculo sería Número B3: =B2 + $D$4 * C3.
De modo similar y2 estaría en la celda B4 y su fórmula se muestra en la figura siguiente:
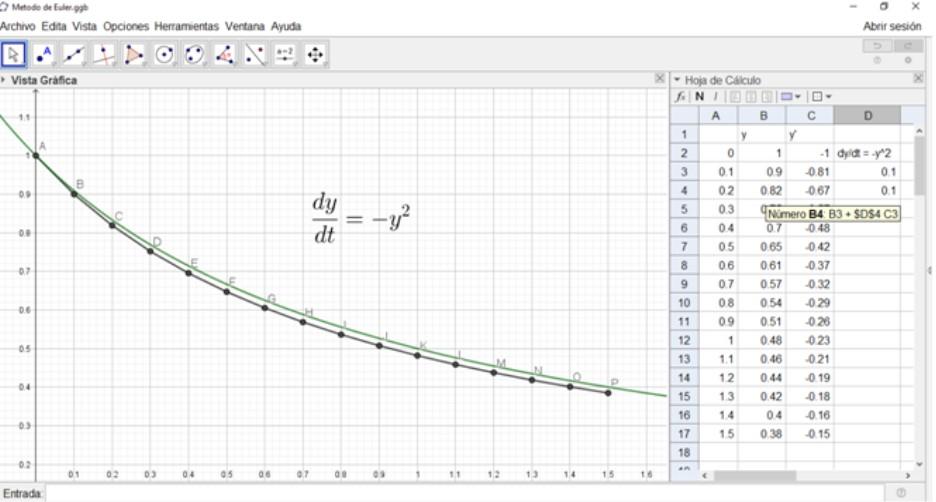
La figura muestra también la gráfica de la solución exacta, y los puntos A, B, …, P de la solución aproximada mediante el método de Euler.
La dinámica clásica fue desarrollada por Isaac Newton (1643 – 1727). La motivación original de Leonard Euler (1707 – 1783) para desarrollar su método, fue precisamente el de resolver la ecuación de la segunda ley de Newton en diversas situaciones físicas.
La segunda ley de Newton suele expresarse como una ecuación diferencial de segundo grado:
Donde x representa la posición de un objeto en el instante t. Dicho objeto tiene una masa m y está sometido a una fuerza F. La función f se relaciona con la fuerza y la masa de la siguiente manera:
Para aplicar el método de Euler se requiere de los valores iniciales de tiempo t, velocidad v y posición x.
El siguiente cuadro explica como partiendo de valores iniciales t1, v1, x1 puede obtenerse una aproximación de la velocidad v2 y la posición x2, en el instante t2=t1+Δt, donde Δt representa un pequeño incremento y corresponde al paso en el método de Euler.

IV) Uno de los problemas fundamentales en mecánica es el de un bloque de masa M atado a un muelle (o resorte) de constante elástica K.
La segunda ley de Newton para este problema sería así:
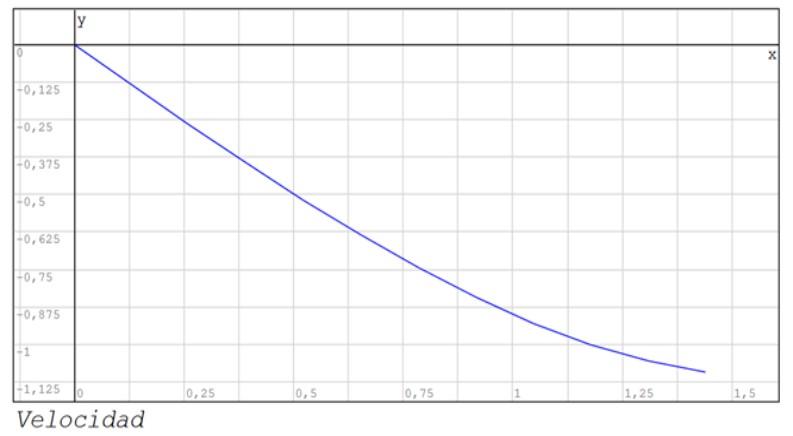
En este ejemplo, para simplificar se tomará M=1 y K=1. Encuentre soluciones aproximadas a la posición x y la velocidad v por el método de Euler en el intervalo de tiempo [0 , π/2 ] subdividiendo el intervalo en 12 partes.
Tome 0 como instante inicial, velocidad inicial 0 y posición inicial 1.
Solución
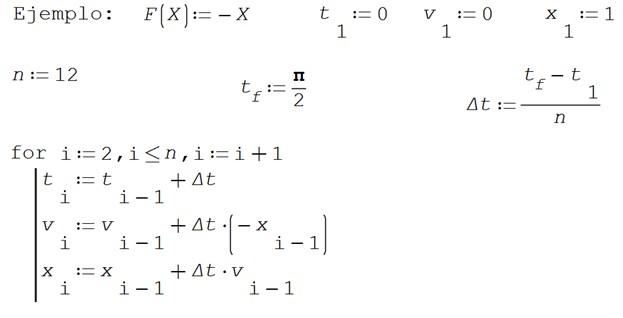
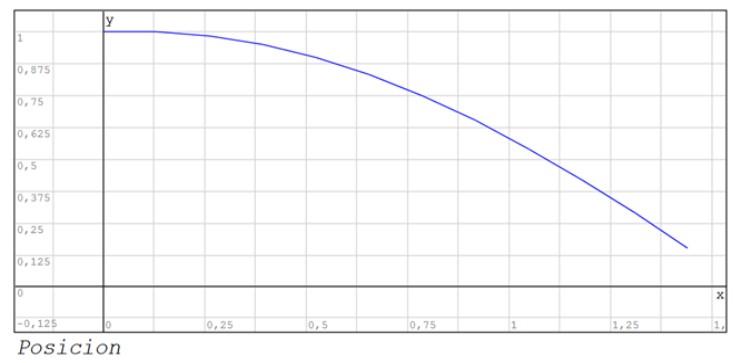
Los resultados numéricos se muestran en el cuadro siguiente:

También se muestran los gráficos de la posición y la velocidad entre los instantes 0 y 1.44.
Use una hoja de cálculo para determinar una solución aproximada mediante el método de Euler para la ecuación diferencial:
y’ = – Exp( -y) con las condiciones iniciales x=0, y=-1 en el intervalo x =[0 , 1]
Comience con un paso de 0,1. Grafique el resultado.
Mediante el uso de una hoja de cálculo encuentre soluciones numéricas a la siguiente ecuación de segundo grado, en donde y es función de la variable independiente t.
y’’ = – 1/y² con la condición inicial t=0 ; y(0)= 0,5 ; y’(0)=0
Encuentre la solución en el intervalo [0,5 ; 1,0] usando un paso de 0,05.
Grafique el resultado: y vs t ; y’ vs t
- Método de Eurler.Tomado de wikipedia.org
- Euler solver. Tomado de en.smath.com
