Datos no agrupados: ejemplos y ejercicio resuelto
Los datos no agrupados son aquellos que, obtenidos a partir de un estudio, no están todavía organizados por clases. Cuando es un número manejable de datos, usualmente 20 o menos, y hay pocos datos diferentes, se pueden tratar como no agrupados y extraer información valiosa de ellos.
Los datos no agrupados provienen tal cual de la encuesta o del estudio realizado para obtenerlos y por ello carecen de procesamiento. Veamos algunos ejemplos:

-Resultados de un examen de coeficiente intelectual CI realizado a 20 alumnos al azar de una universidad. Los datos obtenidos fueron los siguientes:
119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112,106
-Edades de 20 empleados de cierta cafetería muy popular:
24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 21, 22, 23, 21, 19, 22, 27, 29, 23, 20
-El promedio de notas finales de 10 alumnos de una clase de Matemática:
3,2; 3,1; 2,4; 4,0; 3,5; 3,0; 3,5; 3,8; 4,2; 4,9
Índice del artículo
- 1 Propiedades de los datos
- 2 Cálculo de la media, la mediana y la moda
- 3 Rango, varianza, desviación estándar y sesgo
- 4 Ejercicio resuelto
- 5 Referencias
Hay tres propiedades importantes que caracterizan a un conjunto de datos estadísticos estén o no agrupados, las cuales son:
-Posición, que es la tendencia de los datos a agruparse en torno a determinados valores.
-Dispersión, un indicativo de cuán dispersos o diseminados se encuentran los datos en torno a un valor determinado.
-Forma, se refiere a la forma en que están distribuidos los datos, la cual se aprecia cuando se construye una gráfica de los mismos. Hay curvas muy simétricas y también sesgadas, ya sea a la izquierda o hacia la derecha de cierto valor central.
Para cada una de estas propiedades hay una serie de medidas que las describen. Una vez obtenidas, nos brindan un panorama del comportamiento de los datos:
-Las medidas de posición más utilizadas son la media aritmética o simplemente media, la mediana y la moda.
-En la dispersión se utilizan frecuentemente el rango, la varianza y la desviación estándar, pero no son las únicas medidas de dispersión.
-Y para determinar la forma, se comparan la media y la mediana a través del sesgo, como se verá en breve.
–La media aritmética, también conocida como promedio y denotada como X, se calcula de la siguiente forma:
X = (x1 + x2 + x3 + ….. xn) / n
Donde x1, x2, …. xn, son los datos y n es el total de ellos. En notación de sumatoria se tiene:
–La mediana es el valor que aparece en el medio de una sucesión ordenada de datos, así que para obtenerla, es preciso ordenar los datos antes que nada.
Si el número de observaciones es impar, no hay problema en encontrar el punto medio del conjunto, pero si tenemos número par de datos, se buscan los dos datos centrales y se los promedia.
–La moda es el valor más común que se observa en el conjunto de datos. No siempre existe, puesto que es posible que ningún valor se repita con mayor frecuencia que otro. También pudiera haber dos datos con igual frecuencia, en cuyo caso se habla de una distribución bi-modal.
A diferencia de las dos medidas anteriores, la moda se puede usar con datos cualitativos.
Veamos cómo se calculan estas medidas de posición con un ejemplo:
Ejemplo resuelto
Supongamos que se quiere determinar la media aritmética, la mediana y la moda en el ejemplo propuesto al comienzo: las edades de 20 empleados de una cafetería:
24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 21, 22, 23, 21, 19, 22, 27, 29, 23, 20
La media se calcula simplemente sumando todos los valores y dividiendo entre n = 20, que es el número total de datos. De esta manera:
X = (24 + 20 + 22 + 19 + 18 + 27+ 25 + 19 + 27 + 18 + 21 + 22 + 23 + 21+ 19 + 22 + 27+ 29 + 23+ 20) / 20 =
= 22.3 años.
Para hallar la mediana es necesario ordenar primero el conjunto de datos:
18, 18, 19, 19, 19, 20, 20, 21, 21, 22, 22, 22, 23, 23, 24, 25, 27, 27, 27, 29
Como es un número par de datos, se toman los dos datos centrales, resaltados en negrita, y se promedian. Debido a que ambos son 22, la mediana es de 22 años.
Por último, la moda es el dato que más se repite o aquel cuya frecuencia es mayor, siendo este 22 años.
El rango es simplemente la diferencia entre el mayor y el menor de los datos y permite apreciar rápidamente la variabilidad de ellos. Pero aparte, hay otras medidas de dispersión que ofrecen más información acerca de la distribución de los datos.
La varianza se denota como s y se calcula mediante la expresión:
Entonces para interpretar acertadamente los resultados, se define la desviación estándar como la raíz cuadrada de la varianza, o también la cuasi-desviación estándar, que es la raíz cuadrada de la cuasivarianza:
Es la comparación entre la media X y la mediana Med:
-Si Med = media X: los datos son simétricos.
-Cuando X > Med: sesgamiento hacia la derecha.
-Y si X Med: los datos sesgan hacia la izquierda.
Encontrar media, mediana, moda, rango, varianza, desviación estándar y sesgo para los resultados de un examen de coeficiente intelectual realizado a 20 alumnos de una universidad:
119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112, 106
Ordenaremos los datos, ya que será necesario para encontrar la mediana.
106, 106, 106, 109, 109, 109, 109, 109, 112, 112, 112, 112, 112, 112, 112, 119, 119, 124, 124, 124
Y los pondremos en una tabla como sigue, para facilitar los cálculos. La segunda columna titulada “Acumulado” es la suma del dato correspondiente más el anterior.
Esta columna ayudará a encontrar fácilmente la media, dividiendo el último acumulado entre el número total de datos, como se ve al final de la columna de “Acumulado”:
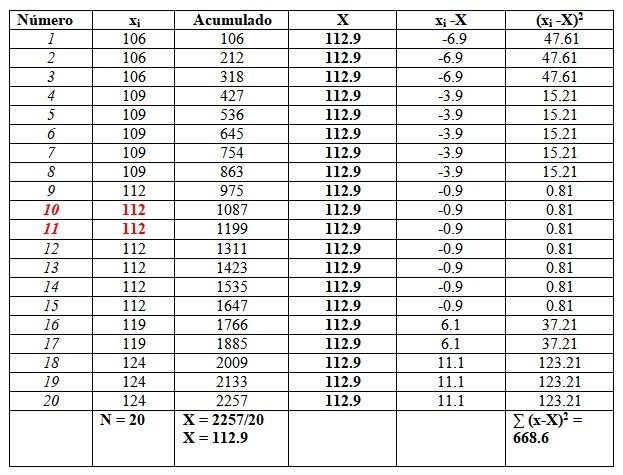
X = 112.9
La mediana es el promedio de los datos centrales resaltados en rojo: el número 10 y el número 11. Como son iguales, la mediana es 112.
Por último, la moda es el valor que más se repite y es 112, con 7 repeticiones.
En cuanto a las medidas de dispersión, el rango es:
124-106 = 18.
La varianza se obtiene dividiendo el resultado final de la columna derecha entre n:
s = 668.6/20 = 33.42
En este caso, la desviación estándar es la raíz cuadrada de la varianza: √33.42 = 5.8.
Por su parte, los valores de la cuasivarianza y la cuasi desviación estándar son:
sc=668.6/19 = 35.2
Cuasi-desviación estándar = √35.2 = 5.9
Por último, el sesgo es ligeramente hacia la derecha, ya que la media 112.9 es mayor que la mediana 112.
- Berenson, M. 1985. Estadística para administración y economía. Interamericana S.A.
- Canavos, G. 1988. Probabilidad y Estadística: Aplicaciones y métodos. McGraw Hill.
- Devore, J. 2012. Probability and Statistics for Engineering and Science. 8th. Edition. Cengage.
- Levin, R. 1988. Estadística para Administradores. 2da. Edición. Prentice Hall.
- Walpole, R. 2007. Probabilidad y Estadística para Ingeniería y Ciencias. Pearson.
