¿Qué son los Ángulos Alternos Internos? (Con Ejercicios)
Los ángulos alternos internos son aquellos ángulos formados por la intersección de dos rectas paralelas y una recta transversal. Cuando una recta L1 es cortada por una recta transversal L2 se forman 4 ángulos.
Los dos pares de ángulos que quedan del mismo lado de la recta L1 son llamados ángulos suplementarios, puesto que su suma es igual a 180º. En la imagen inferior los ángulos 1 y 2 son suplementarios, al igual que los ángulos 3 y 4.
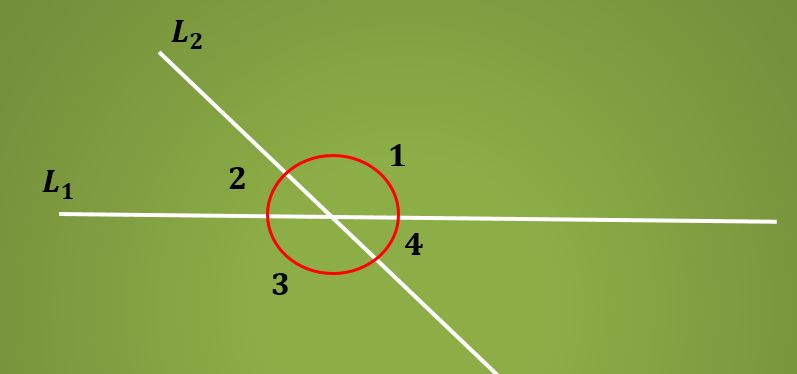
Para poder hablar de ángulos alternos internos es necesario tener dos rectas paralelas y una recta transversal; según lo visto antes, se formarán ocho ángulos.
Cuando se tienen dos rectas paralelas L1 y L2 cortadas por una recta transversal se forman ocho ángulos, como se ilustra en la siguiente imagen.
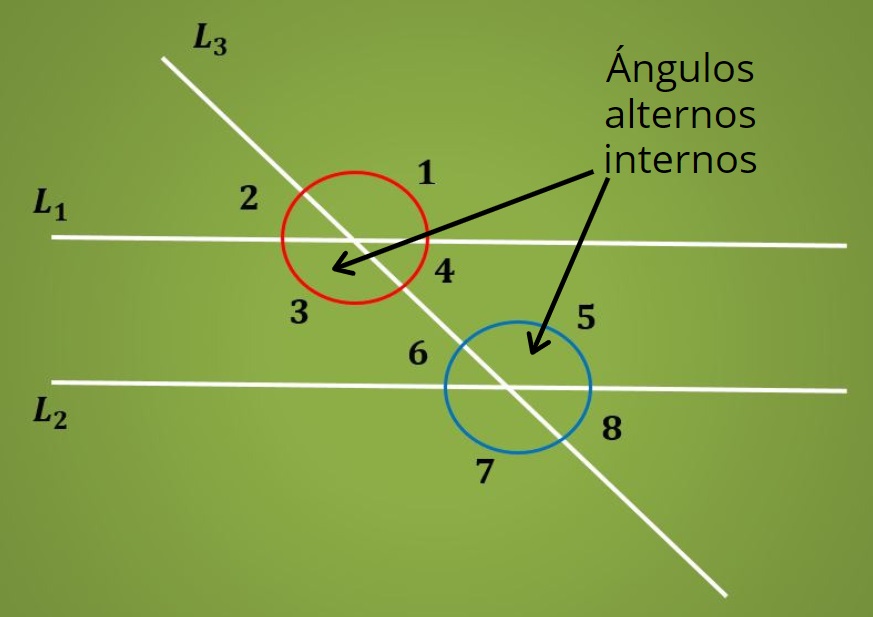
En la imagen superior los pares de ángulos 1 y 2, 3 y 4, 5 y 6, 7 y 8 son ángulos suplementarios.
Ahora, los ángulos alternos internos son los que se encuentran entre las dos rectas paralelas L1 y L2, pero están ubicados a lados opuestos de la recta transversal L2. Es decir, que los ángulos 3 y 5 son alternos internos. Del mismo modo, los ángulos 4 y 6 son ángulos alternos internos.
Ángulos opuestos por el vértice
Para saber la utilidad que tienen los ángulos alternos internos es necesario primero saber que si dos ángulos son opuestos por el vértice, entonces estos dos ángulos miden lo mismo.
Por ejemplo, los ángulos 1 y 3 miden lo mismo al ser opuestos por el vértice. Bajo el mismo razonamiento se puede concluir que los ángulos 2 y 4, 5 y 7, 6 y 8 miden lo mismo.
Ángulos formados entre una secante y dos paralelas
Cuando se tienen dos rectas paralelas cortadas por una recta secante o transversal como en la figura anterior, se cumple que los ángulos 1 y 5, 2 y 6, 3 y 7, 4 y 8 miden lo mismo.
Ángulos alternos internos
Utilizando la definición de ángulos puestos por el vértice y la propiedad de los ángulos formados entre una secante y dos rectas paralelas, se puede concluir que los ángulos alternos internos tienen la misma medida.
Ejercicios resueltos
– Primer ejercicio
Calcular la medida del ángulo 6 de la siguiente imagen, sabiendo que el ángulo 1 mide 125º.
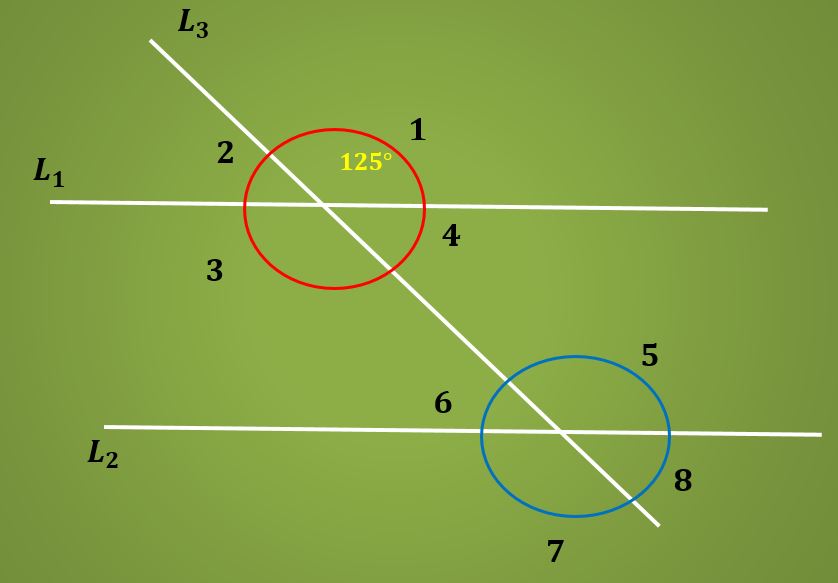
Solución
Ya que los ángulos 1 y 5 son opuestos por el vértice, se tiene que el ángulo 3 mide 125º. Ahora, como los ángulos 3 y 5 son alternos internos, se tiene que el ángulo 5 mide también 125º.
Finalmente, como los ángulos 5 y 6 son suplementarios, se tiene que la medida del ángulo 6 es igual a 180º – 125º = 55º.
– Segundo ejercicio
Calcular le medida del ángulo 3 sabiendo que el ángulo 6 mide 35º.
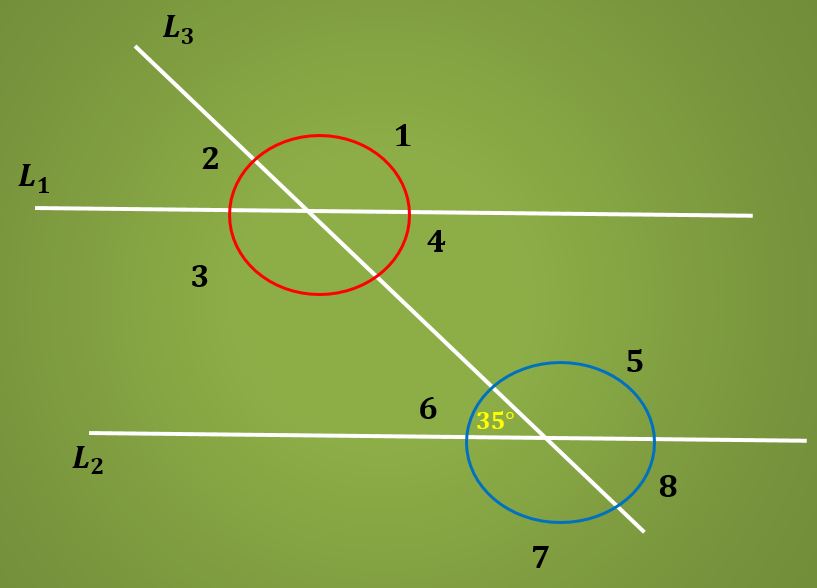
Solución
Se sabe que el ángulo 6 mide 35º, y además se sabe que los ángulos 6 y 4 son alternos internos, por lo tanto miden lo mismo. Es decir que el ángulo 4 mide 35º.
Por otro lado, utilizando el hecho de que los ángulos 4 y 3 son suplementarios, se tiene que la medida del ángulo 3 es igual a 180º – 35º = 145º.
Observación
Es necesario que las rectas sean paralelas para que puedan cumplir las propiedades correspondientes.
Los ejercicios quizás puedan resolverse más rápido, pero en este artículo se quiso utilizar la propiedad de los ángulos alternos internos.
Referencias
- Bourke. (2007). An Angle on Geometry Math Workbook. NewPath Learning.
- Clemens, S. R., O’Daffer, P. G., & Cooney, T. J. (1998). Geometría. Pearson Educación.
- Lang, S., & Murrow, G. (1988). Geometry: A High School Course. Springer Science & Business Media.
- Lira, A., Jaime, P., Chavez, M., Gallegos, M., & Rodríguez, C. (2006). Geometria y Trigonometria. Ediciones Umbral.
- Moyano, A. R., Saro, A. R., & Ruiz, R. M. (2007). Álgebra y Geometría Cuadrática. Netbiblo.
- Sullivan, M. (1997). Trigonometría y geometría analítica. Pearson Educación.
- Wingard-Nelson, R. (2012). Geometry. Enslow Publishers, Inc.
