Variable aleatoria discreta: qué es, características, ejemplos, ejercicios
¿Qué es una variable aleatoria discreta?
Una variable aleatoria discreta es un valor numérico obtenido al azar, como resultado de un experimento y que solo toma valores finitos o contables. Esto significa que, dados dos valores consecutivos de la variable, no existe un valor intermedio entre ellos.
Ejemplos de variables discretas son el número de pétalos de una flor, cuantas caras (o cruces) resultan de lanzar simultáneamente dos monedas, la cantidad de integrantes o de hijos de una familia, número de personas viviendo en una casa y muchas más.
En todos los casos, los resultados de llevar a cabo el experimento son contables. Se puede definir una variable aleatoria llamada “X = número de hijos de una familia”, y esta variable puede tomar los valores 0, 1, 2, 3…
De modo que, para un caso general, una variable aleatoria discreta se identifica mediante:
X = {x1, x2, x3… xk}
Donde x1, x2, x3… son los posibles resultados del experimento.
Con frecuencia, interesa conocer la probabilidad de ocurrencia de cada uno de estos posibles resultados, denotada como:
p1 = P (X = x1)
p2 = P (X = x2)
.
.
.
Y así sucesivamente para cada valor de X. El índice “i”, varía desde 1 hasta k: i=1,2,3…k.
Esta lista, que contiene las probabilidades de cada resultado posible del experimento, se denomina distribución de probabilidad o función de probabilidad, siempre que la variable aleatoria sea numérica, la probabilidad de cada suceso esté comprendida entre 0 y 1 y la suma de todas las probabilidades sea igual a 1.
Ejemplos de variables aleatorias discretas
Las variables aleatorias discretas siempre son numéricas y contables. Por lo general miden el número de veces que ocurre un suceso, por ejemplo:
- Número de llamadas recibidas por un centro de llamadas en una tarde.
- Cantidad de depósitos bancarios efectuados en un solo día.
- Lanzar un dado y leer el número que aparece en la cara superior.
- Número de caras que salen al lanzar dos monedas idénticas.
- Alumnos que aprobaron el examen de Álgebra I, seleccionados al azar de un grupo de 100 estudiantes de ingeniería de una universidad.
- Integrantes adultos de una manada de elefantes en una reserva de África.
- Número de hijos por familia en una determinada ciudad.
- Personas que asisten a una función de cine de medianoche.
- Cantidad de automóviles que pasan por un peaje de una autopista.
Valores enteros y fraccionarios
Todas las variables aleatorias discretas mencionadas toman valores enteros. Sin embargo, se pueden definir variables aleatorias discretas con valores fraccionarios, por ejemplo, la variable aleatoria F dada por:
F = {fracción de piezas defectuosas al escoger al azar 50 elementos de un lote}
Los posibles valores son los siguientes:
- No se encuentre ninguna pieza defectuosa: f1=0
- Solo 1 pieza defectuosa de 50: f2=1/50 = 0.02
- Se encuentren dos piezas defectuosas en 50: f3=2/50 = 0.04
- Y así sucesivamente, hasta llegar al caso en que las 50 piezas elegidas estén malas: f51 = 50/50=1
Ejercicios resueltos
Ejercicio 1: identificar variables aleatorias discretas
Se tienen las variables aleatorias dadas por:
X= {Número de sismos al año, ocurridos en una determinada zona geográfica}
Y = {Longitud exacta del pie humano}
Z = {Talla de calzado para adultos}
R = {Tiempo de duración de una llamada a un call center}
¿Son todas ellas variables aleatorias discretas? Justificar la respuesta.
Solución
Las variables X y Z son discretas, ya que el número de sismos ocurridos en un año es una cantidad contable. Por otra parte, las tallas de calzado son finitas, la numeración puede variar según el país, por ejemplo 6, 6.5, 7…, pero igualmente es una cantidad finita.
En cambio, la longitud exacta del pie humano puede tomar cualquier cualquier valor. Por ejemplo, entre dos personas cuyo pie mida 23.5 y 23.8 cm, siempre es posible encontrar otra cuyo pie mida, digamos 23.6 cm. Este tipo de variable también es aleatoria, pero continua.
En cuanto al tiempo que dura una llamada telefónica, tampoco es una variable discreta, puesto que hay infinitos valores entre dos tiempos t1 y t2 de duración.
Ejercicio 2: lanzamiento simultáneo de dos monedas
Un experimento consiste en lanzar simultáneamente dos monedas idénticas, para el cual se define la variable aleatoria X = {número de caras}. Encontrar:
a) Los valores que toma X.
b) La distribución de probabilidades
Solución a
Los posibles resultados del experimento son los siguientes: ninguna cara (dos sellos), una cara y un sello, un sello y una cara y, por último, dos caras.
Denotando la cara como C y el sello como S, los resultados se resumen así:
Ω = {(S,S); (C,S); (S,C); (C,C)}
Este conjunto se conoce como el espacio muestral.
Por lo tanto, la variable aleatoria X toma los valores: 0 (ninguna cara), 1 (una cara en cualquiera de las dos monedas) y 2 (salió cara en ambas monedas). Dado que los resultados son contables, la variable, además de aleatoria, es discreta:
X = {0,1,2}
Solución b
Cuando se lanza una moneda, si es honesta, la cara o sello tienen idéntica probabilidad de salir, igual a ½. Por eso, si se lanzan dos monedas simultáneamente, dado que los resultados son independientes, debido a que las monedas no se influencian entre sí, la probabilidad de obtener dos caras (o dos cruces) se halla multiplicando las probabilidades de cada suceso.
Si se obtienen dos cruces, significa que no salió ninguna cara:
P (2 cruces = 0 caras) = P (X = 0) = ½ ∙ ½ = ¼
En cambio, la probabilidad de que ocurra la combinación CS o SC es la suma de las dos probabilidades favorables:
P (1 cara) = P (X = 1) = ¼ + ¼ = ½
Por último, la probabilidad de obtener dos caras es:
P (2 caras) = P (X = 2) = ½ ∙ ½ = ¼
Nótese que esta distribución de probabilidad cumple con los requisitos estipulados al comienzo:
La probabilidad de cada evento está comprendida entre 0 y 1.
Al sumar las tres probabilidades se obtiene 1: ¼ + ½ + ¼ = 1
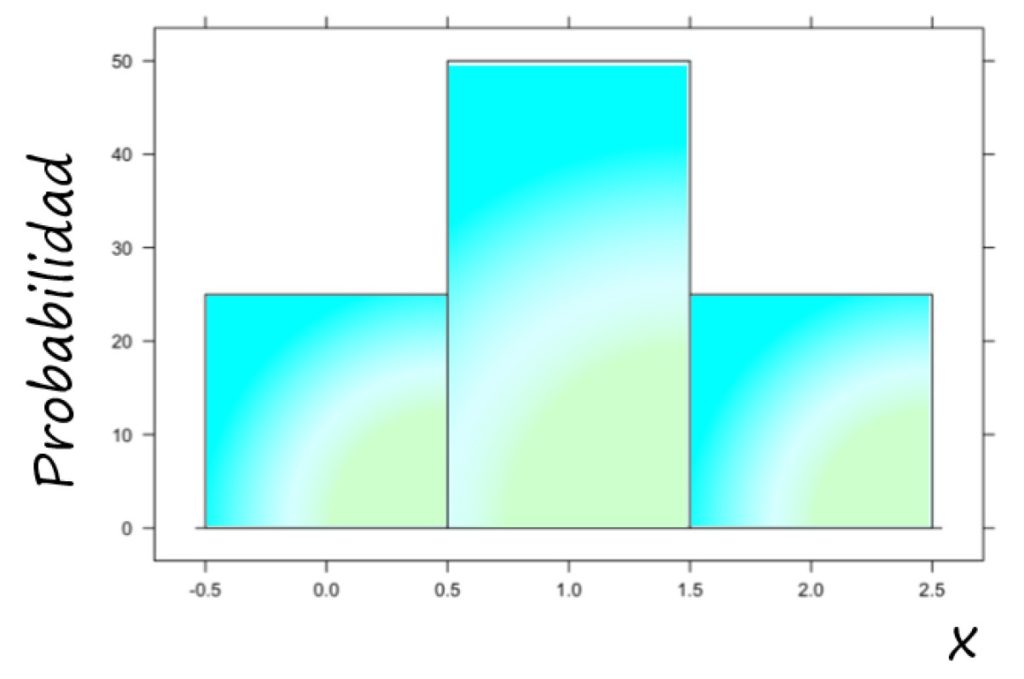
Ejercicio 3: dos lanzamientos de un dado equilibrado
Un experimento consiste en lanzar dos veces seguidas un dado equilibrado. La variable aleatoria que se define es:
X = {número de veces que sale un 1}
a) Listar los resultados posibles del experimento y determinar los valores de la variable aleatoria.
b) Encontrar su distribución de probabilidades.
Solución a
Como es un dado equilibrado, todas las caras tienen la misma probabilidad de salir, y como el dado es un cubo con seis caras, dicha probabilidad es igual a 1/6.
Los resultados posibles del experimento se pueden sintetizar así:
- No se obtiene el 1 ni una sola vez: x1=0
- El 1 sale una sola vez: x2=1
- Ambos lanzamientos resultan 1: x3=2
Por lo tanto, la variable aleatoria X es discreta y tiene tres valores:
X = {0,1,2}
Solución b
En cuanto a la distribución de probabilidades de esta variable, lo primero es notar que el conjunto de todos los posibles resultados consta de 36 pares, los que conforman el espacio muestral:
Ω = {(1,1), (1,2), (1,3) … (1,6); (2,1), (2,2), (2,3) …; (3,1), (3,2), (3,3) …; (4,1), (4,2) … (4,6); (5,1), (5,2) … (5,6); (6,1), (6,2) … (6,6)}
-Ahora se cuentan aquellos pares en los que no se obtiene un 1:
x1 = (X=0) = {(2,2), (2,3) … (2,6); (3,2), (3,3) …; (4,2), (4,3) …; (5,2), (5,3) …; (6,2), (6,3) …}
En total, son 25 pares, en los cuales no sale el 1, por lo tanto, la probabilidad de obtener alguno de estos pares es:
p1 = P (X = 0) = 25/36
-Seguidamente, se cuentan los pares en los que aparece el 1 por una única vez:
x2 = (X=1) = {(1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (3,1), (4,1), (5,1), (6,1)}
Son 10 pares, por lo tanto:
p2 = P (X = 1) = 10/36 = 5/18
-Por último, solo hay un par en el que el 1 sale dos veces: (1,1). Entonces:
p3 = P (X = 2) = 1/36
