Dilatación lineal: qué es, fórmula y coeficientes, ejemplo
La dilatación lineal ocurre cuando un objeto experimenta dilatación a causa de una variación de temperatura, predominantemente en una sola dimensión. Ello se debe a características propias del material o a su forma geométrica.
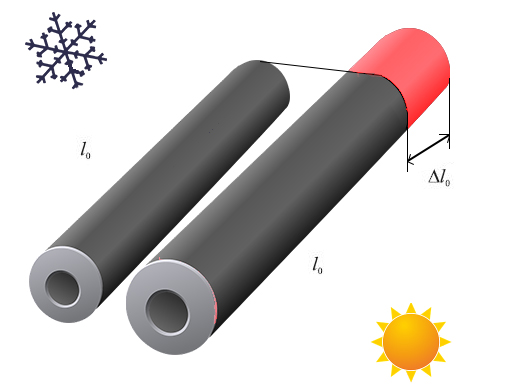
Por ejemplo, en un alambre o en una barra, cuando hay un incremento de temperatura es el largo el que mayor cambio sufre a causa de la dilatación térmica.

Los cables en los que se posan los pájaros de la figura anterior sufren un estiramiento cuando aumenta su temperatura; en cambio, se contraen cuando se enfrían. De igual forma ocurre, por ejemplo, con las barras que forman los rieles de un ferrocarril.
Índice del artículo
- 1 ¿En qué consiste la dilatación lineal?
- 2 Fórmula de la dilatación lineal y su coeficiente
- 3 Ejemplos resueltos de dilatación lineal
- 4 Referencias
En un material sólido, los átomos mantienen sus posiciones relativas más o menos fijas alrededor de un punto de equilibrio. Sin embargo, debido a la agitación térmica, siempre están oscilando en torno al mismo.
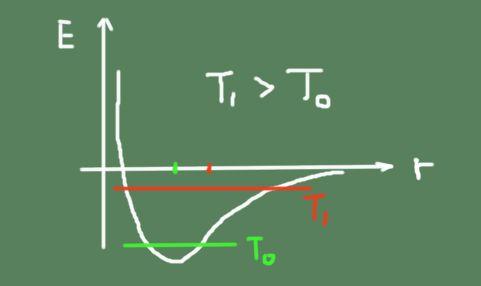
Al aumentar la temperatura, también aumenta la oscilación térmica, haciendo que las posiciones de oscilación media cambien. Esto es debido a que el potencial de enlace no es exactamente parabólico y tiene asimetría alrededor del mínimo.
A continuación se muestra una figura que esboza la energía de enlace químico en función de la distancia interatómica. Se muestra también la energía total de oscilación a dos temperaturas, y cómo se desplaza el centro de oscilación.
Para medir la dilatación lineal, partimos de una longitud de inicial L y una temperatura inicial T, del objeto del que se le quiere medir su dilatación.
Supongamos que dicho objeto es una barra cuya largo es L y las dimensiones de la sección transversal son mucho menores que L.
Primero se somete dicho objeto a una variación de temperatura ΔT, de modo tal que la temperatura final del objeto una vez que se haya establecido el equilibrio térmico con la fuente de calor será T’=T+ ΔT.
Durante este proceso, la longitud del objeto también habrá cambiado a un nuevo valor L’ = L + ΔL, donde ΔL es la variación de la longitud.
Se define el coeficiente de dilatación lineal α como el cociente entre la variación relativa de longitud por unidad de variación de temperatura. La siguiente fórmula define el coeficiente de dilatación lineal α:
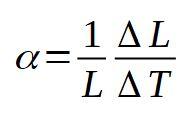
Las dimensiones del coeficiente de dilatación lineal son las del inverso de la temperatura.
A continuación daremos un listado del coeficiente de dilatación lineal para algunos materiales y elementos típicos. El coeficiente está calculado a presión atmosférica normal en base a una temperatura ambiente de 25 °C; y su valor se considera constante en un rango de ΔT de hasta 100 °C.
La unidad del coeficiente de dilatación lineal será (°C)-1.
– Acero: α = 12∙10-6 (°C)-1
– Aluminio: α = 23∙10-6 (°C)-1
– Oro: α = 14∙10-6 (°C)-1
– Cobre: α = 17∙10-6 (°C)-1
– Latón: α = 18∙10-6 (°C)-1
– Hierro: α = 12∙10-6 (°C)-1
– Vidrio: α = (7 a 9)∙10-6 (°C)-1
– Mercurio: α = 60,4∙10-6 (°C)-1
– Cuarzo: α = 0,4∙10-6 (°C)-1
– Diamante: α = 1,2∙10-6 (°C)-1
– Plomo: α = 30∙10-6 (°C)-1
– Madera de roble: α = 54∙10-6 (°C)-1
– PVC: α = 52∙10-6 (°C)-1
– Fibra de carbono: α = -0.8∙10-6 (°C)-1
– Hormigón: α = (8 a 12)∙10-6 (°C)-1
La mayoría de los materiales se estiran con un aumento de temperatura. Sin embargo, algunos materiales especiales como la fibra de carbono se encogen con el aumento de temperatura.
Un cable de cobre está colgado entre dos postes, y su longitud en un día fresco a 20 °C es de 12 m. Calcule el valor de su longitud en un día caluroso a 35 °C.
Solución
Partiendo de la definición del coeficiente de dilatación lineal, y sabiendo que para el cobre este coeficiente vale: α = 17∙10-6 (°C)-1
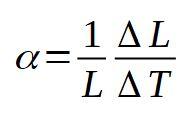
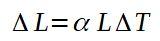
El cable de cobre sufre un aumento de su longitud, pero este es apenas de 3 mm. Es decir, el cable pasa de tener 12,000 m a tener 12,003 m.
En una herrería, una barra de aluminio sale del horno a 800 grados centígrados, midiendo una longitud de 10,00 m. Una vez que se enfría a la temperatura ambiente de 18 grados centígrados, determine el largo que tendrá la barra.
Solución
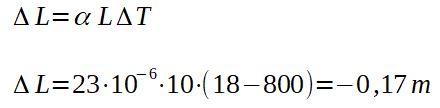
Es decir que la barra, una vez fría, tendrá una longitud total de:
9,83 m.
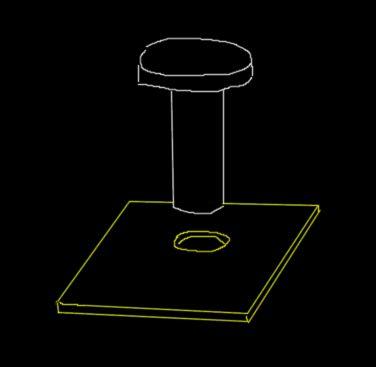
Un remache de acero tiene un diámetro de 0.915 cm. Sobre una placa de aluminio se hace un hueco de 0,910 cm. Esto son los diámetros iniciales cuando la temperatura ambiente es de 18 °C.
¿A qué temperatura mínima debe calentarse la placa para que el remache pase por el agujero? El objetivo de esto es que cuando la plancha vuelva a la temperatura ambiente, el remache quede ajustado en la placa.
Solución
Aunque la placa es una superficie, estamos interesados en la dilatación del diámetro del agujero, que es una cantidad unidimensional.
Llamemos D0 al diámetro original de la placa de aluminio, y D al que tendrá una vez calentada.
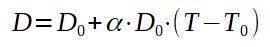
Despejando la temperatura final T, se tiene:
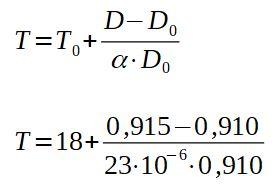
El resultado de las operaciones anteriores es 257 °C, que es la mínima temperatura a la que ha de calentarse la placa para que el remache pase por el agujero.
El remache y la placa del ejercicio anterior se colocan juntos en un horno. Determine a qué temperatura mínima debe estar el horno para que el remache de acero pase por el agujero de la placa de aluminio.
Solución
En este caso, tanto el remache como el agujero se van a dilatar. Pero el coeficiente de dilatación del acero es α = 12∙10-6 (°C)-1, mientras que el del aluminio es α = 23∙10-6 (°C)-1 .
Buscamos entonces una temperatura final T tal que ambos diámetros coincidan.
Si llamamos 1 al remache y 2 a la placa de aluminio, buscamos una temperatura final T tal que D1 = D2.
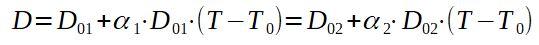
Si despejamos la temperatura final T, nos queda:
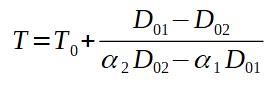
A continuación colocamos los valores correspondientes.
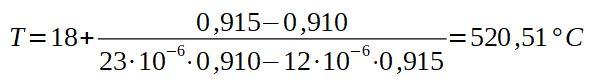
La conclusión es que el horno debe estar como mínimo a 520,5 °C para que el remache pase por el agujero de la placa de aluminio.
- Giancoli, D. 2006. Physics: Principles with Applications. Sixth Edition. Prentice Hall. 238–249.
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mac Graw Hill. 422-527.
