Permutaciones circulares: demostración, ejemplos, ejercicios resueltos
Las permutaciones circulares son diferentes tipos de agrupaciones de todos los elementos de un conjunto, cuando estos han de ordenarse en círculos. En este tipo de permutación importa el orden y no se repiten los elementos.
Por ejemplo, suponga que se desea conocer el número de arreglos distintos de los dígitos del uno al cuatro, ubicando cada número en uno de los vértices de un rombo. Estos serían 6 arreglos en total:

No se debe confundir que el número uno esté en la posición superior del rombo en todos los casos como una posición fija. Las permutaciones circulares no cambian por el giro del arreglo. Los siguientes son una sola o la misma permutación:
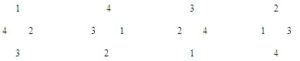
Índice del artículo
En el ejemplo de los arreglos circulares diferentes de 4 dígitos ubicados en los vértices de un rombo, el número de arreglos (6) se puede averiguar así:
1- Se toma cualquiera de los cuatro dígitos como punto de partida en cualquiera de los vértices y se avanza al vértice siguiente. (es indiferente si se gira en el sentido del reloj o en sentido contrario al reloj)
2- Quedan 3 opciones para seleccionar el segundo vértice, luego quedan 2 opciones para seleccionar el tercer vértice y, por supuesto, solo queda una opción de selección para el cuarto vértice.
3- Así pues, el número de permutaciones circulares, denotado por (4 – 1)P(4 – 1), se obtiene por el producto de las opciones de selección en cada posición:
(4 – 1)P(4 – 1) = 3*2*1 = 6 arreglos circulares distintos de 4 dígitos.
De manera general, el número de permutaciones circulares que se pueden conseguir con todos los n elementos de un conjunto es:
(n – 1)P(n – 1) = (n – 1)! = (n – 1)(n – 2)…(2)(1)
Reseñarse que (n – 1)! es conocida como n factorial y abrevia el producto de todos los números desde el número (n – 1) hasta el número uno, ambos incluidos.
¿Cuántas formas distintas tienen 6 personas de sentarse a una mesa circular?
Se quiere hallar el número de formas distintas en que 6 personas pueden sentarse alrededor de una mesa redonda.
N° de formas de sentarse = (6 – 1)P(6 – 1) = ( 6 – 1)!
N° de formas de sentarse = 5*4*3*2*1 = 120 formas distintas
¿Cuántas formas distintas tienen 5 personas de ubicarse en los vértices de un pentágono?
Se busca el número de formas en que 5 personas pueden ubicarse en cada uno de los vértices de un pentágono.
N° de formas de ubicarse = (5 – 1)P(5 – 1) = (5 – 1)!
N° de formas de ubicarse = 4*3*2*1 = 24 formas distintas
Un joyero adquiere 12 piedras preciosas diferentes para ubicarlas en los puntos de las horas de un reloj que está preparando por encargo de la casa real de un país europeo.
a) ¿Cuántas formas distintas tiene para ordenar las piedras en el reloj?
b) ¿Cuántas formas distintas tiene si la piedra que va a las 12 es única?
c) ¿Cuántas formas distintas si la piedra de las 12 es única y las piedras de los otros tres puntos cardinales, las 3, las 6 y las 9; son tres piedras particulares, que se pueden intercambiar, y el resto de las horas se asignan del resto de las piedras?
Soluciones
a) Se pide el número de maneras de ordenar en la circunferencia del reloj todas las piedras; es decir, el número de arreglos circulares que involucran todas las piedras disponibles.
N° de arreglos en el reloj = (12 – 1)P(12 – 1) = (12 – 1)!
N° de arreglos en el reloj = 11*10*9*8*7*6*5*4*3*2*1
N° de arreglos en el reloj = 39976800 formas distintas
b) Se pregunta cuántas formas distintas de ordenar existen sabiendo que la piedra de la manilla de las 12 es única y fija; es decir, el número de arreglos circulares que involucran las 11 piedras restantes.
N° de arreglos en el reloj = (11 – 1)P(11 – 1) = (11 – 1)!
N° de arreglos en el reloj = 10*9*8*7*6*5*4*3*2*1
N° de arreglos en el reloj = 3628800 formas distintas
c) Por último se busca el número de formas de ordenar todas las piedras excepto la piedra de las 12 que es fija, las piedras de las 3, 6 y 9 que tienen 3 piedras a asignarse entre ellas; es decir, 3! posibilidades de arreglo, y el número de arreglos circulares que involucran las 8 piedras restantes.
N° de arreglos en el reloj = 3!*[(8–1)P(8-1)] = 3!*(8–1)!
N° de arreglos en el reloj = (3*2*1)(8*7*6*5*4*3*2*1)
N° de arreglos en el reloj = 241920 formas distintas
El comité directivo de una empresa consta de 8 miembros y se reúnen en una mesa ovalada.
a) ¿Cuántas formas distintas de ordenamiento alrededor de la mesa tiene el comité?
b) Supóngase que el presidente se sienta en la cabecera de la mesa en cualquier arreglo del comité, ¿Cuántas formas distintas de ordenamiento tiene el resto del comité?
c) Supóngase que a los lados del presidente se sientan el vicepresidente y el secretario en cualquier arreglo del comité, ¿Cuántas formas distintas de ordenamiento tiene el resto del comité?
Soluciones
a) Se quiere hallar el número de formas distintas de ordenar los 12 miembros del comité alrededor de la mesa ovalada.
N° de arreglos del comité = (12 – 1)P(12 – 1) = (12 – 1)!
N° de arreglos del comité = 11*10*9*8*7*6*5*4*3*2*1
N° de arreglos del comité = 39976800 formas distintas
b) Ya que el presidente del comité se ubica en una posición fija, se busca el número de formas de ordenar los 11 miembros restantes del comité alrededor de la mesa ovalada.
N° de arreglos del comité = (11 – 1)P(11 – 1) = (11 – 1)!
N° de arreglos del comité = 10*9*8*7*6*5*4*3*2*1
N° de arreglos del comité = 3628800 formas distintas
c) El presidente se ubica en una posición fija y a los lados se ubican el vicepresidente y el secretario con dos posibilidades de arreglo: vicepresidente a la derecha y secretario a la izquierda o vicepresidente a la izquierda y secretario a la derecha. Luego se quiere hallar el número de formas distintas de ordenar los 9 miembros restantes del comité alrededor de la mesa ovalada y multiplicar por las 2 formas de arreglos que tienen el vicepresidente y el secretario.
N° de arreglos del comité = 2*[(9–1)P(9-1)] = 2*[(9–1)!]
N° de arreglos del comité = 2*(8*7*6*5*4*3*2*1)
N° de arreglos del comité = 80640 formas distintas
- Boada, A. (2017). Uso de la permutación con repetición como enseñanza de experimentos. Revista Vivat Academia. Recuperado de researchgate.net.
- Canavos, G. (1988). Probabilidad y Estadística. Aplicaciones y métodos. McGraw-Hill/Interamericana de México S. A. de C. V.
- Glass, G.; Stanley, J. (1996). Métodos estadísticos no aplicados a las ciencias sociales. Prentice Hall Hispanoamericana S. A.
- Spiegel, M.; Stephens, L. (2008). Estadística. Cuarta ed. McGraw-Hill/Interamericana de México S. A.
- Walpole, R.; Myers, R.; Myers, S.; Ye, Ka. (2007). Probability & Statistics for engineers & scientists. Eighth ed. Pearson Education Internacional Prentice Hall.
- Webster, A. (2000). Estadística aplicada a los negocios y la economía. Tercera ed. McGraw-Hill/Interamericana S. A.
- Wikipedia. (2019). Permutation. Recuperado de en.wikipedia.org.
