Error estándar de estimación: cómo se calcula, ejemplos, ejercicios
El error estándar de estimación mide la desviación en una muestra valor poblacional. Es decir, el error estándar de estimación mide las posibles variaciones de la media muestral con respecto al verdadero valor de la media poblacional.
Por ejemplo, si se desea conocer la edad promedio de la población de un país (media poblacional) se toma un pequeño grupo de habitantes, a los que llamaremos “muestra”. De ella se extrae la edad promedio (media muestral) y se asume que la población tiene esa edad promedio con un error estándar de estimación que varía más o menos.
Habría que reseñar que es importante no confundir la desviación estándar con el error estándar y con el error estándar de estimación:
1- La desviación estándar es una medida de la dispersión de los datos; es decir, es una medida de la variabilidad de la población.
2- El error estándar es una medida de la variabilidad de la muestra, calculada en base a la desviación estándar de la población.
3- El error estándar de estimación es una medida del error que se comete al tomar la media muestral como estimación de la media poblacional.
Índice del artículo
El error estándar de estimación se puede calcular para todas las medidas que se obtienen en las muestras (por ejemplo, error estándar de estimación de la media o error estándar de estimación de la desviación estándar) y mide el error que se comete al estimar la verdadera medida poblacional a partir de su valor muestral
A partir del error estándar de estimación se construye el intervalo de confianza de la medida correspondiente.
La estructura general de una fórmula para el error estándar de estimación es la siguiente:
Error estándar de estimación = ± Coeficiente de confianza * Error estándar
Coeficiente de confianza = valor límite de un estadístico muestral o distribución de muestreo (normal o campana de Gauss, t de Student, entre otras) para un determinado intervalo de probabilidades.
Error estándar = desviación estándar de la población dividida por la raíz cuadrada del tamaño de la muestra.
El coeficiente de confianza indica la cantidad de errores estándar que está dispuesto a sumar y restar a la medida para tener un cierto nivel de confianza en los resultados.
Suponga que está tratando de estimar la proporción de personas en la población que tienen una conducta A, y se desea tener un 95% de confianza en sus resultados.
Se toma una muestra de n personas y se determina la proporción muestral p y su complemento q.
Error estándar de estimación (EEE) = ± Coeficiente de confianza * Error estándar
Coeficiente de confianza = z = 1.96.
Error estándar = la raíz cuadrada de la razón entre el producto de la proporción muestral por su complemento y el tamaño de la muestra n.
A partir del error estándar de estimación se establece el intervalo en el que se espera se encuentre la proporción poblacional o la proporción muestral de otras muestras que se puedan formar de esa población, con un 95% de nivel de confianza:
p – EEE ≤ Proporción poblacional ≤ p + EEE
1- Suponga que está tratando de estimar la proporción de personas en la población que tienen preferencia por una fórmula láctea enriquecida, y se desea tener un 95% de confianza en sus resultados.
Se toma una muestra de 800 personas y se determina que 560 personas en la muestra tiene preferencia por la fórmula láctea enriquecida. Determine un intervalo en el cual se pueda esperar se encuentre la proporción poblacional y la proporción de otras muestras que se puedan tomar de la población, con un 95% de confianza
a) Calculemos la proporción muestral p y su complemento:
p = 560/800 = 0.70
q = 1 – p = 1 – 0.70 = 0.30
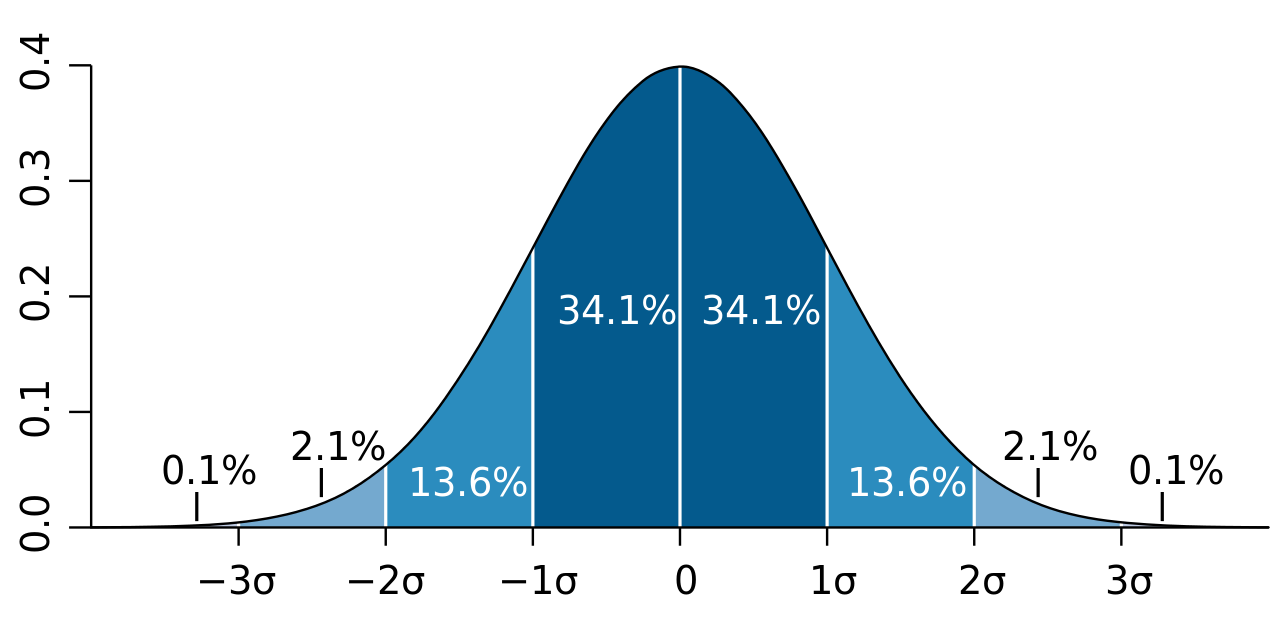
b) Se conoce que la proporción se aproxima a una distribución normal a muestras de tamaño grande (mayores a 30). Entonces, se aplica la llamada regla 68 – 95 – 99.7 y se tiene que:
Coeficiente de confianza = z = 1.96
Error estándar = √(p*q/n)
Error estándar de estimación (EEE) = ± (1.96)*√(0.70)*(0.30)/800) = ± 0.0318
c) A partir del error estándar de estimación se establece el intervalo en el que se espera se encuentre la proporción poblacional con un 95% de nivel de confianza:
0.70 – 0.0318 ≤ Proporción poblacional ≤ 0.70 + 0.0318
0.6682 ≤ Proporción poblacional ≤ 0.7318
Se puede esperar que la proporción de muestra del 70% cambie hasta en 3.18 puntos porcentuales si toma una muestra diferente de 800 individuos o que la proporción real de la población está entre 70 – 3.18 = 66.82% y 70 + 3.18 = 73.18%.
2- Tomaremos de Spiegel y Stephens, 2008, el siguiente caso estudio:
Del total de calificaciones de matemáticas de los alumnos de primer año de una universidad se tomó una muestra aleatoria de 50 calificaciones en la que la media encontrada fue 75 puntos y la desviación estándar, 10 puntos. ¿Cuáles son los límites de confianza de 95% para la estimación de la media de las calificaciones de matemática de la universidad?
a) Calculemos el error estándar de estimación:
Coeficiente de confianza del 95% = z = 1.96
Error estándar = s/√n
Error estándar de estimación (EEE) = ± (1.96)*(10√50) = ± 2.7718
b) A partir del error estándar de estimación se establece el intervalo en el que se espera se encuentre la media poblacional o la media de otra muestra de tamaño 50, con un 95% de nivel de confianza:
50 – 2.7718 ≤ Promedio poblacional ≤ 50 + 2.7718
47.2282 ≤ Promedio poblacional ≤ 52.7718
c) Se puede esperar que la media de la muestra cambie hasta en 2.7718 puntos si se toma una muestra diferente de 50 calificaciones o que la media real de las calificaciones de matemática de la población de la universidad está entre 47.2282 puntos y 52.7718 puntos.
- Abraira, V. (2002). Desviación estándar y error estándar. Revista Semergen. Recuperado de web.archive.org.
- Rumsey, D. (2007). Intermediate statistics for dummies. Wiley Publishing, Inc.
- Salinas, H. (2010). Estadística y probabilidades. Recuperado de mat.uda.cl.
- Sokal, R.; Rohlf, F. (2000). Biometry. The principles and practice of statistics in biological research. Third ed. Blume Ediciones.
- Spiegel, M.; Stephens, L. (2008). Estadística. Cuarta ed. McGraw-Hill/Interamericana de México S. A.
- Wikipedia. (2019). 68-95-99.7 rule. Recuperado de en.wikipedia.org.
- Wikipedia. (2019). Standard error. Recuperado de en.wikipedia.org.
