Funciones trascendentes: tipos, definición, propiedades, ejemplos

Las funciones trascendentes elementales son las exponenciales, las logarítmicas, las trigonométricas, las funciones trigonométricas inversas, las hiperbólicas y las hiperbólicas inversas. Es decir, son aquellas que no pueden ser expresadas mediante un polinomio, un cociente de polinomios o raíces de polinomios. 

Las funciones trascendentes no-elementales, también se le conocen como funciones especiales y entre ellas puede nombrarse la función error. Las funciones algebraicas (polinomios, cocientes de polinomios y raíces de polinomios) junto a las funciones trascendentes elementales constituyen lo que en matemáticas se conoce como funciones elementales.

Se consideran funciones trascendentes también las que resultan de operaciones entre funciones trascendentes o entre funciones trascendentes y algebraicas. Estas operaciones son: la suma y diferencia de funciones, producto y cociente de funciones, así como la composición de dos o más funciones.

Índice del artículo

• 1 Definición y propiedades
  • 1.1 Función exponencial
  • 1.2 Propiedades de la función exponencial
  • 1.3 Función logarítmica
  • 1.4 Propiedades de la función logaritmo
  • 1.5 Funciones seno, coseno y tangente
• 2 Derivadas e integrales
  • 2.1 Derivada de la función exponencial
  • 2.2 Integral de la función exponencial
  • 2.3 Tabla de derivadas e integrales de las funciones trascendentes
• 3 Ejemplos
  • 3.1 Ejemplo 1
  • 3.2 Ejemplo 2
• 4 Referencias

Definición y propiedades

Función exponencial

Es una función real de variable independiente real de la forma:

f(x) = a^x = a^x

donde a es un número real positivo (a>0) fijo denominado la base. El circunflejo o el superíndice se usan para denotar la operación de potenciación.

Pongamos por caso que a = 2 entonces la función queda así:

f(x) = 2^x = 2^x

La cual se evaluará para varios valores de la variable independiente x:

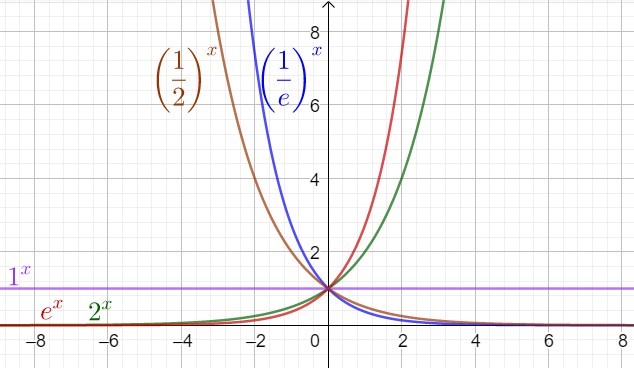
A continuación se muestra un gráfico donde se representa la función exponencial para varios valores de la base, incluyendo la base e (número de Neper e ≃ 2.72). La base e es tan importante que, por lo general, cuando se habla de función exponencial se piensa en e^x, que también se denota exp(x).

Propiedades de la función exponencial

De la figura 1 puede observarse que el dominio de las funciones exponenciales son los números reales (Dom f = R) y el rango o recorrido son los reales positivos (Ran f = R⁺). 

Por otra parte, independientemente del valor de la base a, todas las funciones exponenciales pasan por el punto (0, 1) y por el punto (1, a). 

Cuando la base a > 1, entonces la función es creciente y cuando 0 a 1 la función es decreciente. 

Las curvas de y=a^x y de y= (1/a)^x  son simétricas respecto al eje Y. 

Con excepción del caso a=1, la función exponencial es inyectiva, es decir a cada valor de la imagen corresponde uno y solo un valor de partida.

Función logarítmica

Es una función real de variable independiente real basada en la definición del logaritmo de un número. El logaritmo en base a de un número x, es el número y al cual debe elevarse la base para obtener el argumento x:

log_a(x) = y  ⇔ a^y = x

Es decir, que la función logaritmo en base a es la función inversa a la función exponencial en base a.

Por ejemplo:

log₂1 = 0, ya que 2^0 =1

Otro caso, log₂4 = 2, porque 2^2 =4

El logaritmo de raíz de 2 es log₂√2 = ½ , debido a que 2^½  =√2

log₂ ¼ = -2, en vista que 2^(-2) = ¼ 

A continuación se muestra un gráfico de la función logaritmo en diversas bases.

Propiedades de la función logaritmo

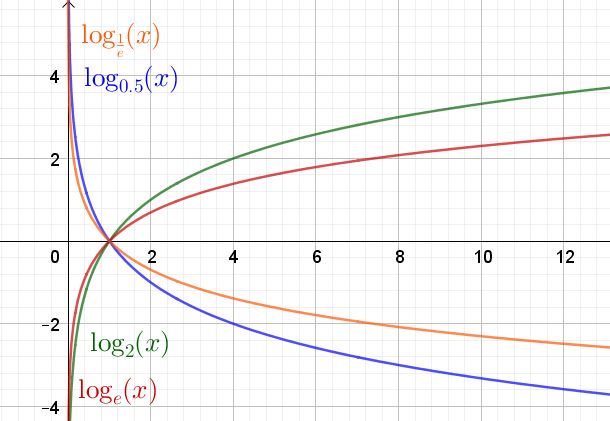
El dominio de la función logaritmo y(x) = loga(x)  son los números reales positivos R+. El rango o recorrido son los números reales R.

Independientemente de la base, la función logaritmo siempre pasa por el punto (1,0) y el punto (a, 1) pertenece al gráfico de dicha función.

En el caso que la base a sea mayor que la unidad (a > 1) la función logaritmo es creciente. Pero si (0 a 1) entonces es una función decreciente.

Funciones seno, coseno y tangente

La función seno asigna un número real y a cada valor x, donde x representa la medida de un ángulo en radianes. Para obtener el valor del Sen(x) de un ángulo, se representa el ángulo en el círculo unitario y la proyección de dicho ángulo sobre el eje vertical es el seno correspondiente a ese ángulo.

A continuación se muestra (en la figura 3) el círculo trigonométrico y el seno para varios valores angulares X1, X2, X3 y X4.

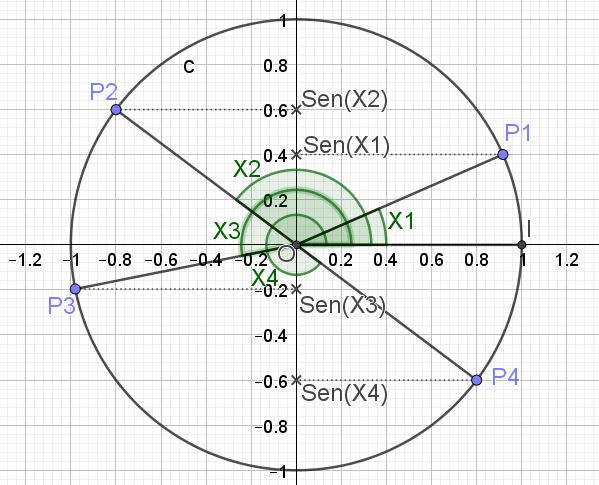
Definida en esta forma el máximo valor que puede tener la función Sen(x) es 1, el cual ocurre cuando x= π/2 + 2π n, siendo n un número entero (0,±1, ±2, ). El mínimo valor que puede tomar la función Sen(x) ocurre cuando x = 3π/2 + 2π n. 

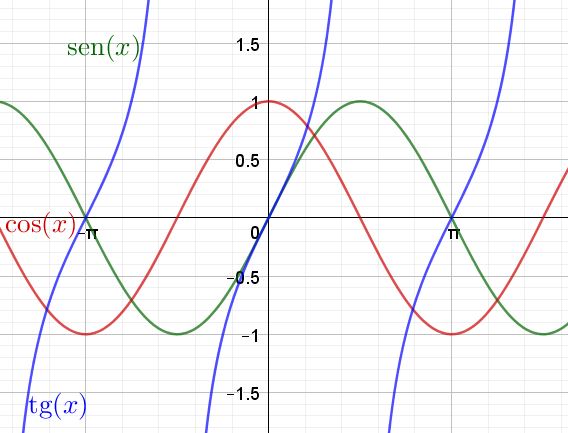
La función coseno y = Cos(x) se define en forma similar, pero la proyección de las posiciones angulares P1, P2, etc se realiza sobre el eje horizontal del círculo trigonométrico.

Por otra parte, la función y = Tan(x) es el cociente entre la función seno y la función coseno.

Seguidamente se muestra un gráfico de las funciones trascendentes Sen(x), Cos(x) y Tan(x)

Derivadas e integrales

Derivada de la función exponencial

La derivada y’ de la función exponencial y = a^x es la función a^x multiplicada por el logaritmo neperiano de la base a:

y’ = (a^x)’ = a^x ln a

En el caso particular de la base e, la derivada de la función exponencial es la propia función exponencial.

Integral de la función exponencial

La integral indefinida de a^x es la propia función dividida entre el logaritmo neperiano de la base. 

En el caso particular de la base e, la integral de la función exponencial es la propia función exponencial.

Tabla de derivadas e integrales de las funciones trascendentes

A continuación se muestra una tabla resumen de las principales funciones trascendentes, sus derivadas e integrales indefinidas (antiderivadas):

Ejemplos

Ejemplo 1

Encontrar la función resultante de la composición de la función f(x) = x^3 con la función g(x) = cos(x):

(f o g) (x) = f(g(x)) = cos³(x)

Su derivada y su integral indefinida es:

Ejemplo 2

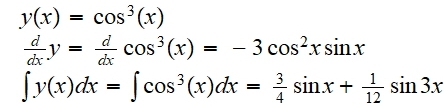
Hallar la composición de la función g con la función f, siendo g y f las funciones definidas en el ejemplo anterior:

(g o f) (x) = g(f(x)) = cos(x³)

Debe notarse que la composición de funciones no es una operación conmutativa.

La derivada y la integral indefinida para esta función son respectivamente:

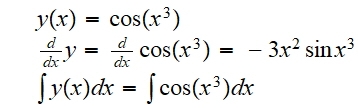
La integral se dejó indicada debido a que no es posible escribir el resultado como combinación de funciones elementales en forma exacta.

Referencias

1. Calculus of a Single Variable. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 nov. 2008
2. The Implicit Function Theorem: History, Theory, and Applications. Steven G. Krantz, Harold R. Parks. Springer Science & Business Media, 9 nov. 2012
3. Multivariable Analysis. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 dic. 2010
4. System Dynamics: Modeling, Simulation, and Control of Mechatronic Systems. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 mar. 2012
5. Calculus: Mathematics and Modeling. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 ene. 1999
6. wikipedia. Función trascendente. Recuperado de: es.wikipedia.com