Choques inelásticos: en una dimensión y ejemplos
Los choques inelásticos o colisiones inelásticas son una breve e intensa interacción entre dos objetos en la cual la cantidad de movimiento se conserva, pero no así la energía cinética, de la cual un porcentaje es transformado en algún otro tipo de energía.
Los choques o colisiones son frecuentes en la naturaleza. Las partículas subatómicas colisionan a altísimas velocidades, mientras que muchos deportes y juegos consisten en continuas colisiones. Hasta las galaxias son capaces de colisionar.

En realidad la cantidad de movimiento se conserva en cualquier tipo de colisión, siempre y cuando las partículas que colisionan conformen un sistema aislado. Así que en este sentido no hay problema. Ahora bien, los objetos poseen energía cinética asociada al movimiento que tienen. ¿Qué puede suceder con esa energía al momento de chocar?
Las fuerzas internas que tienen lugar durante el choque entre los objetos son intensas. Cuando se afirma que la energía cinética no se conserva, significa que se transforma en otros tipos de energía: por ejemplo, en energía sonora (una colisión aparatosa tiene un sonido distintivo).
Más posibilidades de uso para la energía cinética: calor por fricción, y desde luego la inevitable deformación que sufren los objetos al colisionar, como las carrocerías de los coches de la figura de arriba.
Índice del artículo
- 1 Ejemplos de colisiones inelásticas
- 2 Colisiones perfectamente inelásticas en una dimensión
- 3 Coeficiente de restitución
- 4 ¿Cómo determinar el coeficiente de restitución?
- 5 Ejemplos resueltos
- 6 Referencias
– Dos masas de plastilina que chocan y quedan juntas, moviéndose como una sola pieza después del choque.
– Una pelota de goma que rebota contra una pared o un piso. La pelota se deforma al impactar la superficie.
No toda la energía cinética se transforma en otros tipos de energía, salvo en contadas excepciones. Los objetos pueden quedarse con cierta cantidad de esta energía. Más adelante veremos cómo calcular el porcentaje.
Cuando las piezas que chocan quedan unidas, la colisión se denomina perfectamente inelástica, y ambas suelen terminar moviéndose juntas.
La colisión de la figura muestra dos objetos de distintas masas m1 y m2, moviéndose uno hacia el otro con velocidades vi1 y vi2 respectivamente. Todo ocurre sobre la horizontal, es decir, se trata de una colisión en una dimensión, las más sencillas de estudiar.
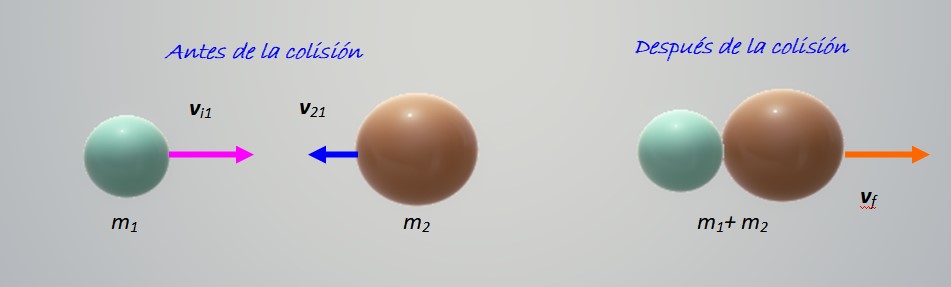
Los objetos colisionan y luego quedan unidos moviéndose hacia la derecha. Es una colisión perfectamente inelástica, así que basta con que conservemos la cantidad de movimiento:
Po = Pf
La cantidad de movimiento es un vector cuyas unidades en SI son N.s. En la situación descrita, puede prescindirse de la notación vectorial al tratarse de colisiones en una dimensión:
mvo = mvf
La cantidad de movimiento del sistema es la suma vectorial de la cantidad de movimiento de cada partícula.
m1 vi1 + m2 vi2 = (m1 + m2)vf
La velocidad final viene dada por:
vf = (m1 vi1 + m2 vi2)/ ( m1 + m2)
Hay una cantidad que puede indicar cómo de elástica es una colisión. Se trata del coeficiente de restitución, el cual se define como el cociente negativo entre la velocidad relativa de las partículas después del choque y la velocidad relativa antes del choque.
Sean u1 y u2 las velocidades respectivas de las partículas inicialmente. Y sean v1 y v2 las velocidades finales respectivas. Matemáticamente el coeficiente de restitución se puede expresar así:
– Si ε = 0 equivale a afirmar que v2 = v1. Significa que las velocidades finales son las mismas y el choque es inelástico, como el que se describió en el apartado anterior.
– Cuando ε = 1 significa que las velocidades relativas tanto antes como después del choque no cambian, en este caso el choque es elástico.
– Y si 0 ε 1 parte de la energía cinética de la colisión se transforma en alguna otra de las energías mencionadas anteriormente.
El coeficiente de restitución depende de la clase de materiales que intervengan en la colisión. Una prueba muy interesante para determinar cómo de elástico es un material para fabricar balones consiste en dejar caer el balón sobre una superficie fija y medir la altura de rebote.
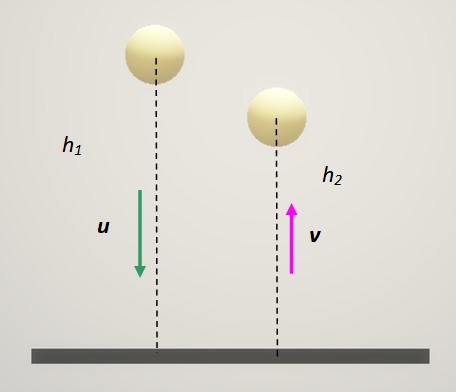
En este caso la placa fija siempre tiene velocidad 0. Si a esta se le asigna el índice 1 y al balón el índice 2 queda:
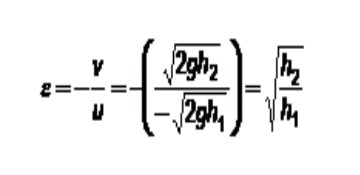
Al comienzo se ha sugerido que toda la energía cinética puede transformarse pasando a otros tipos de energía. Después de todo, la energía no se destruye. ¿Es posible que objetos que venían con movimiento colisionen y se unan formando un solo objeto que súbitamente quede en reposo? Esto no es tan sencillo de imaginar.
Sin embargo, imaginemos que sucede al revés, como en una película vista en retroceso. Entonces el objeto estaba en reposo inicialmente y luego explota fragmentándose en varias partes. Esta situación es perfectamente posible: se trata de una explosión.
De manera que una explosión puede pensarse como una colisión perfectamente inelástica vista hacia atrás en el tiempo. La cantidad de movimiento igualmente se conserva, pudiendo afirmarse que:
Po = Pf
Se conoce a partir de mediciones que el coeficiente de restitución del acero es 0.90. Se deja caer una bola de acero desde 7 m de altura sobre una placa fija. Calcule:
a) Hasta que altura rebotará.
b) Cuánto tiempo tarda entre el primer contacto con la superficie y el segundo.
Solución
a) Se utiliza la ecuación que se dedujo anteriormente en el apartado acerca de la determinación del coeficiente de restitución:
Se despeja la altura h2:
0.902 . 7 m = 5.67 m
b) Para que suba los 5.67 metros se requiere una velocidad dada por:
t max = vo/ g = (10.54 / 9.8 s)= 1.08 s.
El tiempo que tarda en regresar es el mismo, por lo tanto el tiempo total para subir los 5.67 metros y regresar al punto de partida es el doble del tiempo máximo:
tvuelo = 2.15 s.
La figura muestra un bloque de madera de masa M colgando en reposo de hilos de longitud l a modo de péndulo. Esto se llama péndulo balístico y sirve para medir la velocidad v de entrada una bala de masa m. Cuanto mayor sea la velocidad con que la bala impacte al bloque, a mayor altura h este se levantará.
La bala de la imagen queda incrustada en el bloque, por lo tanto es un choque totalmente inelástico.
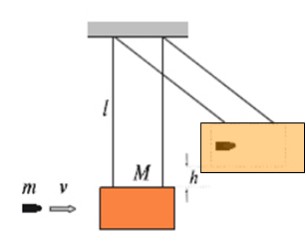
Suponga que una bala de 9.72 g impacta contra el bloque de masa 4.60 kg, luego el conjunto se eleva a 16.8 cm de la posición de equilibrio. ¿Cuál es la velocidad v de la bala?
Solución
Durante la colisión se conserva la cantidad de movimiento y ufes la velocidad del conjunto, una vez que la bala se ha incrustado en el bloque:
Po = Pf
El bloque se encuentra en reposo inicialmente, mientras que la bala se dirige al blanco con velocidad v:
m.v + M.0 = (m + M) uf
No se conoce uftodavía, pero después de la colisión la energía mecánica se conserva, siendo esta la suma de la energía potencial gravitatoria U y la energía cinética K:
Energía mecánica inicial = Energía mecánica final
Emo = Emf
Uo + Ko = Uf + Kf
La energía potencial gravitatoria depende de la altura a la que llegue el conjunto. Para la posición de equilibrio la altura inicial es la que se toma como nivel referencia, por lo tanto:
Uo = 0
Gracias a la bala, el conjunto tiene energía cinética Ko, la cual se convierte en energía potencial gravitatoria cuando el conjunto alcanza su máxima altura h. La energía cinética viene dada por:
K = ½ mv2
Inicialmente la energía cinética es:
Ko =(1/2) (M+m) uf2
Recuérdese que ya la bala y el bloque forman un objeto único de masa M+ m. La energía potencial gravitatoria cuando han llegado a su altura máxima es:
Uf = (m + M)gh
Por lo tanto:
Ko = Uf
(1/2) (M+m) uf2 = (m + M)gh
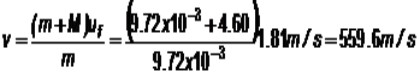
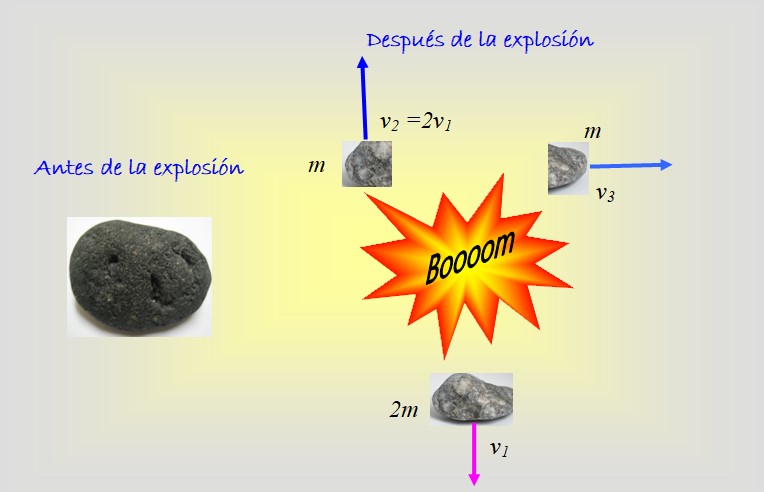
El objeto de la figura explota en tres fragmentos: dos de igual masa m y uno más grande de masa 2m. En la figura se señalan las velocidades de cada fragmento después de la explosión. ¿Cuál era la velocidad inicial del objeto?
Solución
En este problema se requiere el uso de dos coordenadas: x e y, porque dos de los fragmentos tienen velocidades verticales, mientras que el restante tiene velocidad horizontal.
La masa total del objeto es la suma de la masa de todos los fragmentos:
M = m + m + 2m = 4m
La cantidad de movimiento se conserva tanto en el eje x como en el eje y, se plantea por separado:
- 4m. ux= m v3
- 4m. uy = m. 2v1 – 2m. v1
Nótese que el fragmento grande se mueve hacia abajo con velocidad v1, para señalar este hecho se le ha colocado un signo negativo.
De la segunda ecuación se desprende inmediatamente que uy = 0, y de la primera se despeja ux de inmediato:
- Giancoli, D. 2006. Physics: Principles with Applications. 6th. Ed Prentice Hall. 175-181
- Rex, A. 2011. Fundamentos de Física. Pearson. 135-155.
- Serway, R., Vulle, C. 2011. Fundamentos de Física. 9na Cengage Learning. 172 -182
- Tipler, P. (2006) Física para la Ciencia y la Tecnología. 5ta Ed. Volumen 1. Editorial Reverté. 217-238
- Tippens, P. 2011. Física: Conceptos y Aplicaciones. 7ma Edición. MacGraw Hill. 185 -195
