Frecuencia acumulada: fórmula, cálculo, distribución, ejemplos

La frecuencia acumulada es la suma de las frecuencias absolutas f, desde la menor hasta la que corresponde a un determinado valor de la variable. A su vez la frecuencia absoluta es la cantidad de veces que aparece una observación en el conjunto de datos.

Evidentemente, la variable de estudio debe ser ordenable. Y como la frecuencia acumulada se obtiene sumando las frecuencias absolutas, resulta que la frecuencia acumulada hasta el último dato, debe coincidir con el total de ellos. De lo contrario hay un error en los cálculos.

Por lo general, la frecuencia acumulada se denota como F_i (o a veces n_i), para distinguirla de la frecuencia absoluta f_i y es importante añadir una columna para ella en la tabla con la que se organizan los datos, conocida como tabla de frecuencias.

De esta forma se facilita, entre otras cosas, llevar la cuenta de cuántos datos se contaron hasta determinada observación.

A F_i se la conoce también como frecuencia acumulada absoluta. Si se divide entre el total de datos, se tiene la frecuencia acumulada relativa, cuya suma final debe ser igual a 1.

Índice del artículo

• 1 Fórmulas
  • 1.1 Otras frecuencias acumuladas
• 2 ¿Cómo sacar la frecuencia acumulada?
  • 2.1 Cómo llenar la tabla de frecuencia
  • 2.2 Tabla de frecuencia
• 3 Distribución de frecuencias acumuladas
• 4 Ejemplo
• 5 Ejercicio propuesto
  • 5.1 Respuesta
• 6 Referencias

Fórmulas

La frecuencia acumulada de un determinado valor de la variable X_i  es la suma de las frecuencias absolutas f de todos los valores menores o iguales a él:

F_i  = f₁ + f₂ + f₃  +… f_i

Al sumar todas las frecuencias absolutas se obtiene el número total de datos N, es decir:

F₁ + F₂ + F₃ + …. + F_n = N

La operación anterior se escribe de manera resumida mediante el símbolo de sumatoria ∑:

∑ F_i = N

Otras frecuencias acumuladas

También se pueden acumular las siguientes frecuencias:

-Frecuencia relativa: se obtiene dividiendo la frecuencia absoluta f_i entre el total de datos N:

f_r = f_i / N

Si se suman las frecuencias relativas desde la menor hasta la que corresponde a una cierta observación, se tiene la frecuencia relativa acumulada. El último valor debe ser igual a 1.

-Frecuencia relativa acumulada porcentual: se multiplica la frecuencia relativa acumulada por 100%.

f_% = (f_i / N) x 100%

Estas frecuencias son útiles para describir el comportamiento de los datos, por ejemplo al  hallar las medidas de tendencia central.

¿Cómo sacar la frecuencia acumulada?

Para sacar la frecuencia acumulada es preciso ordenar los datos y organizarlos en una tabla de frecuencias. El procedimiento se ilustra en la siguiente situación práctica:

-En una tienda en línea que vende teléfonos celulares, el registro de ventas de cierta marca del mes de marzo arrojó, los siguientes valores por día:

1; 2; 1; 3; 0; 1; 0; 2; 4; 2; 1; 0; 3; 3; 0; 1; 2; 4; 1; 2; 3; 2; 3; 1; 2; 4; 2; 1; 5; 5; 3

La variable es el número de teléfonos vendidos al día y es cuantitativa. Los datos así presentados no son tan fáciles de interpretar, por ejemplo los dueños de la tienda podrían estar interesados en saber si existe alguna tendencia, tal como días de la semana en que las ventas de esa marca son mayores.

Información como esta y más, se puede obtener presentando los datos de manera ordenada y especificando las frecuencias.

Cómo llenar la tabla de frecuencia

Para calcular la frecuencia acumulada primero se ordenan los datos:

 0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5

Luego se construye una tabla con la siguiente información:

-La primera columna a la izquierda con la cantidad de teléfonos vendidos, entre 0 y 5 y en orden creciente.

-Segunda columna: frecuencia absoluta, que es la cantidad de días que se vendieron 0 teléfonos, 1 teléfono, 2 teléfonos y así sucesivamente.

-Tercera columna: la frecuencia acumulada, consistente en la suma de la frecuencia anterior más la frecuencia del dato a considerar.

Esta columna comienza con el primer dato de la columna de la frecuencia absoluta, en este caso es 0. Para el siguiente valor, se suma este con el anterior. Se prosigue así hasta llegar al último dato de la frecuencia acumulada, el cual debe coincidir con el total de datos.

Tabla de frecuencia

En la siguiente tabla se muestra la variable “cantidad de teléfonos vendidos en un día”, su frecuencia absoluta y el cálculo detallado de su frecuencia acumulada.

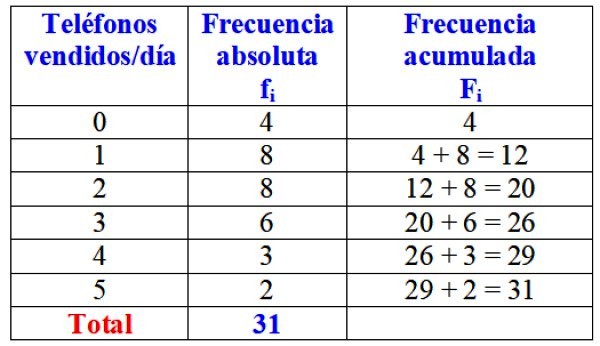
En un primer vistazo, se podría afirmar que de la marca en cuestión, se venden casi siempre uno o dos teléfonos al día, ya que la mayor frecuencia absoluta es de 8 días, que corresponde a estos valores de la variable. Solo durante 4 días del mes no vendieron ni un solo teléfono.

Como se advierte, es más sencillo examinar la tabla que los datos sueltos recogidos originalmente.

Distribución de frecuencias acumuladas

Una distribución de frecuencias acumuladas es una tabla donde se disponen las frecuencias absolutas, las frecuencias acumuladas, las frecuencias relativas acumuladas y las frecuencias porcentuales acumuladas.

Si bien se advierte la ventaja de organizar los datos en una tabla como la anterior, si el número de datos es muy grande es posible que no baste con organizarlos como se mostró arriba, porque si aparecen muchas frecuencias, igual se torna difícil de interpretar.

El problema se puede subsanar construyendo una distribución de frecuencias por intervalos, un procedimiento útil cuando la variable toma un gran número de valores o si es una variable continua.

Aquí los valores se agrupan en intervalos de igual amplitud, llamados clase. Las clases se caracterizan por tener:

-Límite de clase: son los valores extremos de cada intervalo, hay dos, el límite superior y el límite inferior. Por lo general el límite superior no pertenece al intervalo sino al inmediato siguiente, mientras que el límite inferior sí pertenece.

-Marca de clase: es el punto medio de cada intervalo, y se toma como el valor representativo de él.

-Ancho de clase: se calcula restando el valor del dato mayor y el menor (rango) y dividiendo entre el número de clases:

Ancho de clase = Rango / Número de clases

Seguidamente se detalla la elaboración de la distribución de frecuencias.

Ejemplo

Este conjunto de datos corresponde a 40 calificaciones de un examen de Matemáticas, en la escala del 0 al 10:

0; 0;0; 1; 1; 1; 1; 2; 2; 2; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9;10; 10.

Se puede elaborar una distribución de frecuencias con una cierta cantidad de clases, por ejemplo 5 clases. Se debe tener presente que al usar muchas clases, los datos tampoco resultan fáciles de interpretar y se pierde el sentido de llevar a cabo la agrupación.

Y si por el contrario se agrupan en muy pocas, entonces la información se diluye y parte de ella se pierde. Todo depende de la cantidad de datos que se tengan.

En este ejemplo es buena idea disponer de dos puntuaciones en cada intervalo, ya que hay 10 puntuaciones y se van a crear 5 clases. El rango es la resta entre la calificación mayor y la menor, siendo el ancho de clase:

Ancho de clase = (10-0)/5=2

Los intervalos son cerrados por la izquierda y abiertos por la derecha (excepto el último), lo que se simboliza con corchetes y paréntesis respectivamente. Todos tienen el mismo ancho, pero no es obligatorio aunque sí lo más frecuente.

Cada intervalo contiene cierta cantidad de elementos o frecuencia absoluta, y en la columna siguiente está la frecuencia acumulada, en la cual se va llevando la suma. En la tabla también se muestran la frecuencia relativa f_r  (frecuencia absoluta entre el número total de datos) y la frecuencia relativa porcentual f_r ×100%.

Ejercicio propuesto

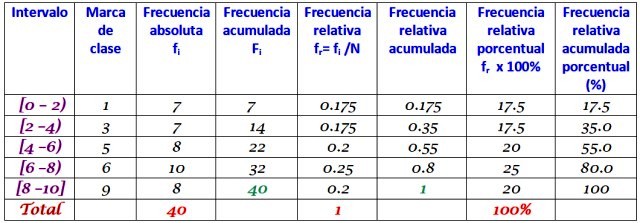
Una empresa hizo llamadas diarias a sus clientes durante los dos primeros meses del año. Los datos son los siguientes:

6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 18, 20, 24, 12, 7, 10, 11, 13, 9, 12, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 16, 9, 6, 10, 12, 20, 13, 17, 14, 26, 7, 12, 24, 7

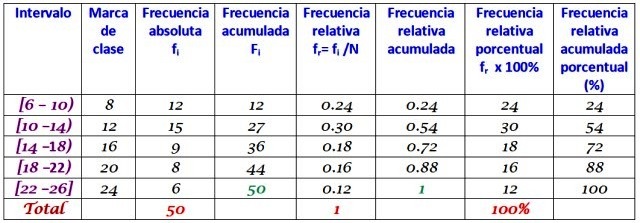
Agrupar en 5 clases y construir la tabla con la distribución de frecuencias.

Respuesta

El ancho de clase es:

(26-6)/5 = 4

Intente resolverlo antes de ver la respuesta.

Referencias

1. Berenson, M. 1985. Estadística para administración y economía. Interamericana S.A.
2. Devore, J. 2012. Probability and Statistics for Engineering and Science. 8th. Edition. Cengage.
3. Levin, R. 1988. Estadística para Administradores. 2da. Edición. Prentice Hall.
4. Probabilidad y Estadística. Anchura de intervalo de clase. Recuperado de: pedroprobabilidadyestadistica.blogspot.com.
5. Spiegel, M. 2009. Estadística. Serie Schaum. 4 ta. Edición. McGraw Hill.
6. Walpole, R. 2007. Probabilidad y Estadística para Ingeniería y Ciencias. Pearson.