Identidades trigonométricas (ejemplos y ejercicios)
Las identidades trigonométricas son relaciones entre razones trigonométricas, las cuales son ciertas para cualquier valor de la variable. Por ejemplo:
tan θ = sen θ /cos θ
Es una identidad trigonométrica que relaciona tres razones del ángulo θ, la tangente, el seno y el coseno de dicho ángulo.

Esta identidad es cierta para todo valor, excepto aquellos que hacen 0 el denominador. El cos θ es 0 para θ = ± π/2, ± 3π/2, ± 5π/2 … Otro ejemplo de identidad trigonométrica es:
sen x . sec x . ctg x = 1
Índice del artículo
Hay dos formas básicas de demostrar que una identidad trigonométrica es cierta:
1- Transformando uno de los miembros de la igualdad en el otro, mediante manipulaciones algebraicas convenientes.
2- Desarrollar ambos miembros de la igualdad por separado, hasta que las respectivas expresiones finales de cada uno sean exactamente iguales.
En la identidad propuesta, vamos a transformar el lado izquierdo de la igualdad, para lo cual expresamos ctg x y sec x en términos de seno y coseno de la siguiente manera:
ctg x = cos x / sen x
sec x = 1 /cos x
Sustituimos esta expresión en el lado izquierdo de la identidad y simplificamos:
sen x . (1/cos x). (cos x / sen x) = (sen x. cos x / cos x . sen x) = 1
Y ya está comprobada la veracidad de la identidad.
Hay varias clases de identidades trigonométricas. A continuación describiremos brevemente las principales:
Distinguimos dos tipos de identidades fundamentales:
I) Las que se expresan a través de las razones básicas seno, coseno y tangente:
- sec x = 1 /cos x
- cosec x / 1 /sen x
- ctg x = 1 / tg x
- tg x = sen x /cos x
- ctg x = cos x / sen x
II) Las que se derivan de la paridad. Sabemos a través de su gráfica que sen x es una función impar, lo cual significa que:
sen (-x) = – sen x
Por su parte cos x es una función par, por lo tanto:
cos (-x) = cos x
Entonces:
tg (-x) = sen (-x) / cos (-x) = -sen x / cos x
De igual forma:
- cotg (-x) = -ctg x
- sec (-x) = sec x
- cosec (-x) = – cosec x
Son las que se obtienen a partir de la aplicación del teorema de Pitágoras al triángulo rectángulo de catetos a y b e hipotenusa c. Veamos:
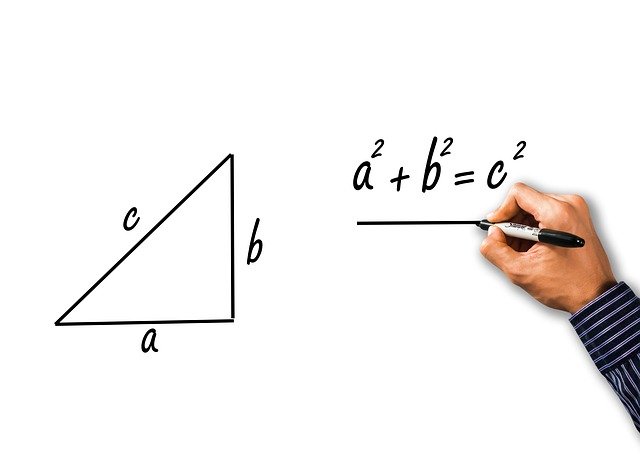
El teorema de Pitágoras afirma que:
c2 = a2 + b2
Dividiendo todo entre c2:
c2 / c2 = (a2 / c2) + (b2 / c2)
El término a la izquierda es 1 y recordando que seno y coseno del ángulo agudo α se definen como:
sen α = a/c
cos α = b/c
Resulta:
1 = (sen α)2 + (cos α)2
Esta identidad se conoce como identidad fundamental.
El procedimiento se puede llevar a cabo dividiendo entre a2 y b2, lo que da lugar a dos identidades más:
sec2 α =1 + tg2 α
cosec2 α =1 + ctg2 α
Las principales identidades trigonométricas para coseno, seno y tangente de la suma y la resta son las siguientes:
Demostración de sen (α + β) y cos (α + β)
Estas identidades se pueden demostrar geométricamente o también mediante la fórmula de Euler:
eiα = cos α + i sen α
Veamos lo que le sucede a la fórmula al sustituir la suma de dos ángulos α y β:
ei(α +β) = cos (α + β) + i sen (α + β)
Esta expresión es compleja, su parte real es cos (α+β) y su parte imaginaria es i sen (α + β). Guardamos este resultado para usarlo luego y nos concentramos en desarrollar la parte exponencial:
ei(α +β) = eiα ⋅ eiβ = (cos α + i sen α) . (cos β + i sen β) =
= cos α⋅cos β + cos α⋅i sen β + i⋅sen α cos β – sen α⋅sen β
La parte real de esta expresión es la que no está multiplicada por la unidad imaginaria “i”:
cos α⋅cos β – sen α. sen β
La parte imaginaria por lo tanto es:
i (cos α⋅sen β + sen α⋅cos β)
Para que dos expresiones complejas sean iguales, la parte real de una debe ser igual a la parte real de la otra. Lo mismo sucede con las partes imaginarias.
Tomamos el resultado guardado y lo comparamos con este:
cos α. cos β – sen α. sen β = cos (α + β)
i (cos α⋅sen β + sen α⋅cos β) = i sen (α + β)
sen (α + β) = (cos α. sen β + sen α⋅cos β)
En las fórmulas anteriores tomamos β = α y desarrollamos:
sen (α + α) = sen 2 α = sen α⋅cos α + cos α. sen α = 2⋅ sen α ⋅ cos α
cos (α + α) = cos 2 α = cos α⋅cos α – sen α⋅sen α = cos2 α – sen 2 α
tg (α + α) = tg 2 α = [tg α + tg α] / [1- tg α⋅tg α] = 2tg α / 1- tg2 α
Si en la segunda expresión se sustituye cos2 α = 1 – sen2 α se obtiene:
cos 2 α = cos2 α – (1- cos2 α) = 2 cos2 α -1
En esta última expresión sustituyamos α por α/2, queda lo siguiente:
cos α = 2 cos 2(α/2) -1
Despejando:
Demostrar que:
Vamos a trabajar algebraicamente el término izquierdo para que se parezca al derecho. Como en el término derecho aparece sen x, el primer paso es expresar cos2x en términos de sen x para que todo quede en términos de una misma razón trigonométrica:
Seguidamente se factoriza 1 – sen2 x por ser una diferencia de cuadrados perfectos. Para ello se despeja de la identidad fundamental:
cos2x = 1 – sen2 x
1 – sen2 x = (1- sen x)(1+senx)
Y se sustituye la factorización en la expresión original:
El término (1- senx) se simplifica y queda una igualdad:
1 + sen x = 1 + senx
Resolver la siguiente ecuación trigonométrica y dar la solución para valores comprendidos entre 0 y 360º:
tg x + sec2 x = 3
Solución
En el término de la izquierda hay dos razones trigonométricas, por lo tanto hay que reducir todo a una sola, con la finalidad de poder despejar la incógnita. El término sec2 x se expresa a través de una de las identidades pitagóricas:
sec2 α =1 + tg2 α
Al sustituir en la ecuación queda:
tg x + 1 + tg2 x = 3
Reordenando los términos:
tg2 x + tg x + 1 = 3
Esta ecuación se resuelve haciendo el cambio de variable:
tg x = u
u2 + u + 1 – 3 = 0 → u2 + u – 2 = 0
Esta ecuación de segundo grado se resuelve fácilmente por factorización:
(u +2) (u-1) = 0
Por lo tanto u1 = -2 y u2 = 1, que equivale a:
tg x1 = -2
tg x2 = 1
Finalmente:
x1 = arctg (-2) = 296.6º
x2 = arctg (1) = 45º
- Carena, M. 2019. Manual de Matemática Preuniversitaria. Universidad Nacional del Litoral.
- Figuera, J. 1999. Matemática. 1ro. Diversificado. Ediciones Colegial Bolivariana.
- Hoffman, J. Selección de temas de Matemática. Volumen 4.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Wikipedia. Identidades y fórmulas de trigonometría. Recuperado de: es.wikipedia.org.
- Zapata, F. 4 formas de resolver una ecuación de segundo grado. Recuperado de: francesphysics.blogspot.com.
- Zill, D. 1984. Álgebra y Trigonometría. McGraw Hill.
