Ángulos y triángulos: qué son, elementos y tipos de cada uno

¿Qué son ángulos y triángulos?

Un ángulo es la región del plano delimitada por dos semirrectas con un punto de origen en común. A este punto se le conoce como el vértice, mientras que las semirrectas reciben el nombre de lados. Por otra parte, un triángulo es una figura de tres ángulos y tres lados, con tres vértices.

Hablaremos primero de los ángulos.

Ángulos

Existen varias maneras de denotar los ángulos: a través de letras griegas como α, β, γ, a las que se puede añadir un acento circunflejo; con letras latinas mayúsculas o minúsculas, A, B, C, a, b, c; números, como 1, 2, 3… o empleando el símbolo para ángulo ∠.

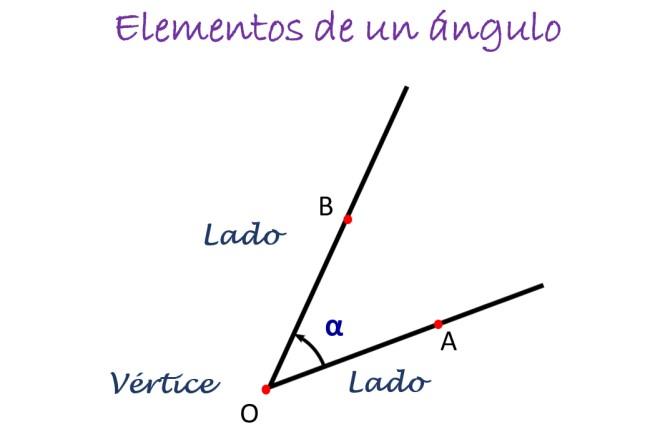
En la figura de arriba, el ángulo se mide desde el lado A hasta el B, indicado por el sentido de la flecha, y en el centro se coloca la letra que denota al vértice, que normalmente es O. El ángulo se denota entonces como ∠ AOB.

Cuando el ángulo se mide en sentido antihorario, se le asigna arbitrariamente un signo +, y si se mide en sentido horario, un signo –, para distinguirlos.

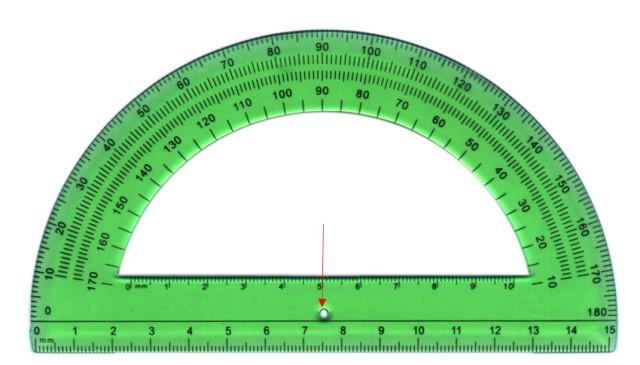
La medida de los ángulos se lleva a cabo mediante un transportador, que consiste en una lámina plástica semicircular como la que se muestra a continuación. El semicírculo se divide en 180 partes iguales, cada una llamada grado.

Para medir, se hace coincidir el vértice del ángulo con el punto central del transportador, indicado con la flecha, y el lado inicial con uno de los bordes, interno o externo. El lado final intersecta alguna de las marcas del transportador, siendo dicha medida la del ángulo.

Tipos de ángulos

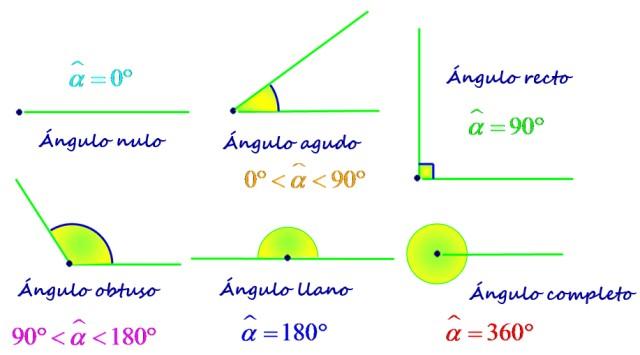
Uno de los criterios más utilizados para clasificar ángulos, es según su medida. Por tanto, un ángulo puede ser:

• Nulo, mide 0º.
• Agudo, cuya medida está comprendida entre 0 y 90º.
• Recto, mide exactamente 90º.
• Obtuso, es mayor que 90º y menor que 180º.
• Llano, su medida es igual a 180º.
• Completo, representa una vuelta completa y mide 360º.

De acuerdo a la relación entre su medida y la del ángulo llano, que es 180º, los ángulos también se pueden clasificar en:

• Cóncavos, si mide menos de 180º. Por lo tanto, los ángulos agudos, rectos y obtusos son cóncavos, pues su medida siempre es menor a 180º (ver la figura de arriba).
• Convexos, si su medida es mayor a 180º, como los ángulos de 270º y 360º.

Ángulos según la suma de sus medidas y según la posición de sus lados

Dos ángulos ∠ A y ∠ B pueden ser:

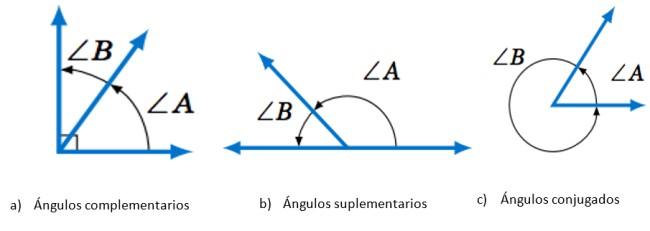
• Complementarios, si la suma de sus medidas es igual a 90º.
• Suplementarios, cuando al sumar las respectivas medidas se obtiene 180º.
• Conjugados, si dicha suma es igual a 360º.

En cuanto a la posición de sus lados, dos ángulos pueden ser:

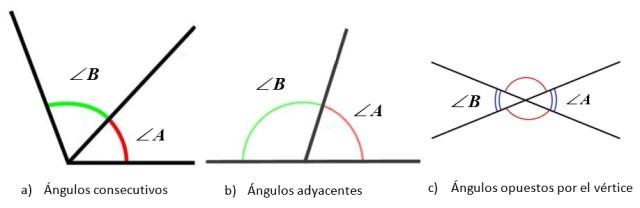
• Consecutivos, cuando tienen en común el vértice y uno de los lados.
• Adyacentes, si son consecutivos, pero los lados no comunes son opuestos, por lo que son también suplementarios.
• Opuestos por el vértice, cuando tienen el vértice común, y los lados de los ángulos se prolongan en sentido opuesto.

Triángulos

El triángulo es una figura geométrica plana y cerrada, perteneciente a la familia de los polígonos, con tres lados conformados por rectas que se cortan dos a dos, generando tres ángulos.

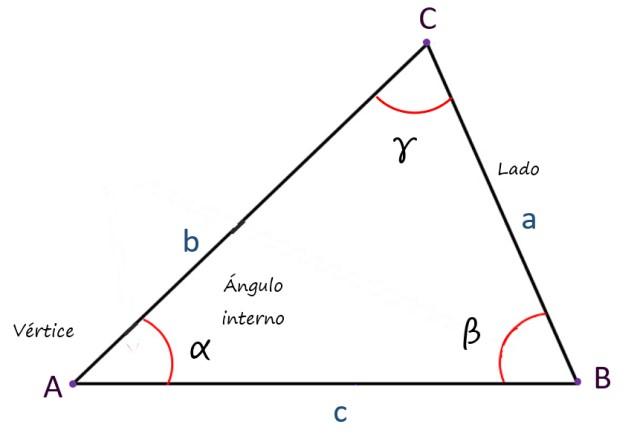
Sus elementos básicos son:

• Vértices, que son los puntos de intersección de las mencionadas rectas.
• Lados, un total de 3 y que consisten en los segmentos de rectas que conectan a los vértices.
• Ángulos internos, también en número de 3, cuya suma siempre es igual a 180º.

Generalmente, los lados se denotan con letras latinas minúsculas, los vértices con mayúsculas y los ángulos con letras griegas minúsculas, pero otras notaciones también son posibles.

Tipos de triángulos

Triángulos según la forma de sus lados

Según este criterio, los triángulos pueden ser:

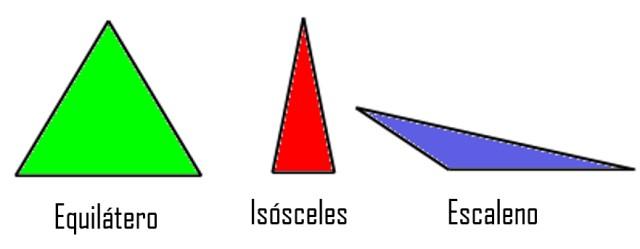
• Equiláteros, si sus tres lados tienen la misma medida.
• Isósceles, cuando solamente dos de los lados tienen igual medida, mientras que el tercero es diferente.
• Escaleno, si los tres lados tienen diferente tamaño.

Triángulos según sus ángulos internos

Este criterio se basa en los tipos de ángulo interno del triángulo. De acuerdo a esto, un triángulo puede ser:

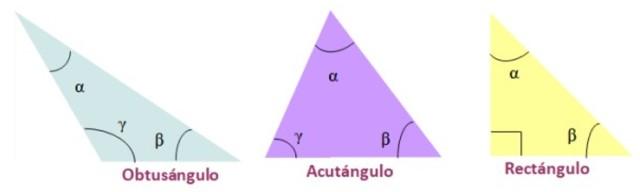
• Acutángulo, cuando los tres ángulos internos del triángulo son agudos.
• Rectángulo, si el triángulo tiene un ángulo interno de medida igual a 90º.
• Obtusángulo, uno de los ángulos internos del triángulo es obtuso.

Segmentos notables del triángulo

Entre los segmentos notables de cualquier triángulo, se tienen:

• Mediana, segmento dirigido desde un vértice, directamente hasta el lado opuesto.
• Mediatriz, es un segmento perteneciente a la recta perpendicular al lado, la cual intersecta al punto medio de dicho lado.
• Bisectriz, segmento que divide un ángulo interno en dos partes iguales, y que se prolonga hasta el lado opuesto al ángulo.
• Altura, segmento perpendicular a un lado, el cual se prolonga hasta el vértice opuesto.

Pueden trazarse tres medianas, tres mediatrices y así sucesivamente.

Centros del triángulo

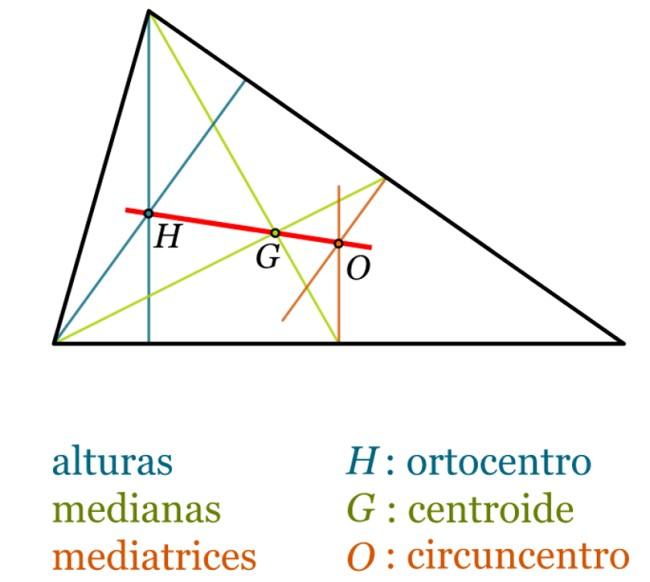
En cualquier triángulo, destacan los siguientes puntos (véase la siguiente figura):

• Baricentro G, también llamado a veces centroide del triángulo, es el punto de intersección de las medianas y siempre es interior al triángulo.
• Ortocentro H, punto en el que se intersectan las tres alturas.
• Circuncentro O, es el punto de intersección de las mediatrices. Puede encontrarse en el exterior del triángulo, si este es obtusángulo, mientras que, en el triángulo rectángulo, O coincide con el punto medio de la hipotenusa.
• Incentro, punto de intersección de las bisectrices del triángulo.
• Recta de Euler, recta que une al baricentro, el ortocentro y el circuncentro, en cualquier triángulo que no sea equilátero. Se cumple siempre que la longitud del segmento HG es el doble que la del segmento GO.

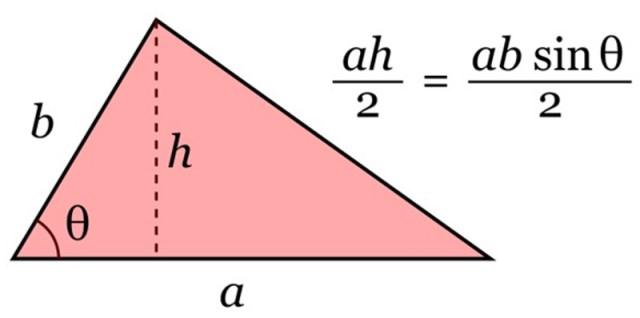
Área de un triángulo

Para calcular el área A del triángulo, se emplea la siguiente fórmula, de carácter general:

A = base × altura / 2

Fórmula de Herón

Conociendo la longitud de todos los lados del triángulo, la siguiente fórmula, conocida como fórmula de Herón, permite hallar el área A:

Referencias

1. Alexander, D. 2013. Geometría. 5ta. Edición. Cengage Learning.
2. Angles. Mathematics Libretexts. Recuperado de: math.libretexts.org.
3. Jiménez, René. 2010. Matemáticas II (Geometría y trigonometría). 2da. Edición. Pearson.
4. Universo Fórmulas. Triángulo. Recuperado de: universoformulas.com.
5. Zapata, F. Triángulos: historia, elementos, clasificación, propiedades. Recuperado de: lifeder.com.