Tetradecágono: propiedades, cómo se hace, ejemplos
¿Qué es un tetradecágono?
El tetradecágono es una figura geométrica plana y cerrada de 14 lados, perteneciente a la familia de los polígonos. También se conoce con el nombre de tetrakaidecágono, todos vocablos derivados de palabras griegas: “tetra” (cuatri), “kai” (más), “deca” (diez) y “gon” (ángulo), ya que también tiene 14 ángulos interiores.
En la figura se muestra un tetradecágono regular, es decir, uno cuyos lados y ángulos internos tienen todos la misma medida, mostrando las principales características de esta figura.
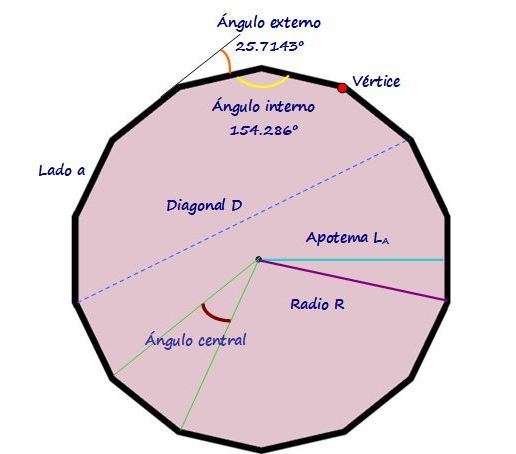
Elementos del tetradecágono
- Lados: se llaman así a los 14 segmentos de recta que se cierran para conformar la figura. Pueden tener todos la misma longitud, en cuyo caso el polígono es regular, o pueden ser distintos y entonces se tiene un tetradecágono irregular.
- Vértices: son los puntos de intersección entre segmentos sucesivos y el tetradecágono tiene 14 vértices.
- Centro: punto equidistante de los vértices.
- Radio: segmento que une al centro con un vértice.
- Ángulo interno: se forma por la parte interior de la figura y entre dos segmentos sucesivos o adyacentes. Mide 154.286º para el tetradecágono regular, sin importar el tamaño que tenga el lado.
- Ángulo externo: formado entre un lado y la prolongación de uno de los lados adyacentes. Sin importar la longitud del lado, este ángulo mide 25.7143º para un tetradecágono regular.
- Ángulo central: el que tiene su vértice en coincidencia con el centro del polígono y sus lados son dos radios consecutivos.
- Diagonal: segmento que conecta dos vértices no consecutivos.
¿Cómo se hace un tetradecágono?
Los polígonos regulares de n lados que se construyen con regla y compás tienen a n de la forma 2r p1…pk, siendo los pi números primos de Fermat distintos, y a su vez los números primos de Fermat toman la forma 2n + 1.
El tetradecágono tiene n =14 lados, pero 14 = 7×2, que no son primos de Fermat, porque no se pueden expresar de la forma indicada. Por lo tanto este polígono no admite construcción exacta con regla y compás, pero sí una construcción que se aproxima muy bien, mediante varios métodos.
Método general para construir polígonos regulares
El siguiente es un método general (no es el único) para construir polígonos regulares inscritos en una circunferencia, entre ellos el tetradecágono regular.
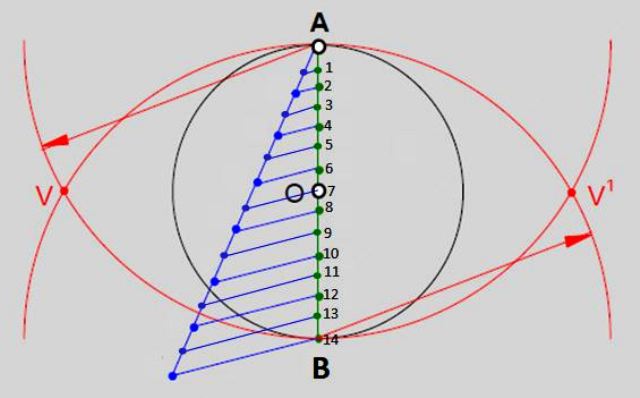
Consiste en dividir el diámetro vertical de dicha circunferencia en tantas partes iguales como lados tiene el polígono a dibujar. En el caso del tetradecágono serán las 14 partes numeradas en la imagen 2. Estos son los pasos:
- Trazar un diámetro vertical que va desde A hasta B.
- Seguidamente trazar una semirrecta partiendo desde el punto A, abrir el compás con apertura arbitraria y hacer 14 divisiones igualmente espaciadas sobre ella. La semirrecta y sus divisiones pueden salir de la circunferencia.
- Unir la marca 14va (en azul en la imagen) al final de la semirrecta con el punto B.
- Proseguir uniendo el resto de las marcas en la semirrecta con los respectivos puntos sobre el diámetro vertical (puntos de color verde).
- Con la punta del compás en A y apertura igual a la medida del diámetro de la circunferencia se traza un arco. Con la misma medida, pero apoyando la punta en B (punto 14 de la figura 2) se traza otro arco, que se corta con el primero en los puntos V y V’ señalados.
- Ahora, con la regla trazar una línea desde V’ hasta el punto 2 y prolongarla hasta intersectar la circunferencia en el punto C de la figura 3. Marcar el punto de intersección, que será uno de los vértices de la figura.
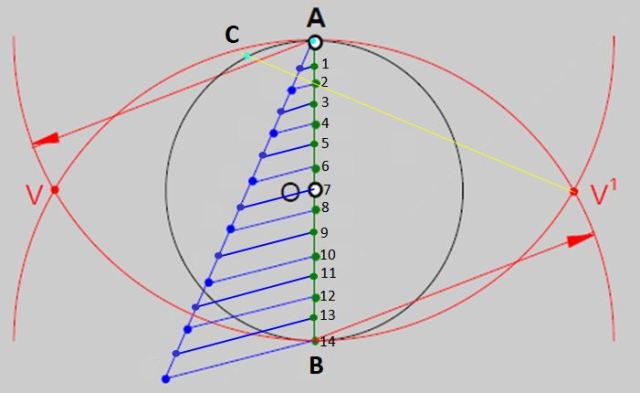
- Abrir el compás en la distancia AC y apoyando la punta en A o en C, ir trazando arcos de igual medida sobre toda la circunferencia, de esta manera queda dividida en 14 partes aproximadamente iguales, las intersecciones entre los arcos y la circunferencia son los vértices del tetradecágono.
- Con una regla unir los vértices con segmentos de recta, formando los lados del polígono.
- Borrar cuidadosamente las construcciones auxiliares.
En la siguiente animación se muestra otro método también aproximado, con regla y compás:

Fórmulas para el tetradecágono regular
Las siguientes fórmulas son válidas para los polígonos regulares:
- Número de lados: n
- Medida del lado: a
- Apotema: LA
- Radio: R
- Perímetro: P
- Área: A
- Ángulo interno: I
- Ángulo externo: E
- Diagonales: D
Lado conocida la apotema
a = 2LA × tg (π/n)
Para n = 14:
a = 2LA × tg (π/14)
Lado conocido el radio
a =2R × sen (π/n)
Si n = 14:
a =2R × sen (π/14)
Perímetro conocido el lado
El perímetro es la suma de los lados. Cuando el tetradecágono es regular:
P = n⋅a = 14⋅a
Si el tetradecágono es irregular hay que sumar directamente todos los lados para obtener el perímetro.
Área conocido el lado
A= ¼ na2 × cot (π/n)
Para n = 14:
A= ¼ (14a2)× cot (π/14) = (7/2) a2 × cot (π/14)
Área conocida la apotema
A= n⋅LA2 × tg (π/n)
Tomando n = 14 resulta:
A= 14LA2 × tg (π/14)
Área en función del perímetro y la apotema
A = (P × LA)/2
Medida del ángulo interior
I = 12 × 180º /14 = 154.286º
Medida del ángulo exterior
E = 360º/n
Cuando n = 14 se tiene:
E = 25.7143º
Diagonales
La fórmula para calcular el número de diagonales presentes en cualquier polígono, regular o no, es:
Para n = 14:
D = 14× 11/2 = 77 diagonales
Ejemplos

Los polígonos regulares aparecen repetidamente en numerosos diseños, como por ejemplo monedas. En el caso de tetradecágono regular, este aparece en monedas conmemorativas de Malasia, representando sus lados a cada uno de los catorce estados confederados de esa nación.
Tetradecágonos cóncavos y convexos
En general, los polígonos como el tetradecágono pueden ser convexos o cóncavos, en el primer caso, la medida de sus ángulos internos no supera los 180º. El tetradecágono regular es convexo, como todo polígono regular, ya que cualquiera de sus ángulos internos mide 154.286º.
En cambio, en el tetradecágono cóncavo, uno o más de sus ángulos internos mide más de 180º.
Ejemplo numérico
Dado un tetradecágono regular cuyo lado mide 5 cm, encontrar:
a) Perímetro
b) Medida de la apotema
c) Longitud del radio
d) Área
Respuestas
a) Como se trata de un polígono regular, el perímetro es:
P = 14 × 5 cm = 70 cm.
b) De la ecuación a = 2LA × tg (π/14), donde a = 5 cm, se despeja la apotema LA:
LA = a / [2× tg (π/14)] = 5 cm / 0.4565 = 21.9064 cm
c) El radio R se puede calcular mediante a = 2R × sen (π/14):
R = a / [2× sen (π/14)] = 5 cm / 0.4565 = 22.4698 cm
d) Hay varias alternativas para el área, por ejemplo A = (P × LA)/2:
A = (70×21.9064)/2 cm2 = 1533.45 cm2.
Referencias
- Alexander, D. 2013. Geometría. 5ta. Edición. Cengage Learning.
- Arturo Geometría. Método general para dibujar polígonos inscritos en circunferencias. Recuperado de youtube.com
- Calculator Soup. Regular Polygon Calculator. Recuperado de: calculatorsoup.com.
- DibujoTecni. Polígonos regulares. Recuperado de: dibujotecni.com.
- Requena, B. Polígono cóncavo. Recuperado de: universoformulas.com.
- Wikipedia. Polígono construible. Recuperado de: es.wikipedia.org.
