Descomposición aditiva: concepto, aplicaciones, particiones, gráficas

La descomposición aditiva de un número entero positivo consiste en expresarlo como una suma de dos o más números enteros positivos. Así, tenemos que el número 5 podemos expresarlo como 5= 1+4, 5= 2+3 o 5= 1+2+2. Cada una de estas maneras de escribir el número 5 es lo que llamaremos descomposición aditiva.
Si prestamos atención podemos ver que las expresiones 5 = 2+3 y 5 = 3+2 representan la misma composición; ambas cuentan con los mismos números. Sin embargo, solo por una cuestión de comodidad se suele escribir cada uno de los sumandos siguiendo el criterio de menor a mayor.
Descomposición aditiva
Como otro ejemplo podemos tomar el número 27, el cual podemos expresarlo como:
27= 7+10+10
27= 9+9+9
27= 3+6+9+9
27= 9+18
La descomposición aditiva es una herramienta de gran utilidad que nos permite reforzar nuestros conocimientos sobre los sistemas de numeración.
Descomposición aditiva canónica
Cuando tenemos números de más de dos cifras, una forma particular de descomponerlos es en los múltiplos de 10, 100, 1000, 10 000, etc., que lo conforman. Esta forma de escribir un número cualquiera es llamada descomposición aditiva canónica. Por ejemplo, el número 1456 podemos descomponerlo como sigue:
1456 = 1000 + 400+ 50 + 6
Si tenemos el número 20 846 295, su descomposición aditiva canónica será:
20 846 295= 20 000 000 + 800 000 + 40 000 + 6000 + 200 + 90 +5.
Gracias a esta descomposición, podemos ver que el valor de un dígito dado viene dado por la posición que ocupa. Tomemos como ejemplo los números 24 y 42:
24= 20 + 4
42= 40 +2
Aquí podemos observar que en 24 el 2 tiene un valor de 20 unidades y el 4 un valor de 4 unidades; en cambio, en el 42 el 4 tiene un valor de 40 unidades y el 2 de dos unidades. Así, aunque ambos números usan los mismos dígitos, sus valores son totalmente distintos por la posición que ocupan.
Aplicaciones
Una de las aplicaciones que podemos darle a la descomposición aditiva es en cierto tipo de demostraciones, en las cuales nos es muy útil ver a un número entero positivo como suma de otros.
Teorema de ejemplo
Tomemos como ejemplo el siguiente teorema con sus respectivas demostraciones.
– Sea Z un número entero de 4 dígitos, entonces Z es divisible por 5 si su cifra correspondiente a las unidades es cero o cinco.
Demostración
Recordemos lo que es divisibilidad. Si tenemos “a” y “b” números enteros, decimos que “a” divide a “b” si existe un entero “c” tal que b = a*c.
Una de las propiedades de la divisibilidad nos dice que si “a” y “b” son divisibles entre “c”, entonces la resta “a-b” también lo es.
Sea Z un número entero de 4 dígitos; por lo tanto, podemos escribir a Z como Z = ABCD.
Usando la descomposición aditiva canónica tenemos que:
Z= A*1000 + B*100 + C*10 + D
Es claro que A*1000 + B*100 + C*10 es divisible entre 5. Por esto tenemos que Z es divisible entre 5 si Z – (A*1000 + B*100 + C*10) es divisible entre 5.
Pero Z – (A*1000 + B*100 + C*10) = D y D es un número de una sola cifra, por lo cual la única forma de que sea divisible entre 5 es que sea 0 o 5.
Por lo tanto, Z es divisible entre 5 si D = 0 o D = 5.
Notemos que si Z tiene n dígitos la demostración es exactamente la misma, solo cambia que ahora escribiríamos Z=A1A2…An y el objetivo sería probar que An es cero o cinco.
Particiones
Decimos que una partición de un número entero positivo es una manera en la que podemos escribir un número como suma de enteros positivos.
La diferencia entre una descomposición aditiva y una partición es que, mientras en la primera se busca que al menos se pueda descomponer en dos sumandos o más, en la partición no se tiene esta restricción.
Así, tenemos lo siguiente:
5=5
5= 1+4
5= 2+3
5= 1+2+2
Las anteriores son particiones de 5.
Es decir, tenemos que toda descomposición aditiva es una partición, pero no toda partición es necesariamente una descomposición aditiva.
En teoría de números, el teorema fundamental de la aritmética nos garantiza que todo número entero se puede escribir de manera única como producto de primos.
Cuando se estudian las particiones, el objetivo es determinar de cuántas maneras se puede escribir un entero positivo como suma de otros enteros. Por ello definimos la función partición como se presenta a continuación.
Definición
La función partición p(n) se define como el número de maneras en que un entero positivo n se puede escribir como una suma de enteros positivos.
Volviendo al ejemplo del 5, tenemos que:
5=5
5= 1+4
5= 2+3
5= 1+1+3
5= 1+2+2
5= 1+1+1+2
5= 1+1+1+1+1
De tal manera, p(5) = 7.
Gráficas
Tanto las particiones como las descomposiciones aditivas de un número n pueden representarse geométricamente. Supongamos que tenemos una descomposición aditiva de n. En dicha descomposición pueden arreglarse los sumandos de manera que los miembros de la suma estén ordenados de menor a mayor. Entonces, vale que:
n = a1 + a2 + a3 +… + ar con
a1 ≤ a2 ≤ a3 ≤… ≤ ar.
Podemos graficar dicha descomposición de la siguiente manera: en una primera fila marcamos los a1-puntos, luego en la siguiente marcamos a2-puntos, y así sucesivamente hasta llegar a ar.
Tomemos como ejemplo el número 23 y su siguiente descomposición:
23= 5 + 4 + 7 + 3 + 1 +3
Ordenamos dicha descomposición y tenemos:
23= 1 + 3 + 3 + 4+ 5 + 7
Su gráfica correspondiente sería:
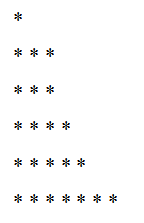
Así mismo, si leemos dicha gráfica de manera vertical en vez de forma horizontal, podemos obtener una descomposición que posiblemente sea distinta a la anterior. En el ejemplo del 23 destaca lo siguiente:
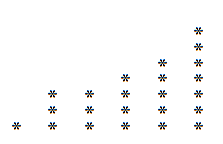
Por lo que tenemos que 23 también podemos escribirlo como:
23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.
