Funciones trigonométricas inversas: valor, derivadas, ejemplos, ejercicios
Las funciones trigonométricas inversas, tal como su nombre lo indica, son las correspondientes funciones inversas de las funciones seno, coseno, tangente, cotangente, secante y cosecante.
Las funciones trigonométricas inversas se denotan con el mismo nombre de su correspondiente función trigonométrica directa más el prefijo arc. De esta forma:
1.- arcsen(x) es la función trigonométrica inversa de la función sen(x)
2.- arccos(x) es la función trigonométrica inversa de la función cos(x)
3.- arctan(x) es la función trigonométrica inversa de la función tan(x)
4.- arccot(x) es la función trigonométrica inversa de la función cot(x)
5.- arcsec(x) es la función trigonométrica inversa de la función sec(x)
6.- arccsc(x) es la función trigonométrica inversa de la función csc(x)
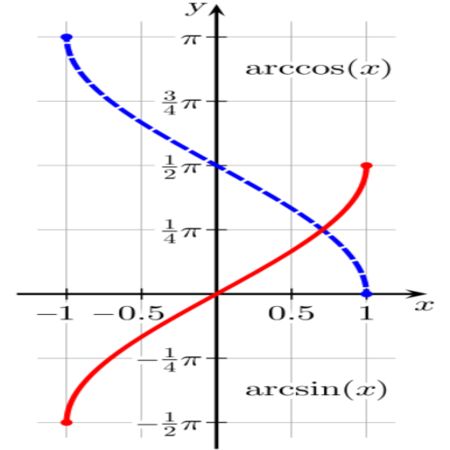
La función θ = arcsen(x) da como resultado un arco unitario θ (o ángulo en radianes θ) tal que sen(θ) = x.
Así por ejemplo, arcsen(√3/2) = π/3 ya que como es sabido, el seno de π/3 radianes es igual a √3/2.
Índice del artículo
- 1 Valor principal de las funciones trigonométricas inversas
- 2 Derivadas de las funciones trigonométricas inversas
- 3 Ejemplos
- 4 Ejercicios
- 5 Referencias
Para que una función matemática f(x) tenga inversa g(x) = f-1(x) es necesario que dicha función sea inyectiva, lo cual significa que cada valor y del conjunto de llegada de la función f(x) proviene de uno y solo un valor x.
Es claro que este requisito no lo cumple ninguna función trigonométrica. Para aclarar el punto, notemos que el valor y = 0,5 puede obtenerse de la función seno de las siguientes maneras:
- sen(π/6) = 0,5
- sen(5π/6) = 0,5
- sen(7π/6) = 0,5
Y muchas más, ya que la función seno es periódica con periodo 2π.
Para poder definir las funciones trigonométricas inversas, es necesario restringir el dominio de sus correspondientes funciones trigonométricas directas, de modo tal que cumplan el requisito de inyectividad.
Ese dominio restringido de la función directa será el rango o rama principal de su correspondiente función inversa.
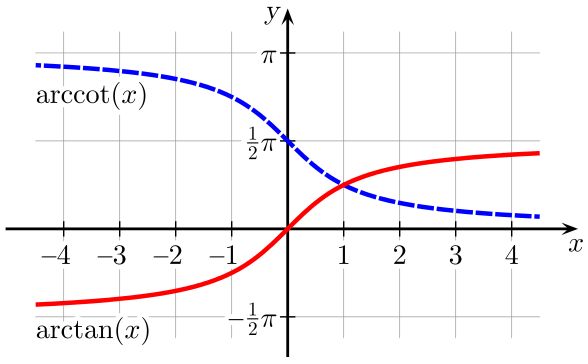
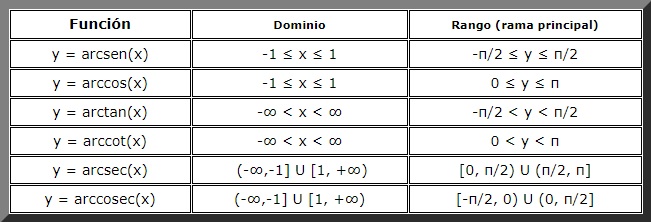
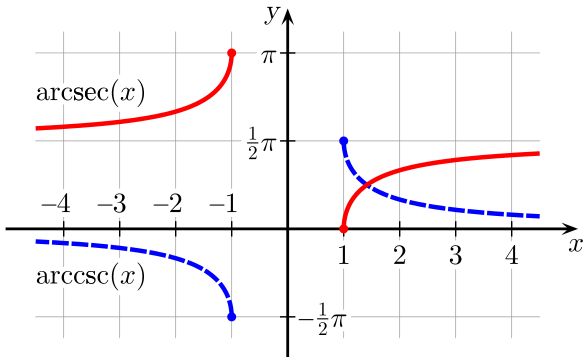
Para obtener las derivadas de las funciones trigonométricas inversas se aplican las propiedades de las derivadas, en particular la derivada de una función inversa.
Si denotamos por f(y) a la función y por f-1(x) a su función inversa, entonces la derivada de la función inversa se relaciona con la derivada de la función directa mediante la siguiente relación:
[f-1(x)]’ = 1/ f’[f-1(x)]
Por ejemplo: si x = f(y) = √y es la función directa, su inversa será
y = f-1(x) = x2. Apliquemos la regla de la derivada de la inversa a este sencillo caso para ver que efectivamente dicha regla se cumple:
[x2]’ = 1 / [√y]’= 1 / (½ y-½ = 2 y½ = 2 (x2)½ = 2x
Pues bien, podemos valernos de este truco para hallar las derivadas de las funciones trigonométricas inversas.
Por ejemplo, tomamos θ = arcsen(x) como la función directa, entonces su función inversa será sen(θ) = x.
[arcsen(x)]’ = 1 / [sen(θ)]’ = 1 / cos(θ) = 1 / √(1 – sen(θ)2) = …
…= 1 / √(1 – x2) .
De esta forma pueden obtenerse todas las derivadas de las funciones trigonométricas inversas, las cuales se muestran a continuación:

Estas derivadas son válidas para cualquier argumento z perteneciente a los números complejos y por tanto son válidas también para cualquier argumento real x, ya que z = x + 0i.
Hallar arctan(1).
Solución
El arctan(1) es el arco unitario (ángulo en radianes) ፀ tal que la tan(ፀ) = 1. Ese ángulo es ፀ = π/4 porque tan(π/4) = 1. Entonces arctan(1) = π/4.
Calcular arcsen( cos(π/3) ).
Solución
El ángulo π/3 radianes es un ángulo notable cuyo coseno es ½, de modo que el problema se reduce a hallar arcsen( ½ ).
Entonces se trata de encontrar cual es el ángulo cuyo seno da ½. Ese ángulo es π/6, ya que sen(π/6) = sen(30º) = ½. Por tanto arcsen( cos(π/3) ) = π/6.
Hallar el resultado de la siguiente expresión:
sec( arctan(3) ) + csc( arccot(4) )
Solución
Comenzamos por nombrar α = arctan(3) y β = arccot(4). Entonces la expresión que tenemos que calcular queda así:
sec(α) + csc(β)
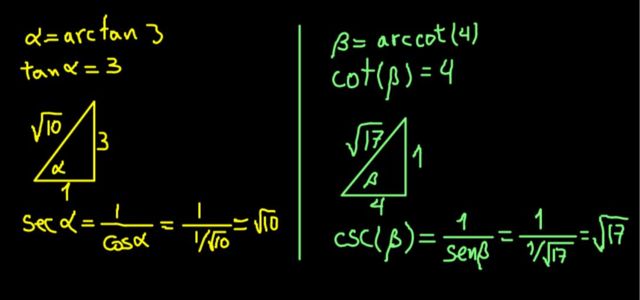
La expresión α = arctan(3) equivale a decir tan(α) = 3.
Como la tangente es el cateto opuesto sobre el adyacente, se construye un triángulo rectángulo de cateto opuesto a α de 3 unidades y un cateto adyacente de 1 unidad, de modo que tan(α) = 3/1 = 3.
En un triángulo rectángulo la hipotenusa se determina por el teorema de Pitágoras. Con estos valores resulta √10, de modo que:
sec(α) = hipotenusa / cateto adyacente = √10 / 1 = √10.
De forma semejante β = arccot(4) es equivalente a afirmar que cot(β) = 4.
Se construye un triángulo rectángulo de cateto adyacente a β de 4 unidades y un cateto opuesto de 1 unidad, de modo que cot(β) = 4/1.
De inmediato se completa el triángulo hallando su hipotenusa gracias al teorema de Pitágoras. En este caso resultó tener √17 unidades. Luego se calcula la csc(β) = hipotenusa / cateto opuesto = √17 / 1 = √17.
Recordando que la expresión que debemos calcular es:
sec( arctan(3) ) + csc( arccot(4) ) = sec(α) + csc(β) = …
…= √10 + √17 = 3,16 + 4,12 = 7,28.
Hallar las soluciones de:
Cos(2x) = 1 – Sen(x)

Solución
Es necesario que todas las funciones trigonométricas queden expresadas en el mismo argumento o ángulo. Usaremos la identidad del ángulo doble:
Cos(2x) = 1 – 2 Sen2(x)
Entonces la expresión original queda reducida a:
1 – 2 Sen2(x) = 1 – Sen x
Una vez simplificada y factorizada se expresa como:
sen(x) (2 sen(x) – 1) = 0
Que da lugar a dos ecuaciones posibles: Sen(x) = 0 con solución x=0 y otra ecuación sen(x) = ½ con x = π/6 como solución.
Las soluciones a la ecuación planteada son: x = 0 o x = π/6.
Hallar las soluciones de la siguiente ecuación trigonométrica:
cos(x) = sen2(x)
Solución
Para resolver esta ecuación es conveniente colocar un solo tipo de función trigonométrica, por lo que usaremos la identidad trigonométrica fundamental de modo que la ecuación original queda reescrita de la siguiente manera:
cos(x) = 1 – cos2(x)
Si nombramos y = cos(x), la expresión puede se reescrita como:
y2 + y – 1 = 0
Es una ecuación de segundo grado en y, cuyas soluciones son:
y = (-1 ± √5) / 2
Entonces los valores de x que cumplen la ecuación original son:
x = arccos( (-1 ± √5) / 2 )
Siendo la solución real la de signo positivo x = 0,9046 rad = 51,83º.
La otra solución es compleja: x = (π – 1,06 i) rad.
- Hazewinkel, M. 1994. Encyclopaedia of Mathematics. Kluwer Academic Publishers / Springer Science & Business Media.
- Mate Movil. Funciones trigonométricas inversas. Recuperado de: matemovil.com
- Universo fórmulas. Funciones trigonométricas inversas. Recuperado de: universoformulas.com
- Weisstein, Eric W. Inverse Trigonometric Functions. Recuperado de: mathworld.wolfram.com
- Wikipedia. Inverse trigonometric functions. Recuperado de: en.wikipedia.com
