Estadística
2021-09-11T22:38:19+02:00

Medidas de dispersión: qué y cuáles son, ejemplos

¿Qué son las medidas de dispersión?

Las medidas de dispersión o de variación, en estadística, miden cuánto se aleja una distribución de datos del valor de una medida central, como puede ser la media o promedio aritmético. Su valor siempre es positivo y normalmente distinto de 0, salvo en el caso de datos idénticos.

Si una medida de dispersión arroja un valor pequeño, significa que los datos se ubican muy cercanos al promedio, pero si es grande, quiere decir que los datos están más dispersos, por lo tanto, alejados de la media.

Las medidas de dispersión son muy importantes desde el punto de vista estadístico, no solo como indicadores aritméticos de la variación de los datos, sino como una ayuda inestimable cuando se quiere mejorar la calidad, tanto en la manufactura de productos como en la prestación de servicios.

Ejemplo de ello son las filas de atención en los bancos. El tiempo promedio que demoran los clientes cuando hacen una fila única y luego se distribuyen en las taquillas, es el mismo que si hacen líneas individuales frente a cada una.

Sin embargo, la dispersión es menor en la fila única, lo que significa que el tiempo de atención individual es muy parecido para cada cliente. Los clientes han declarado que se sienten más a gusto de esta manera, aun si el tiempo de atención promedio sea el mismo en cualquiera de las dos modalidades.

Principales medidas de dispersión

Las principales son: rango, varianza, desviación estándar y coeficiente de variación.

Rango

Se define el rango R de un conjunto de datos a la diferencia entre el valor máximo x_max y el valor mínimo x_min del conjunto:

Rango = R = Valor máximo – valor mínimo = x_max− x_min

El rango es rápido de calcular, pero es muy sensible a los valores extremos, y tiene la desventaja de no tomar en cuenta a los valores intermedios. Por ello se emplea únicamente para tener una idea inicial, bastante aproximada, de la dispersión de los datos.

Ejemplo de rango

Esta es una lista del número de huracanes ocurridos en el Atlántico durante los últimos 14 años:

8; 9; 7; 8; 15; 9; 6; 5; 8; 4; 12; 7; 8; 2

El dato de valor máximo es 15, y el valor mínimo es 2, por lo tanto:

R = Valor máximo – valor mínimo = x_max− x_min =15 – 2 = 13 huracanes

Varianza

Esta medida se utiliza para comparar a cada uno de los datos con la media del conjunto, y se calcula sumando las diferencias, elevadas al cuadrado, entre cada valor con la media y dividiendo entre el número total de valores.

Sea:

-La media: μ

-Un valor cualquiera, perteneciente al conjunto de datos: x_i

-El número total de observaciones: N

Denotando a la varianza de una población como σ², la expresión para calcularla es:

Y cuando se toma una muestra de tamaño n de una población, se prefiere calcular la varianza de este modo:

Por otro lado, la idea de elevar al cuadrado cada diferencia entre el dato y la media, es para evitar que al sumarlas resulte 0, ya que algunas diferencias serán positivas y otras negativas, lo que tiende a cancelar la suma. En cambio, los cuadrados siempre son positivos.

De allí que la varianza siempre sea positiva, aún si la diferencia entre x_iy la media es negativa, y su principal ventaja de la varianza es que toma en cuenta a cada dato del conjunto.

Pero tiene el inconveniente de que sus unidades no son las mismas que las de los datos, por ejemplo, si estos consisten en tiempos, medidos en minutos, la varianza del conjunto vendrá dada en minutos al cuadrado.

Ejemplo de varianza

El cálculo de la varianza requiere hallar la media. Tomando los datos del número de huracanes, la media se calcula mediante:

(8 + 9 + 7+ 8 + 15 + 9 + 6 + 5+ 8 + 4 + 12 + 7 + 8+ 2)/14 = 7.7 huracanes.Por lo tanto, la varianza es:

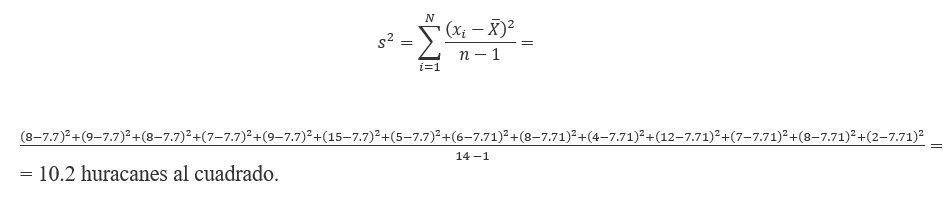
Desviación estándar

Para subsanar el problema de la falta de concordancia entre las unidades, se define la desviación estándar σ, como la raíz cuadrada de la varianza:

Y análogamente, en el caso de una muestra:

Existe una regla empírica para estimar el valor de la desviación estándar de un conjunto de datos muestrales, partiendo del rango. Según esta regla, la desviación estándar es, aproximadamente, la cuarta parte de R:

s ≈ R/4

Tiene la ventaja de permitir una rápida estimación de la desviación estándar, dado que las operaciones son mucho más sencillas.

La desviación estándar es, con mucho, la medida de dispersión más utilizada, por eso vale la pena destacar sus principales características:

La desviación estándar indica cuánto se alejan los datos de la media
Siempre es positiva, pero puede ser 0 si todos los datos son idénticos
A mayor valor de la desviación estándar, más dispersos están los datos
Las unidades de la desviación estándar son las mismas que las de la variable en estudio
Su valor cambia rápidamente cuando uno de los datos (o más), tiene un valor muy diferente al resto
Los valores de la desviación estándar son sesgados, es decir, los promedios de la desviación estándar no se distribuyen alrededor de la media, en contraste con la varianza, que es no sesgada.

Ejemplo de desviación estándar

Continuando con el ejemplo de los huracanes, la desviación estándar es:

O, si se prefiere utilizar la aproximación de la desviación estándar a través del rango, se obtiene un valor bastante cercano:

s = 13 / 4 = 3.25

Coeficiente de variación

El coeficiente de variación se denota por las iniciales CV o r, en algunos textos, y tanto para una población, como para una muestra, relaciona la desviación estándar y la media, como un porcentaje:

O bien:

Las ecuaciones son válidas siempre que la media sea distinta de 0.

Por regla general, el coeficiente de variación se redondea a un solo decimal, y se emplea para comparar datos de dos poblaciones diferentes.

Ejemplo de coeficiente de variación

Los tiempos de espera en segundos, para los clientes de un banco, se registran en dos situaciones: cuando hacen una fila única y cuando hacen filas individuales ante las taquillas de atención. Los resultados son los siguientes:

Ambos conjuntos de datos se pueden comparar a través de su coeficiente de variación respectivo:

Fila única

Media = 429 segundos
Desviación = 28.6 segundos
CV= (28.6/429) x 100 = 6.7 %

Filas individuales

Media = 429 segundos
Desviación = 109.3 segundos
CV= (109.3/429) x 100 = 25.5 %

Como este último valor es mayor, ello indica que hay más variabilidad en los tiempos de atención a los clientes cuando hacen filas individuales que cuando hacen una fila única, aunque el tiempo promedio es el mismo en cada caso.