Trinomio cuadrado perfecto: cómo identificarlo, ejemplos, ejercicios

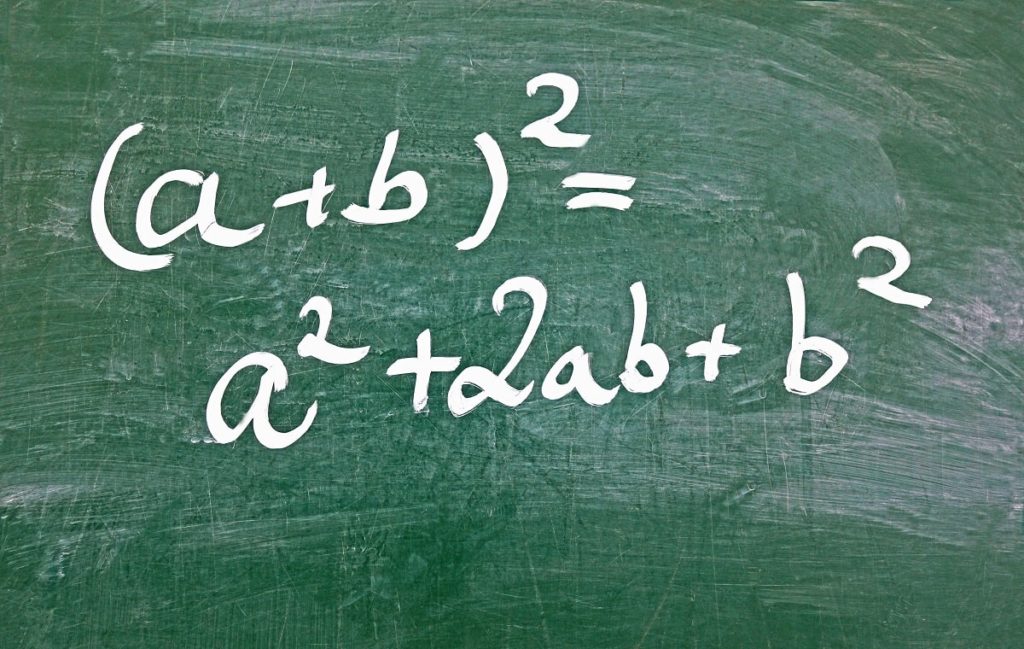
¿Qué es el trinomio cuadrado perfecto?

El trinomio cuadrado perfecto es aquel polinomio de tres términos, dos de los cuales son cuadrados perfectos de las cantidades a y b y están precedidos del mismo signo, mientras que el tercer término es exactamente el doble producto de a y b, pudiendo ser de signo diferente.

Se obtiene un trinomio cuadrado perfecto al elevar al cuadrado la suma o la diferencia de un binomio y algebraicamente, su forma es la siguiente:

a² ± 2∙ab + b²

Como puede verse, el trinomio cuadrado perfecto contiene:

• Dos términos cuadráticos no semejantes precedidos del mismo signo: a² y b²
• Un tercer término 2∙ab, que es el doble producto de las raíces cuadradas de los términos cuadráticos y que puede estar precedido por un signo positivo o negativo.

Los trinomios cuadrados perfectos pueden ser de una o más variables. Por ejemplo, el siguiente trinomio es cuadrado perfecto de una variable:

• x² + 6x + 9

Nótese que los términos primero (x²) y tercero (9) son cuadrados, respectivamente, de las cantidades denominadas a y b. En efecto, x² es el cuadrado de x y 9 es el cuadrado de 3. De esta manera se puede escribir lo siguiente:

a = x

b = 3

Y el término restante es el doble producto de x y de 3:

6x = 2∙3∙x

Una vez hecha la verificación, es seguro que este trinomio es cuadrado perfecto.

Ejemplos

Los trinomios cuadrados perfectos también aparecen en dos o más variables, por ejemplo:

4x² + 4xy + y²

Es un trinomio en dos variables: “x” e “y”. Se puede asegurar que es un trinomio cuadrado perfecto, ya que presenta dos términos cuadráticos:

4x² = (2x)²

y² = (y)²

Y el término restante es el doble producto de las respectivas raíces cuadradas: “2x” y “y”:

4xy = 2∙2x∙y

Los trinomios presentados hasta ahora son de grado 2 en la variable “x”, pero no necesariamente tienen que ser así. El siguiente trinomio es de grado 4 en “x”:

9x⁴ − 30x²yz + 25y²z²

Se verifica fácilmente que este es un trinomio cuadrado perfecto. El primer término es el cuadrado perfecto de 3x², ya que (3x²)² = 9x⁴.

El término 25y²z² es igual a (5yz)². Por último, el término restante es 2∙3x²∙5yz = 30 x²yz.

En cambio, los trinomios que se muestran a continuación no son trinomios cuadrados perfectos:

• x²  + 8x − 16

No es un trinomio cuadrado perfecto debido a que el 16, aunque es 4², está precedido de un signo negativo, mientras que el otro término cuadrático (x²) es positivo.

• x²  − 15x + 25

Tampoco es un trinomio cuadrado perfecto, porque aunque cuenta con dos términos cuadráticos: x² y 5², el término 15x no es igual a 2∙5∙x.

• 4x²  + 10x + 32

Este trinomio no es cuadrado perfecto, ya que solamente contiene un término cuadrático: 4x² = (2x)².

Cuadrado de una suma y cuadrado de una diferencia

Se obtienen trinomios cuadrados perfectos desarrollando dos tipos de productos notables:

• El cuadrado de la suma.
• El cuadrado de la diferencia.

Primero se obtiene el desarrollo a partir de la propiedad distributiva, ya que elevar el binomio al cuadrado significa multiplicarlo consigo mismo:

(a ± b)² = (a ± b) × (a ± b) = a² ± a∙b ± b∙a + b² = a² ± 2a∙b + b²

El trinomio que se obtiene es un resultado que se memoriza con apenas un poco de práctica y es una especie de atajo que facilita el desarrollo, por eso se llama producto notable.

Los siguientes trinomios se obtienen fácilmente mediante el producto notable, sin necesidad de volver a aplicar la propiedad distributiva.

• (x + 6)² = x² + 2∙6∙x + 6² = x² + 12x + 36
• (2x − 10)² = (2x)² − 2∙10∙2x + 10² = 4x² − 40x + 100
• (5y + 2x)² = (5y)² + 2∙5y∙2x + (2x)² = 25y² +20xy + 4x²

Factorización de un trinomio cuadrado perfecto

Una operación frecuente y necesaria en álgebra es la factorización del trinomio cuadrado perfecto, mediante la cual se expresa el trinomio como el cuadrado de una suma o de una resta de dos términos (un binomio).

Es la operación inversa a desarrollar el producto notable, ya que teniendo el trinomio resultante, la idea es obtener el binomio que le da origen cuando se eleva a la 2.

Por ejemplo, en el trinomio cuadrado perfecto previamente analizado 4x² + 4xy + y², ¿Cuál es el binomio que al ser elevado al cuadrado le da origen?

Las respectivas raíces cuadradas de los términos cuadráticos son:

√(4x²) = 2x

Lo cual es equivalente a: 4x² = (2x)²

√(y²) = y

Equivalente a decir que: y² = (y)²

Por lo tanto:

4x² + 4xy + y² = (2x + y)²

¿Y cuál es el binomio que origina al trinomio cuadrado perfecto 9x⁴ − 30x²yz + 25y²z²? Nuevamente se extraen las raíces cuadradas de los términos cuadráticos:

√(9x⁴) = 3x²

√(25y²z²) = 5yz

Entonces:

(3x² − 5yz)² = 9x⁴ − 30x²yz + 25y²z²

Ejercicios resueltos

Ejercicio 1

En cada uno de los siguientes trinomios, completar el espacio en blanco con el término que falta para que sea un trinomio cuadrado perfecto:

a) m² + 18m + _____

b) 4x² − _____ + 64

c) _____ + 30n + 25

• Solución a

Según la fórmula del producto notable:

(a ± b)² =  a² ± 2a∙b + b²

Del trinomio:

m² + 18m + _____

Se deduce que:

a = m     (Para que a² = m²)

Además el término central es: 2∙a∙b = 2m∙b = 18m, por lo tanto b = 9 y su cuadrado es  9² = 81. Guiándose por la fórmula del producto notable, el trinomio queda así:

(m + 9)² =  m² + 18m + 81

• Solución b

En este trinomio:

4x² − _____ + 64

Se pueden conocer a y b:

a = √(4x²) = 2x

b = √64 = 8

Por lo tanto, el término que falta es el doble producto de a y b:

2∙ab = 2∙8∙2x = 32x

Y el trinomio buscado es:

4x² − 32x + 64

• Solución c

En el trinomio:

_____ + 30n + 25

Falta el primer término, pero se conoce que:

b = √25 = 5

Y

2∙ab = 2∙a∙5 = 10a = 30n

Por lo tanto a = 3n y el trinomio buscado es:

9n² + 30n + 25

Ejercicio 2

Comprobar que el siguiente es un trinomio cuadrado perfecto y factorizarlo:

16y² − 24yz + 9z²

• Solución

Primero se comprueba que los términos cuadráticos están precedidos por el mismo signo y enseguida se encuentran las respectivas raíces cuadradas:

a = √(16y²) = 4y

b = √(9z²) = 3z

Luego hay que verificar si el término restante es el doble producto de a y b:

2∙ab = 2∙4y∙3z = 24yz

Si lo es, entonces ya se puede factorizar el trinomio como el cuadrado de una diferencia, ya que el término central está precedido de un signo negativo:

16y² − 24yz + 9z² = (4y − 3z)²

Referencias

1. Jiménez, R. 2008. Álgebra. Prentice Hall.
2. Kate’s Math Lessons. Perfect Square Trinomials. Recuperado de: katesmathlessons.com.
3. Stewart, J. 2006. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
4. Zill, D. 2008. Precálculo con avances de cálculo. 4ta. Edición. McGraw Hill.