Isocuantas e isocostos: concepto, diferencias y ejemplos
¿Qué son las isocuantas e isocostos?
Las isocuantas e isocostos son dos tipos de curvas diferentes que se muestran como representaciones gráficas para que un empresario pueda determinar el método de producción más eficiente para su empresa, es decir, el que tenga el costo total más bajo por unidad producida.
Una isocuanta es una curva en la que las diversas combinaciones de dos factores de producción específicos, como cantidad de mano de obra y de maquinaria, generan una misma cantidad producida. Es decir, es una curva a lo largo de la cual es constante la tasa máxima de producción alcanzable.
También se conocen como curvas de producción constante. Por tanto, una curva isocuanta indica las diversas combinaciones de dos factores de producción que le dan al productor el mismo nivel de producción por unidad de tiempo.
Conociendo la naturaleza de las isocuantas, mediante las líneas de isocostos se pasa a considerar los costos de estos factores.
Una línea de isocosto representa las diferentes combinaciones de dos factores de producción específicos que una empresa puede comprar por el mismo monto de dinero, al costo dado que tenga cada factor.
Diferencias y ejemplos
Un empresario podría utilizar todo su capital únicamente para comprar maquinarias o para pagar el salario del personal. Sin embargo, ninguna de estas situaciones extremas serviría. O nadie operaría las máquinas al no poderse pagar los salarios, o los trabajadores no tendrían las máquinas necesarias para realizar su labor.
Por tanto, el empresario debe combinar de la mejor manera el total de trabajo y de maquinarias, tomando en cuenta el costo que debe pagar por cada uno de estos factores. Para ello traza una línea isocosto.
Una curva isocuanta es una representación gráfica de las diferentes combinaciones de dos factores de producción, como Trabajo (T) y Capital (K), que generan un mismo nivel de producción por unidad de tiempo.
La salida producida por las distintas combinaciones de T y K se puede llamar Q, siendo una función de T y K: Q= f (T, K). La siguiente tabla muestra, con números hipotéticos, siete combinaciones posibles de T y K para producir 60 unidades de producción Q:
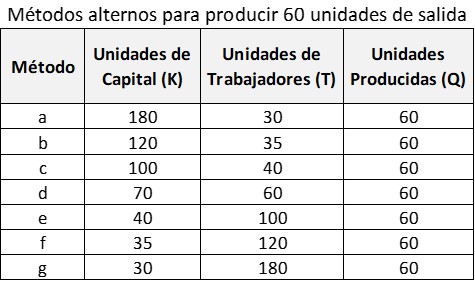
Curva isocuanta
Estas alternativas se muestran en el siguiente gráfico, representada por la curva Q=60. Por tanto, la empresa podría elegir la combinación c: (100K y 40T), la combinación g: (30K y 180T) o cualquier otra combinación indicada en la tabla anterior.
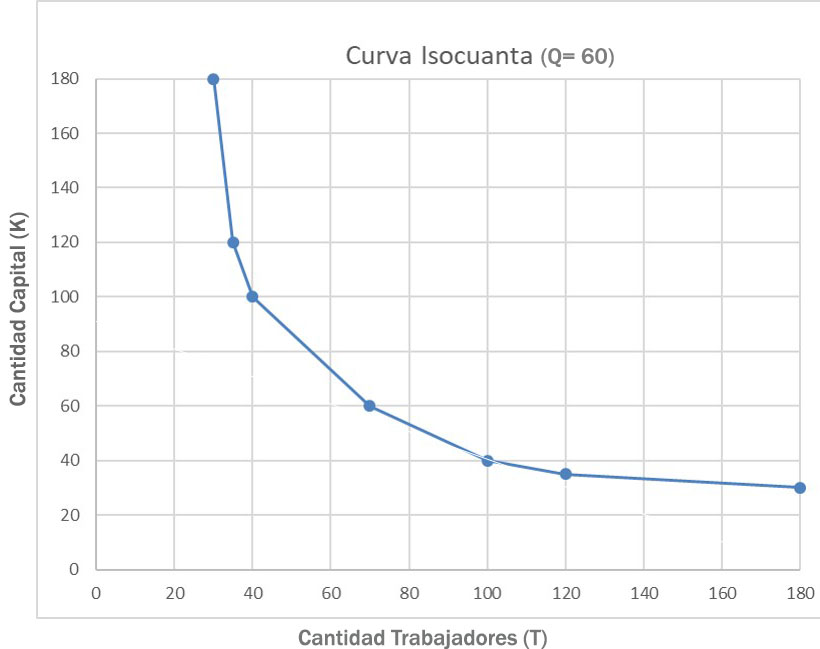
Una isocuanta muestra lo que una empresa quiere producir. Presenta las siguientes propiedades:
La curva es convexa al origen
Esto muestra que la cantidad de capital y de trabajadores pueden reemplazarse entre sí. Sin embargo, el aumento de un factor significa la disminución del otro.
La curva se inclina hacia abajo (tiene pendiente negativa)
Esto indica que solo se puede producir la misma cantidad cuando el incremento de las unidades de un factor de producción se compensa con menos unidades del otro factor. Por ejemplo, una empresa puede obtener el mismo nivel de producción cuando aumenta el recurso de capital, pero disminuyendo el recurso del trabajo.
La curva no debe tocar el eje Y o X del gráfico
De lo contrario, la tasa de reemplazo técnico sería nula, indicando que un factor de producción puede producir la cantidad deseada sin que participe ningún otro factor.
No se pueden cruzar las curvas entre sí
Si se dibujaran varias en un mismo gráfico para mostrar diferentes cantidades deseadas a producir no podrían tocarse entre ellas, porque indicaría que con una combinación de los mismos factores se produciría igual cantidad en ambas, lo que es absurdo por definición.
La forma de la curva es ovalada
Tal como se verá con la línea isocosto, esto es lo que ayuda a estipular la combinación de menor costo de los factores de producción a utilizar.
Línea isocosto
No solo se debe querer producir una cierta cantidad. El empresario debe tener también cierta capacidad para comprar los factores necesarios para alcanzar ese nivel de producción deseado.
Esta capacidad se muestra con su recurso monetario, es decir, cuánto dinero es capaz de gastar en los costos de capital y de trabajo, cuyos precios se toman como constantes. En este caso, el costo del capital viene a ser la tasa de interés bancaria y el del trabajo es el salario del trabajador.
Así, el empresario tiene que operar tomando en cuenta una restricción presupuestaria, que viene representada por la línea de isocosto. Por tanto, para encontrar la combinación de menor costo de los factores para producir las 60 unidades del ejemplo, se necesita construir tal isocosto.
Así, el isocosto es una representación gráfica que muestra las diferentes combinaciones que se pueden adquirir de los factores de producción teniendo un monto determinado de dinero. Por tanto, cada punto en la línea de isocosto representa ese mismo monto.
Cómo se hace
Para delinear esta línea de isocosto se debe haber investigado los precios de mercado de estos dos factores. Por ejemplo, supongamos que el precio del capital es de $40 por unidad y el precio del trabajo es de $20 por unidad.
Así, si el costo unitario de la unidad de trabajo (T) es w=$20 y el costo unitario de la unidad de capital (K) es r=$40, entonces el costo total C= wT + rK.
Por tanto, si se dispone de un monto total C=$3.600, se podrían comprar 90r+0w, 0r+180w u otras combinaciones, como 50r+80w. Todas estas y otras combinaciones se muestran en el siguiente gráfico, mediante la línea de isocosto C= $3.600.
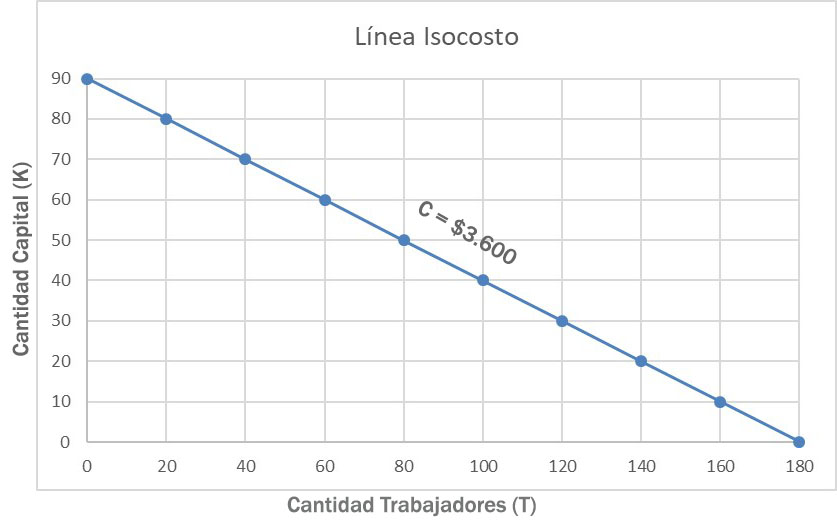
Como no varía el precio de cada factor, el isocosto es una línea recta. Por otro lado, su pendiente es negativa porque representa la relación entre el costo del trabajo y el del capital: w / r. Se conoce como tasa de sustitución de factores, con la cual se puede reemplazar el factor trabajo por el factor capital.
Minimización del costo
La empresa debe buscar minimizar el costo de producir un determinado nivel de producción. Para encontrar la combinación de menor costo de los factores para un nivel fijo de producción, se combina el gráfico de la curva isocuanta con el de la línea isocosto.
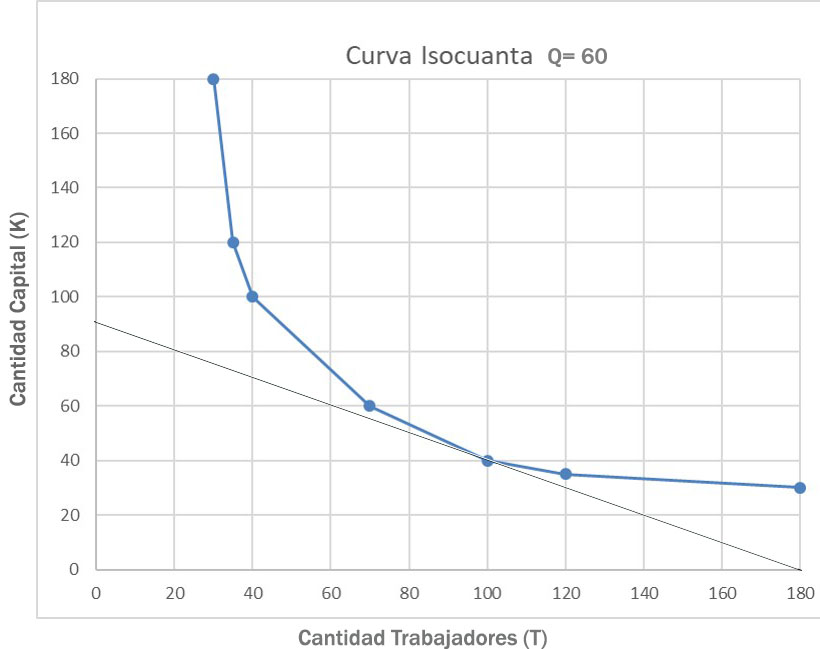
La empresa intentará encontrar la combinación de factores menos costosa a lo largo de su isocuanta. Será la posición de menor costo el punto donde la isocuanta toca tangencialmente, sin cruzarla, la línea de isocosto.
Así, la optimización en la producción se alcanza cuando los precios de los factores y la cantidad a producir sean iguales. Para este ejemplo, el punto de costo mínimo será la combinación “e” de la tabla: K=40 y T=100.
Referencias
- Smriti Chand (2021). Laws of Returns: The Isoquant-Isocost Approach | Economics. Your Article Library. Tomado de: yourarticlelibrary.com.
- Neetescuela (2021). Isocuantas e isocostos. Tomado de: neetescuela.org.
- Will Kenton (2020). Isoquant Curve. Investopedia. Tomado de: investopedia.com.
- Nipun S. (2021). Isoquant and Isocost Lines (With Diagram). Economics Discussion. Tomado de: economicsdiscussion.net.
- Wikieducator (2021). Isoquant and Isocost Itexon. Tomado de: wikieducator.org.
