Ley de Lenz: fórmula, ecuaciones, aplicaciones, ejemplos
La ley de Lenz establece que la polaridad de la fuerza electromotriz inducida en un circuito cerrado, debido a la variación en el flujo de campo magnético, es tal que se opone a la variación de dicho flujo.
El signo negativo que se antepone a la ley de Faraday, toma en consideración la ley de Lenz, siendo el motivo por el que se le denomina ley de Faraday-Lenz y la cual se expresa así:
Índice del artículo
ε representa la fuerza electromotriz inducida, abreviada como fem, Φ es el flujo de campo magnético y t es el tiempo. Las unidades en el Sistema Internacional (SI) para la fem son los voltios (V).
Por su parte el flujo de campo magnético Φ está definido mediante el siguiente producto escalar:
En la ecuación mostrada B es constante y la unidad para Φ en el SI para el flujo de campo magnético es el weber (W):
1 weber = 1 Tesla. metro2
Otra forma de expresar Φ es la que se obtiene al emplear la definición de producto escalar:
Φ = B.A.cos θ
En esta ecuación, B es la magnitud del campo magnético (sin negrita o flecha, para distinguir al vector de su magnitud), A es el área de la superficie atravesada por el campo y θ es el ángulo entre los vectores B y n.
El flujo de campo magnético puede variarse de distintas formas en el tiempo, para crear una fem inducida en una espira –un circuito cerrado- de área A. Por ejemplo:
-Haciendo que el campo magnético sea variable con el tiempo: B = B (t), manteniendo el área y el ángulo constante, entonces:
La aplicación inmediata de la ley de Lenz es determinar el sentido de la fem o corriente inducida sin necesidad de realizar algún cálculo. Considérese lo siguiente: se tiene una espira en medio de un campo magnético, como por ejemplo el que produce un imán de barra.
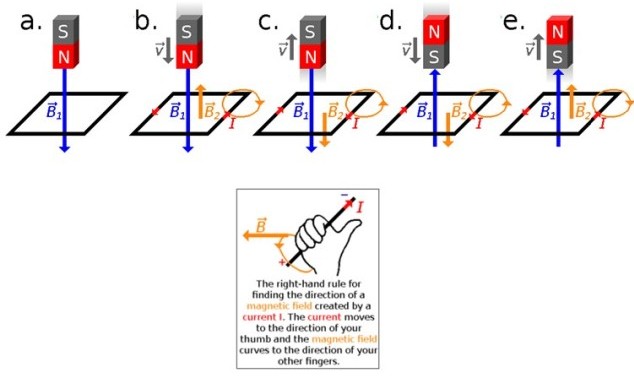
Si el imán y la espira están en reposo uno respecto a la otra no sucede nada, es decir, no habrá corriente inducida, porque el flujo de campo magnético permanece constante en ese caso, (ver figura 2a). Para que se induzca corriente, es preciso que el flujo varíe.
Ahora bien, si se produce un movimiento relativo entre el imán y la espira, ya sea desplazando el imán hacia la espira, o esta hacia el imán, ahí sí habrá corriente inducida para medir (Figura 2b en adelante).
Esta corriente inducida genera a su vez un campo magnético, por lo tanto tendremos dos campos: el del imán B1 en color azul y el que está asociado con la corriente creada por inducción B2, en color naranja.
La regla del pulgar derecho permite conocer la dirección de B2, para ello se coloca el pulgar de la mano derecha en la dirección y sentido que tenga la corriente. Los otros cuatro dedos indican la dirección en que el campo magnético se curva, de acuerdo a la figura 2 (abajo).
Digamos que el imán se deja caer hacia la espira con su polo norte dirigido hacia ella (figura 3). Las líneas de campo del imán salen del polo norte N y entran al polo sur S. Entonces sí habrá cambios en Φ, el flujo creado por B1 que atraviesa la espira: ¡Φ aumenta! Por lo tanto en la espira se crea un campo magnético B2 con intención opuesta.
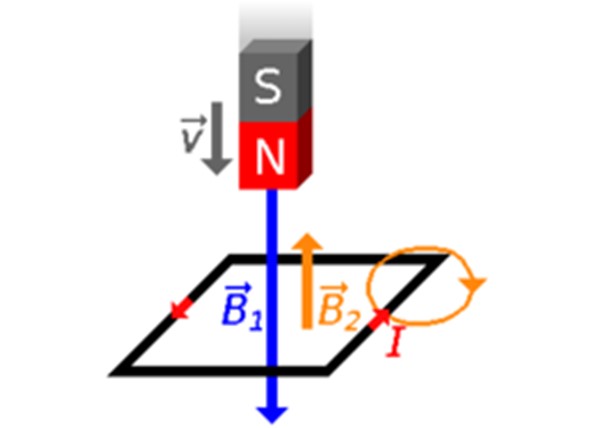
La corriente inducida tiene sentido contrario al de las agujas del reloj, -flechas rojas en las figuras 2 y 3-, según la regla del pulgar derecho.
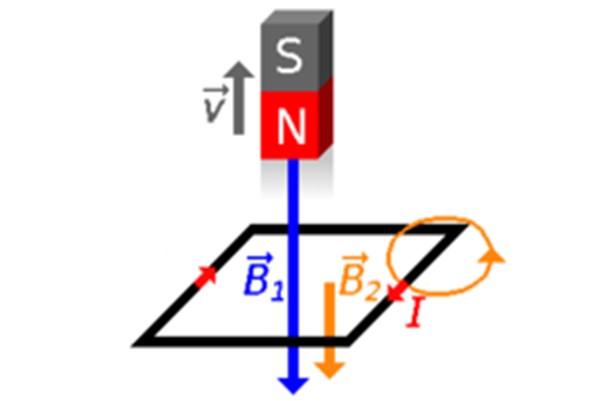
Alejemos el imán de la espira y entonces su Φ disminuye (figuras 2c y 4), por lo tanto la espira se apresura a crear en su interior un campo magnético B2 en el mismo sentido, para compensar. Por lo tanto la corriente inducida es horaria, como se aprecia en la figura 4.
Invirtiendo la posición del imán
¿Qué ocurre si se invierte la posición del imán? Si el polo sur apunta hacia la espira, el campo apunta hacia arriba, ya que las líneas de B en un imán salen del polo norte y entran al polo sur (ver figura 2d).
De inmediato la ley de Lenz informa que este campo vertical hacia arriba, precipitándose hacia la espira, inducirá en esta un campo contrario, es decir, B2 hacia abajo y la corriente inducida también será horaria.
Finalmente se aleja al imán de la espira, siempre con su polo sur apuntando hacia el interior de esta. Entonces en el interior de la espira se produce un campo B2 para contribuir a que el alejamiento del imán no cambie el flujo de campo en ella. Tanto B1 como B2 tendrán el mismo sentido (ver figura 2d).
El lector se dará cuenta de que, tal como prometimos, no se han realizado cálculos para saber el sentido de la corriente inducida.
Heinrich Lenz (1804-1865) realizó numerosos trabajos experimentales a lo largo de su carrera científica. Los más conocidos son los que acabamos de describir, dedicándose a medir las fuerzas y los efectos magnéticos creados al dejar caer abruptamente un imán en medio de una espira. Con sus resultados refinó los trabajos realizados por Michael Faraday.
Ese signo negativo en la ley de Faraday resulta ser el experimento por el cual más se le reconoce hoy en día. No obstante, Lenz realizó muchos trabajos en Geofísica durante su juventud y entretanto se dedicaba a dejar caer imanes dentro de las espiras y tubos. También hizo estudios acerca de la resistencia eléctrica y la conductividad de los metales.
En particular, sobre los efectos que tiene el aumento de temperatura en el valor de la resistencia. No dejó de observar que al calentar un alambre, la resistencia disminuye y se disipa calor, algo que también James Joule observó de manera independiente.
Para recordar por siempre sus aportes al electromagnetismo, además de la ley que lleva su nombre, a las inductancias (bobinas) se las denota con la letra L.
Es un experimento en el que se demuestra como un imán se frena cuando es liberado dentro de un tubo de cobre. El imán al caer, va generando variaciones en el flujo de campo magnético dentro del tubo, al igual que sucede con la espira de corriente.
Entonces se crea una corriente inducida que se opone al cambio en el flujo. El tubo crea su propio campo magnético para esto, el cual como ya sabemos, está asociado a la corriente inducida. Supongamos que el imán se suelta con el polo sur hacia abajo, (figuras 2d y 5).

Como resultado, el tubo crea un campo magnético propio con un polo norte hacia abajo y un polo sur hacia arriba, que es equivalente a crear un par de imanes ficticios, uno por encima y otro por debajo del que está cayendo.
El concepto queda plasmado en la siguiente figura, pero es necesario recordar que los polos magnéticos son inseparables. Si el imán ficticio inferior tiene un polo norte hacia abajo, irá acompañado necesariamente de un sur hacia arriba.
Como los polos opuestos se atraen y los contrarios se repelen, el imán que cae se verá repelido, y a la vez atraído por el imán ficticio superior.
El efecto neto siempre será de frenado aunque el imán se suelte con el polo norte hacia abajo.
La ley Joule-Lenz describe como parte de la energía asociada a la corriente eléctrica que circula por un conductor se pierde en forma de calor, un efecto que se aprovecha en los calentadores eléctricos, las planchas, los secadores de cabello y las hornillas eléctricas, entre otros electrodomésticos.
Todos ellos tienen una resistencia, filamento o elemento calefactor que se calienta al paso de la corriente.
En forma matemática, sea R la resistencia del elemento calefactor, I la intensidad de corriente que circula por él y t el tiempo, la cantidad de calor producida por efecto Joule es:
Q = I2. R. t
Donde Q se mide en joules (unidades SI). James Joule y Heinrich Lenz descubrieron este efecto simultáneamente alrededor de 1842.
A continuación mostramos tres ejemplos importantes en los que se aplica la ley de Faraday-Lenz:
Un generador de corriente alterna transforma energía mecánica en energía eléctrica. El fundamento se describió al comienzo: una espira se hace girar en medio de un campo magnético uniforme, como el que se crea entre los dos polos de un gran electroimán. Cuando se usan N espiras, la fem aumenta proporcionalmente a N.
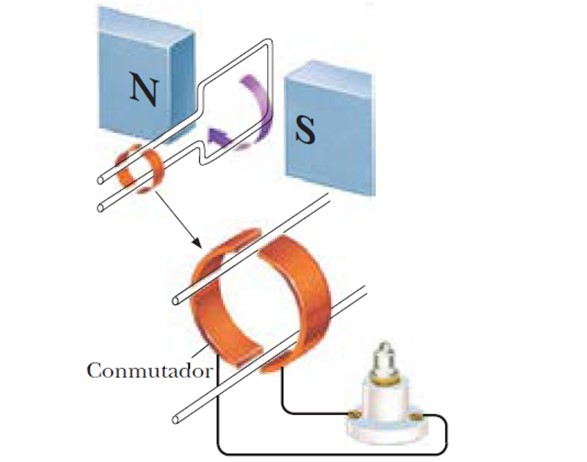
A medida que la espira da vueltas, el vector normal a su superficie cambia su orientación respecto al campo, produciendo una fem que varía de forma sinusoidal con el tiempo. Supongamos que la frecuencia angular de rotación es ω, entonces al sustituir en la ecuación que se dio al principio, se tendrá:
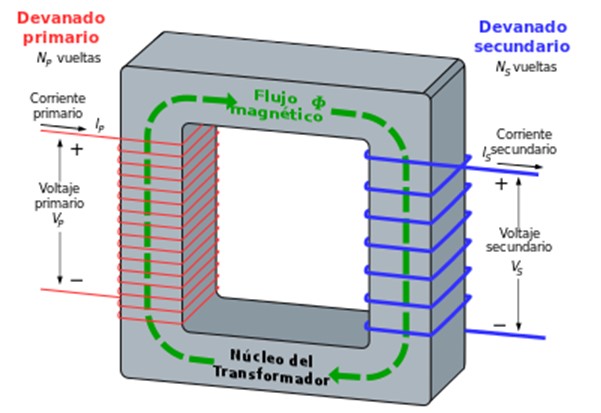
Es un dispositivo que permite obtener un voltaje directo a partir de un voltaje alterno. El transformador forma parte de innumerables dispositivos, como el cargador de un teléfono celular, por ejemplo.Funciona de la siguiente manera:
Se tienen dos bobinas enrolladas alrededor de un núcleo de hierro, una se denomina primaria y la otra secundaria. El número de vueltas respectivo es N1 y N2.
La bobina o devanado primario se conecta a un voltaje alterno (como la toma de electricidad casera, por ejemplo) de la forma VP =V1.cos ωt, haciendo que en su interior circule una corriente alterna de frecuencia ω.
Esta corriente origina un campo magnético que a su vez causa un flujo magnético oscilante en la segunda bobina o devanado, con un voltaje secundario de la forma VS = V2.cos ωt.
Ahora bien, resulta que el campo magnético en el interior del núcleo de hierro es proporcional al inverso del número de vueltas del devanado primario:
B ∝ 1 /N1
Y así también lo será VP, el voltaje en el devanado primario, mientras que la fem inducida VS en el segundo devanado es proporcional, como ya sabemos, al número de vueltas N2 y también a VP.
Así que combinando estas proporcionalidades se tiene una relación entre VS y VP que depende del cociente entre el número de espiras de cada uno, de la siguiente forma:
VS = (N2 /N1) VP
Son dispositivos utilizados en los bancos y los aeropuertos para seguridad. Detectan la presencia de cualquier metal, no solamente hierro o níquel. Ellos funcionan gracias a las corrientes inducidas, mediante el uso de dos bobinas: una transmisora y otra receptora.
Se hace pasar una corriente alterna de alta frecuencia en la bobina transmisora, para que genere un campo magnético alterno a lo largo del eje (ver figura), el cual induce una corriente en la bobina receptora, algo más o menos parecido a lo que ocurre con el transformador.
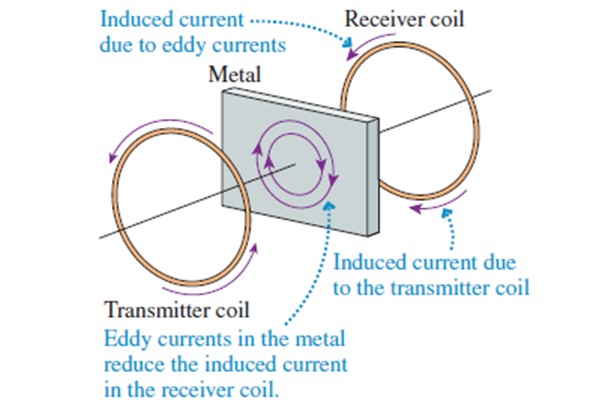
Si un pedazo de metal se coloca entre ambas bobinas, aparecen en él unas pequeñas corrientes inducidas, llamadas corrientes de Foucault (que no pueden fluir en un aislante). La bobina receptora responde ante los campos magnéticos de la bobina transmisora y los que se crean por las corrientes de Foucault.
Las corrientes de Foucault intentan minimizar el flujo de campo magnético en el trozo de metal. Por lo tanto el campo que percibe la bobina receptora, disminuye al interponer una pieza metálica entre ambas bobinas. Cuando esto sucede se dispara una alarma que avisa la presencia de un metal.
Se tiene una bobina circular con 250 espiras de 5 cm de radio, ubicada perpendicularmente a un campo magnético de 0.2 T. Determinar la fem inducida si en un intervalo de tiempo de 0.1 s, la magnitud del campo magnético se duplica y señalar el sentido de la corriente, conforme a la siguiente figura:

Solución
Primero calcularemos la magnitud de la fem inducida, luego se indicará el sentido de la corriente asociada de acuerdo al dibujo.
N= 250 vueltas
A = π. R2 = p . (5 x 10-2 m)2 = 0.0079 m2.
cos θ = cos 0 = 1 (El vector n se toma paralelo a B)
Como el campo magnético duplica su magnitud, se tiene:
Sustituyendo estos valores en la ecuación para la magnitud de la fem inducida:
ε = 250. 0.0079 m2 . 2 T/s = 3.95 V
Puesto que el campo se ha duplicado, también lo ha hecho el flujo de campo magnético, por lo tanto en la espira se crea una corriente inducida que se opone a dicho aumento.
El campo de la figura apunta hacia dentro de la pantalla. El campo creado por la corriente inducida debe salir de la pantalla, aplicando la regla del pulgar derecho, se deduce que la corriente inducida es antihoraria.
Un devanado cuadrado está formado por 40 espiras de 5 cm de lado, que gira con frecuencia de 50 Hz en medio de un campo uniforme de magnitud 0.1 T. Inicialmente la bobina se encuentra perpendicular al campo. ¿Cuál será la expresión para la fem inducida?
Solución
De apartados anteriores se dedujo esta expresión:
ε = N.B.A. ω. sen ωt
A = (5 x 10-2 m)2 = 0.0025 m2
N = 40 espiras
ω= 2π.f = 2π.50 Hz = 100p s-1
B = 0.1 T
ε = 40 x 0.1 x 0.0025 x 100π x sen 50.t =p . sen 100π.t V
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 6. Electromagnetismo. Editado por Douglas Figueroa (USB).
- Hewitt, Paul. 2012. Conceptual Physical Science. 5th. Ed. Pearson.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- OpenStax College. Faraday’s Law of Induction: Lenz’s Law. Recuperado de: opentextbc.ca.
- Physics Libretexts. Lenz’s Law. Recuperado de: phys.libretexts.org.
- Sears, F. (2009). Física Universitaria Vol. 2.
