Método axiomático: qué es, características, pasos, ejemplos

¿Qué es el método axiomático?

El método axiomático es un procedimiento formal utilizado por las ciencias mediante el cual se formulan enunciados o proposiciones denominados axiomas, conectados entre sí por una relación de deductibilidad y que son la base de las hipótesis o condiciones de un cierto sistema.

Esta definición general debe enmarcarse dentro de la evolución que esta metodología ha tenido a lo largo de la historia. En primer lugar, existe un método antiguo o de contenido, nacido en la Antigua Grecia a partir de  Euclides y desarrollado luego, por Aristóteles.

En segundo lugar, ya en el siglo XIX, la aparición de una geometría con axiomas distintos de los de Euclides. Y por último, el método axiomático formal o moderno, cuyo máximo exponente fue David Hilbert.

Más allá de su desarrollo a lo largo del tiempo, este procedimiento ha sido la base del método deductivo utilizándose en la geometría y la lógica donde se originó. También se ha empleado en la física, la química y la biología.

Y hasta se ha llegado a aplicar dentro de la ciencia jurídica, la sociología y la economía política. No obstante, actualmente su esfera de aplicación más importante es  las matemáticas y la lógica simbólica y algunas ramas de la física como la termodinámica, la mecánica, entre otras disciplinas.

Características del método axiomático

Si bien la característica fundamental de este método es la formulación de axiomas, estos no han sido siempre considerados de la misma manera.

Existen algunos que se pueden definir y construir de un modo arbitrario. Y otros, según un modelo en el que se considere su verdad garantizada intuitivamente.

Para poder comprender específicamente en qué consiste esta diferencia y sus consecuencias, es necesario recorrer la evolución de este método.

Método axiomático antiguo o de contenido 

Es el establecido en la Antigua Grecia hacia el siglo V a.C. Su esfera de aplicación es la geometría. La obra fundamental de esta etapa son los Elementos de Euclides, aunque se considera que antes que él, Pitágoras, ya había dado nacimiento al método axiomático.

Así los griegos toman ciertos hechos como axiomas, sin que se necesite ninguna prueba lógica,  es decir, sin necesidad de demostración, ya que para ellos son una verdad evidente por sí misma.

Por su parte Euclides presenta cinco axiomas para la geometría:

1. Dados dos puntos existe una recta que los contiene o los une.
2. Cualquier segmento se puede prolongar continuadamente en una recta ilimitada por ambos lados.
3. Se puede trazar una circunferencia que posea un centro en cualquier punto y un radio cualquiera.
4. Los ángulos rectos son todos iguales.
5. Tomando cualquier línea recta y cualquier punto que no se encuentre en ella, existe una línea recta paralela a aquella y que contiene a ese punto. Este axioma es conocido, después, como el axioma de las paralelas y ha sido enunciado también como: por un punto exterior a una recta se puede trazar una única paralela.

Sin embargo, tanto Euclides como matemáticos posteriores, coinciden en que el quinto axioma no es tan claro intuitivamente como los otros 4. Inclusive durante el Renacimiento se intenta deducir el quinto de los otros 4, pero no es posible.

Esto hizo que ya en el siglo XIX, quienes mantuvieran los cinco fueran partidarios de la geometría euclidiana y los que negaron el quinto, fueran quienes crearon las geometrías no euclidianas.

Método axiomático no euclidiano

Son precisamente Nikolái Ivánovich Lobachevski, János Bolyai y Johann Karl Friedrich Gauss quienes ven la posibilidad de construir, sin contradicción, una geometría que provenga de sistemas de axiomas distintos de los de Euclides. Esto destruye la creencia en la verdad absoluta o a priori de los axiomas y las teorías que derivan de ellos.

Por consiguiente, los axiomas comienzan a concebirse como puntos de partida de una teoría determinada. También tanto su elección como el problema de su validez en uno u otro sentido, comienzan a relacionarse con hechos fuera de la teoría axiomática.

De este modo aparecen teorías geométricas, algebraicas y aritméticas construidas por  medio del método axiomático.

Esta etapa culmina con la creación de sistemas axiomáticos para la aritmética como el de Giuseppe Peano en 1891; la geometría de David Hubert en 1899; los enunciados y cálculos de predicados de Alfred North Whitehead y Bertrand Russell, en Inglaterra en 1910; la teoría axiomática de los conjuntos de Ernst Friedrich Ferdinand Zermelo en 1908.

Método axiomático moderno o formal

Es David Hubert quien inicia la concepción de un método axiomático formal y que lleva a su culminación, David Hilbert.

Es precisamente Hilbert quien formaliza el lenguaje científico, considerando a sus enunciados como fórmulas o secuencias de signos que no tienen en sí mismos ningún significado. Solo adquieren significado en una determinada interpretación.

En “Los fundamentos de la geometría” explicita el primer ejemplo de esta metodología. A partir de aquí la geometría se convierte en una ciencia de consecuencias lógicas puras, que se extraen de un sistema de hipótesis o axiomas, mejor articulado que el sistema euclidiano.

Esto es porque en el sistema antiguo la teoría axiomática se funda en la evidencia de los axiomas. En tanto en la fundamentación de la teoría formal se da por la demostración de la no contradicción de sus axiomas.

Pasos del método axiomático

El procedimiento que lleva adelante una estructuración axiomática dentro de las teorías científicas reconoce:

• A-La elección de cierta cantidad de axiomas, o sea una cantidad de proposiciones de una cierta teoría que se aceptan sin necesidad de ser demostradas.
• B-Los conceptos que forman parte de dichas proposiciones no se determinan dentro del marco de la teoría dada.
• C-Las reglas de definición y de deducción de la teoría dada se fijan y permiten introducir nuevos conceptos dentro de la teoría y deducir lógicamente unas proposiciones de otras.
• D-Las demás proposiciones de la teoría, o sea el teorema, se deducen de A sobre la base de C.

Ejemplos

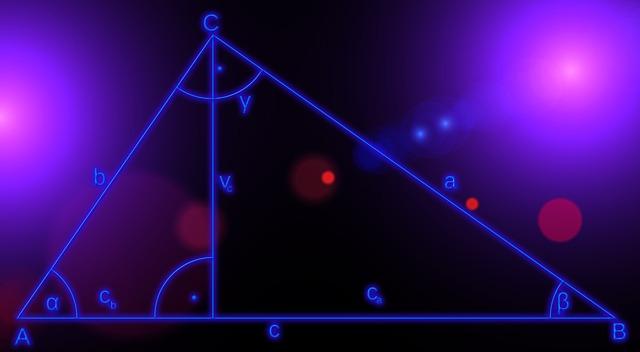
Este método puede verificarse a través de la  demostración de los dos teoremas de Euclides más conocidos: el teorema de los catetos y el de la altura.

Ambos surgen de la observación de este geómetra griego de que cuando se traza la altura con respecto a la hipotenusa dentro de un triángulo rectángulo aparecen dos triángulos más del original. Dichos triángulos son semejantes entre sí y a la vez semejantes con el triángulo de origen. Esto supone que sus lados respectivos homólogos son proporcionales.

Se  puede observar que los ángulos congruentes en los triángulos de esta forma verifican la semejanza que existe entre los tres triángulos implicados de acuerdo con el criterio de semejanza AAA. Este criterio sostiene que cuando dos triángulos tienen todos sus ángulos iguales son semejantes.

Una vez que se demuestra que los triángulos son semejantes se pueden establecer las proporciones que se especifican en el primer teorema. El mismo enuncia que en un triángulo rectángulo, la medida de cada cateto es media proporcional geométrica entre la hipotenusa y la proyección del cateto en ella.

El segundo teorema es el de la altura. En él se especifica que cualquier triángulo rectángulo la altura que se traza de acuerdo a la hipotenusa es media proporcional geométrica entre los segmentos que quedan determinados por dicha media geométrica sobre la hipotenusa.

Por supuesto que ambos teoremas tienen numerosas aplicaciones en todo el mundo no solamente en el ámbito de la enseñanza, sino también en la ingeniería, física, química y astronomía.