Valor absoluto: propiedades, ejemplos, ejercicios

¿Qué es el valor absoluto?

El valor absoluto de un número real se define como la distancia que hay entre ese número y el 0 de la recta real. Por ser una distancia, su valor es siempre positivo o cero e igual a la figura del número.

El valor absoluto se representa ubicando el número entre dos barras verticales, símbolo que se lee: “valor absoluto de”, tal como se resume en el siguiente cuadro:

Por ejemplo, el valor absoluto de -3 se escribe como │-3│ y es igual a 3. Esto significa que entre el -3 y el 0 hay tres unidades, que representa los números sobre la recta real. Por su parte el valor absoluto de +3 o simplemente 3, también es igual a 3, ya que al medir su distancia al 0 también es de tres unidades.

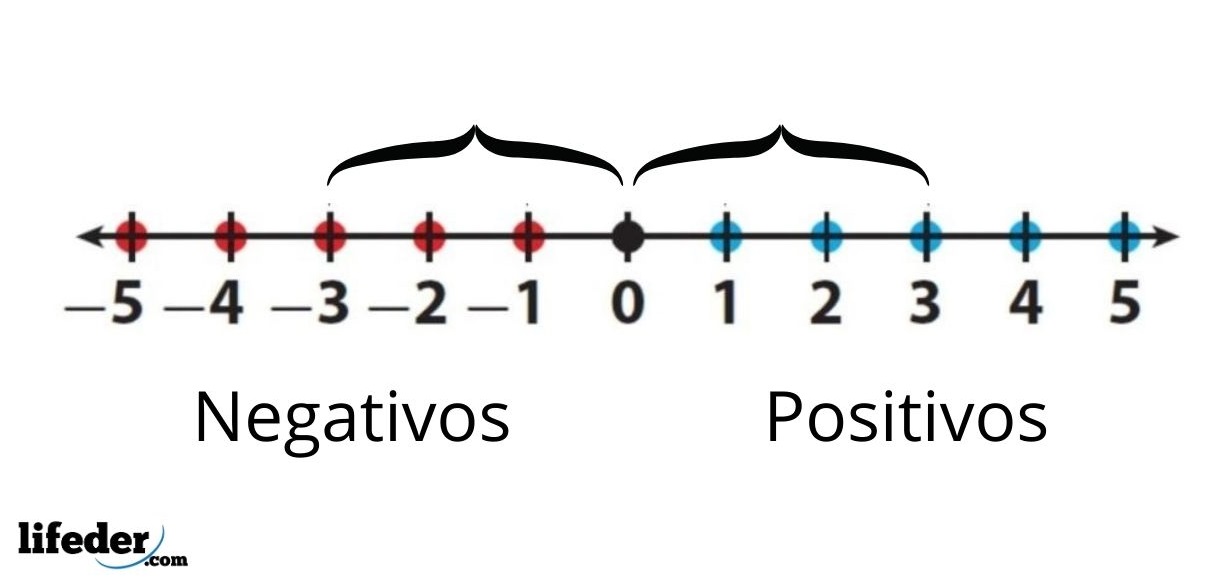
En resumen, el valor absoluto de un número es la misma figura del número pero siempre con signo positivo.

Propiedades del valor absoluto

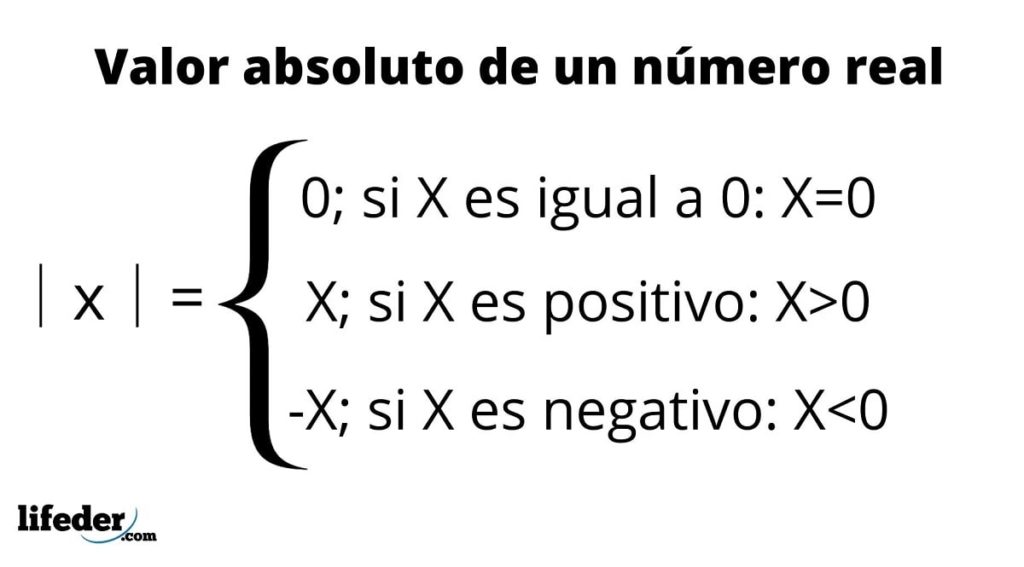
A continuación las principales propiedades del valor absoluto:

• 1) El valor absoluto de un número siempre es positivo o 0, por lo tanto:

│x│≥ 0

• 2) El valor absoluto de cero también es cero, es decir │0│ = 0, por lo tanto se puede afirmar que:

│x│ = 0, si y solo si x = 0

• 3) Para todo número x que pertenece al conjunto de los números reales, el valor absoluto de x es igual al valor absoluto de – x:

│x│=│−x│

• 4) Si el valor absoluto de un número x es a, significa que hay dos opciones para ese número: i) x = +a o ii) x = -a.

Por ejemplo, si el valor absoluto de un número es 5, las dos posibilidades son que el número sea +5 o -5.

Operaciones con valor absoluto

Las siguientes propiedades son muy útiles para hacer operaciones con valores absolutos:

• 5) Para “x” e “y” que son dos números reales, se cumple siempre la siguiente desigualdad, llamada desigualdad triangular del valor absoluto:

│x│+│y│≥ │x+y│

Por ejemplo, sean:

x = -6

y = 9

El lado izquierdo de la desigualdad es:

│-6│+│9│= 6 + 9 =16

Y el lado derecho es:

│-6+9│=│3│=3

Evidentemente 16 es mayor o igual que 3, y siempre sucede así cuando los números x e y tienen signos diferentes. Si tienen signos iguales, entonces se obtiene la igualdad. Véase este otro ejemplo con otros dos valores diferentes:

x = -5

y = -3

│-5│+│-3│≥ │-5-3│

5+3≥│-8│

Efectivamente:

8 = 8

• 6) El producto de los respectivos valores absolutos de dos número reales “x” e “y” es igual al valor absoluto del producto de los números:

│x│∙│y│= │x∙y│

Nuevamente sean los valores:

x = -6

y = 9

Entonces:

│-6│∙│9│= 6∙9 = 54

Que es igual a:

│(-6)∙9│= │-54│=54

• 7) El cociente del valor absoluto de dos números reales “x” e “y”, con el denominador diferente de 0, es el valor absoluto del cociente entre dichos números:

Siempre y cuando y≠0.

Ejemplo:

Ejemplos de valor absoluto

Ejemplos sencillos

Calcular el valor absoluto de cualquier número real es muy sencillo, por ejemplo el valor absoluto de los siguientes números es:

a) │-14│=14

b) │-(-5)│= │5│=5

c) │π│=π

Cálculos con el valor absoluto de un número real

Realizar las siguientes operaciones que involucran el valor absoluto:

a) 2⋅│8│ + 5⋅│-16│-⋅│4│ = (2⋅8) + (5⋅16) – 4 = 16 + 80 – 4= 92

b) │5-(8⋅3)│– 6 + │81÷(-3)│ 

Esta es una operación combinada, por lo que es preferible resolverla por pasos. El primer valor absoluto es:

│5-(8⋅3)│ = │5-24│= │-19│= 19

El segundo valor absoluto que aparece se calcula así:

│81÷(-3)│= │-27│=27

Luego se reúnen los resultados obtenidos y se lleva a cabo el cálculo final:

│5-(8⋅3)│– 6 + │81÷(-3)│ = 19 – 6 + 27 = 40

La distancia entre dos puntos sobre la recta real

El valor absoluto aparece en muchas aplicaciones, como por ejemplo hallar la distancia entre dos números que pertenecen a la recta real. Si a es un número real entonces se ubica sobre la recta real en el punto cuya abscisa es “a”, igual sucede con un número real b.

Sean “a” y “b” dos números sobre la recta real, la distancia que los separa es:

d_ab =│b−a│

La cual se puede calcular igualmente mediante:

d_ab =│a−b│

Por ejemplo, la distancia entre a = 5 y b = 12 es:

d =│5−12│=│12−5│ = 7

De esta forma, el valor absoluto de la resta entre dos números reales es simplemente la distancia que los separa sobre la recta real.

Función valor absoluto

La función valor absoluto es una aplicación que va del conjunto de los números reales ℛ hasta ℛ⁺, que hace corresponder a cada número real su valor absoluto. Se define mediante:

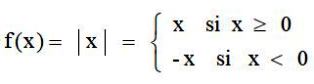
Y su gráfica tiene la típica forma de V:

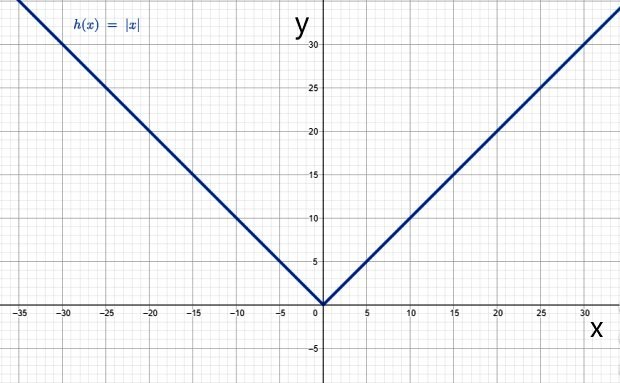
Características de la función valor absoluto

-Su dominio es el conjunto de todos los números reales.

-Es continua.

-Es par, ya que se cumple que f(x) = f(–x), por lo tanto el eje vertical es un eje de simetría.

-El rango de la función valor absoluto es el conjunto de los reales positivos incluyendo al 0, ya que la función siempre representa una distancia, y esta siempre es positiva o nula.

-Es una función por tramos o por partes.

-Decrece en el intervalo (-∞,0) y crece en (0,+∞).

El argumento del valor absoluto también puede ser una función cuadrática o de otro tipo, por ejemplo se puede definir:

• f(x) = │x²-5x+3│
• g(x) = │sen x│

El valor absoluto se encarga de convertir en positivas las imágenes del argumento que tienen signo negativo.

Ejercicios resueltos

Ejercicio 1

Evaluar las siguientes expresiones algebraicas con valor absoluto:

a) │2x−5│ + │−x+1│  en x = 3

b) │(x−5)÷(x+4)│ en x = −1

Solución a

│2⋅3−5│ + │−3+1│=│6−5│ + │−2│=│1│+2 = 3

Solución b

│(−1−5)÷(−1+4)│= │(−6)÷(3)│=│−2│=2

Ejercicio 2

¿Cuál es el conjunto de valores que representa la siguiente desigualdad?

│x│≤ 3

Solución

La desigualdad representa todos los números reales cuyo valor absoluto es menor o igual que 3, por lo tanto es el conjunto de todos los números comprendidos entre –3 y +3, incluyendo a estos.

En la notación de intervalo queda:

[–3,3]

Ejercicio 3

Resolver la siguiente ecuación con valor absoluto:

│2x-1│= 5

Solución 

Como se indicó previamente, para resolver una ecuación con valor absoluto es necesario considerar las dos opciones. Es decir, si:

│f(x)│= c

Entonces:

1) f(x) = c

2) f(x) = -c

Por lo tanto esta ecuación, cuyo argumento es lineal, tiene dos soluciones:

Primera solución

2x – 1 = 5

2x = 6 ⇒ x₁ = 3

Segunda solución

2x – 1 = -5

2x = -4 ⇒ x₂ = -2

Al evaluar x₁ = 3 o x₂ = -2 en la ecuación original se debe obtener una igualdad, de esta forma se comprueba que los valores obtenidos son solución de la ecuación propuesta. En  efecto:

│(2⋅3)-1│= │6-1│=5

Y al probar con la segunda opción, también se obtiene una igualdad:

│2⋅(-2)-1│= │-4-1│=5

Referencias

1. Baldor, A. 2005. Álgebra. Grupo Patria Cultural.
2. Larson, R. 2012. Precálculo. 8va. Edición. Cengage Learning.
3. Hoffman, J. Selección de temas de Matemática. Volumen 2.
4. Stewart, J. 2007. Precálculo: Matemáticas para el cálculo. 5ta. Edición. Cengage Learning.
5. Zill, D. 1984. Álgebra y Trigonometría. McGraw Hill.