Propiedad de cerradura del álgebra: demostración, ejemplos
La propiedad de cerradura del álgebra es un fenómeno que relaciona dos elementos de un conjunto con una operación, donde la condición necesaria es que, después de ser procesados los 2 elementos bajo dicha operación, el resultado también pertenezca al conjunto inicial.
Por ejemplo, si se toman los números pares como conjunto y una suma como operación, se obtiene una cerradura de dicho conjunto con respecto a la suma. Esto es debido a que la suma de 2 números pares siempre arrojará como resultado otro número par, cumpliéndose así la condición de cerradura.

Índice del artículo
- 1 Características
- 2 Álgebra numérica
- 3 Demostración
- 4 Casos especiales en R
- 5 Ejemplos
- 6 Ejercicios propuestos
- 7 Referencias
Son muchas las propiedades que determinan los espacios o cuerpos algebraicos, como estructuras o anillos. Sin embargo, la propiedad de cerradura es una de las más conocidas dentro del álgebra básica.
No todas las aplicaciones de estas propiedades se dan en base a fenómenos o elementos numéricos. Muchos ejemplos cotidianos se pueden trabajar desde un enfoque algebraico-teórico puro.
Un ejemplo puede ser los ciudadanos de un país que asumen una relación legal de cualquier tipo, como sociedad comercial o matrimonio entre otros. Después de realizada esta operación o gestión, siguen siendo ciudadanos del país. De ese modo la ciudadanía y las operaciones de gestión con respecto a dos ciudadanos representan una cerradura.
Con respecto a los números, existen muchos aspectos que han sido motivo de estudio en diferentes corrientes de la matemática y el álgebra. De estos estudios han surgido gran cantidad de axiomas y teoremas que sirven como base teórica de las investigaciones y trabajos contemporáneos.
Si se trabaja con los conjuntos numéricos podemos establecer otra definición válida para la propiedad de cerradura. Se dice que un conjunto A es la cerradura de otro conjunto B si A es el conjunto más pequeño que contiene a todos los conjuntos y operaciones que alberga B.
Se aplica la demostración de cerradura para elementos y operaciones presentes en el conjunto de los números reales R.
Sean A y B dos números que pertenecen al conjunto R, se define la cerradura de estos elementos para cada operación contenida en R.
– Suma: ∀ A ˄ B ∈ R → A + B = C ∈ R
Esta es la manera algebraica de decir que Para todo A y B que pertenece a los números reales, se tiene que la suma de A más B es igual a C, que también pertenece a los reales.
Resulta sencillo comprobar si esta proposición es cierta; basta con efectuar la suma entre cualquier número real y verificar si el resultado pertenece también a los números reales.
3 + 2 = 5 ∈ R
-2 + (-7) = -9 ∈ R
-3 + 1/3 = -8/3 ∈ R
5/2 + (-2/3) = 11/6 ∈ R
Se observa que la condición de cerradura se cumple para los números reales y la suma. De esta manera se puede concluir: La suma de números reales es una cerradura algebraica.
– Multiplicación: ∀ A ˄ B ∈ R → A . B = C ∈ R
Para todo A y B que pertenece a los reales, se tiene que la multiplicación de A por B es igual a C, que también pertenece a los reales.
Al verificar con los mismos elementos del ejemplo anterior se observan los siguientes resultados.
3 x 2 = 6 ∈ R
-2 x (-7) = 14 ∈ R
-3 x 1/3 = -1 ∈ R
5/2 x (-2/3) = -5/3 ∈ R
Esto es suficiente evidencia para concluir que: La multiplicación de números reales es una cerradura algebraica.
Se puede extender esta definición a todas las operaciones de los números reales, aunque encontraremos ciertas excepciones.

Como primer caso especial se observa la división, donde se aprecia la siguiente excepción:
∀ A ˄ B ∈ R → A / B ∉ R ↔ B = 0
Para todo A y B que pertenecen a R se tiene que A entre B no pertenece a los reales si y solo si B es igual a cero.
Este caso se refiere a la restricción de no poder dividir entre cero. Debido a que cero pertenece a los números reales, entonces se concluye que: la división no es una cerradura en los reales.
También existen las operaciones de potenciación, más específicamente las de radicación, donde se presentan excepciones para las potencias radicales de índice par:
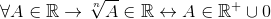
Para todo A que pertenece a los reales se tiene que la raíz enésima de A pertenece a los reales, si y solo si A pertenece a los reales positivos unido a un conjunto cuyo único elemento es cero.
De esta forma se denota que las raíces pares solo se aplican para los reales positivos y se concluye que la potenciación no es una cerradura en R.
De manera homologa se aprecia para la función logarítmica, la cual no se encuentra definida para valores menores o iguales a cero. Para comprobar si el logaritmo es una cerradura de R se procede de la siguiente manera:
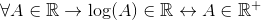
Para todo A que pertenece a los reales se tiene que el logaritmo de A pertenece a los reales, si y solo si A pertenece a los reales positivos.
Al excluirse los valores negativos y el cero que también pertenecen a R se puede afirmar que:
El logaritmo no es una cerradura de los números reales.
Comprobar la cerradura para la suma y la resta de los números naturales:
Lo primero es chequear la condición de cerradura para distintos elementos del conjunto dado, donde si se observa que algún elemento rompe con la condición se puede negar automáticamente la existencia de cerradura.
Esta propiedad se cumple para todos los valores posibles de A y B, como se observa en las siguientes operaciones:
1 + 3 = 4 ∈ N
5 + 7 = 12 ∈ N
1000 + 10000 = 11000 ∈ N
No existen valores naturales que rompan la condición de cerradura, por lo que se concluye:
La suma es una cerradura en N.
Se buscan elementos naturales capaces de romper con la condición; A – B pertenece a los naturales.
Operando es sencillo dar con pares de elementos naturales que no cumplan con la condición de cerradura. Como por ejemplo:
7 – 10 = -3 ∉ a N
De esa forma podemos concluir que:
La resta no es una cerradura del conjunto de los números naturales.
1-Demuestre si se cumple la propiedad de cerradura para el conjunto de los números racionales Q, para las operaciones suma, resta, multiplicación y división.
2-Explique si el conjunto de los números reales es una cerradura del conjunto de los números enteros.
3-Determine qué conjunto numérico puede ser cerradura de los números reales.
4-Demuestre la propiedad de cerradura para el conjunto de los números imaginarios, respecto a la suma, resta, multiplicación y división.
- Panorama de las matemáticas puras: la elección bourbakista. Jean Dieudonné. Reverte, 1987.
- Teoria de numeros algebraicos. Alejandro J. Díaz Barriga, Ana Irene Ramírez, Francisco Tomás. Universidad Nacional Autonoma de Mexico, 1975.
- Álgebra Lineal y sus Aplicaciones. Sandra Ibeth Ochoa García, Eduardo Gutiérrez González.
- Estructuras algebraicas V: teoría de cuerpos. Héctor A. Merklen. Organización de los Estados Americanos, Secretaría General, 1979.
- Introducción al álgebra conmutativa. Michael Francis Atiyah, I. G. MacDonald. Reverte, 1973.
