Aceleración instantánea: qué es, cómo se calcula y ejercicios
La aceleración instantánea es el cambio que experimenta la velocidad por unidad de tiempo en cada instante del movimiento. En el preciso momento en que el “dragster” de la imagen fue fotografiado, llevaba una aceleración de 29,4 m/s2. Esto significa que para ese instante, su velocidad estaba siendo incrementada en 29,4 m/s en el lapso de 1 s. Esto equivale a 105 Km/h en apenas 1 segundo.
Una competencia de dragsters se modela fácilmente suponiendo que el bólido es un objeto puntual P que se mueve en línea recta. Sobre esa línea se elige un eje orientado con origen O que llamaremos el eje (OX) o simplemente eje x.

Las variables cinemáticas que definen y describen el movimiento son:
- La posición x
- El desplazamiento Δx
- La velocidad v
- La aceleración a
Todas ellas son cantidades vectoriales. Por tanto tienen una magnitud, una dirección y un sentido.
En el caso de movimiento rectilíneo solo hay dos direcciones posibles: positiva (+) en el sentido de (OX) o negativo (-) en sentido contrario de (OX). Por lo tanto puede prescindirse de la notación vectorial formal y utilizar los signos para indicar el sentido de la magnitud.
Índice del artículo
- 1 ¿Cómo se calcula la aceleración?
- 2 Velocidad a partir de la aceleración instantánea
- 3 Ejercicios resueltos
- 4 Referencias
Supongamos que en el instante t la partícula tiene velocidad v(t) y en el instante t’ su velocidad es v(t’).
Entonces el cambio que tuvo la velocidad en ese lapso de tiempo fue Δv = v(t’) – v(t). Por lo tanto la aceleración en el lapso de tiempo Δt = t’ – t , estaría dado por el cociente:

Este cociente es la aceleración media am en el lapso de tiempo Δt comprendido entre los instantes t y t’.
Si quisiéramos calcular la aceleración justamente en el instante t, entonces t’ debería ser una cantidad insignificantemente mayor que t. Con ello Δt, que es la diferencia entre ambos, debería ser casi cero.
Matemáticamente se indica así: Δt → 0 y se obtiene:
I) Una partícula se mueve sobre el eje X con velocidad constante v0 = 3 m/s. ¿ Cuál será la aceleración de la partícula?
La derivada de una constante es cero, por lo tanto la aceleración de una partícula que se mueve con velocidad constante es cero.
II) Una partícula se mueve sobre el eje x y su velocidad cambia con el tiempo según la siguiente fórmula:
v(t) = 2 – 3t
Donde la velocidad se mide en m/s y el tiempo en s. ¿Cuál será la aceleración de la partícula?
El resultado se interpreta así: para cualquier instante la aceleración es de -3 m/s.
Entre los instantes 0 s y 2/3 s la velocidad es positiva mientras la aceleración es negativa, es decir en ese intervalo la partícula va disminuyendo su velocidad o desacelerando.
En el instante 2/3 s justamente su velocidad se hace nula, pero como permanece una aceleración de -3 m/s, a partir de ese instante la velocidad se invierte (pasa a ser negativa).
En los instantes posteriores a los ⅔ s la partícula va acelerando, ya que cada vez su velocidad se hace mas negativa, es decir que su rapidez (módulo de la velocidad) va creciendo.
III) En la figura se muestra una curva que representa la velocidad en función del tiempo, para una partícula que se mueve en el eje X. Encuentre el signo de la aceleración en los instantes t1, t2 y t3. Indique también si la partícula va acelerando o desacelerando.
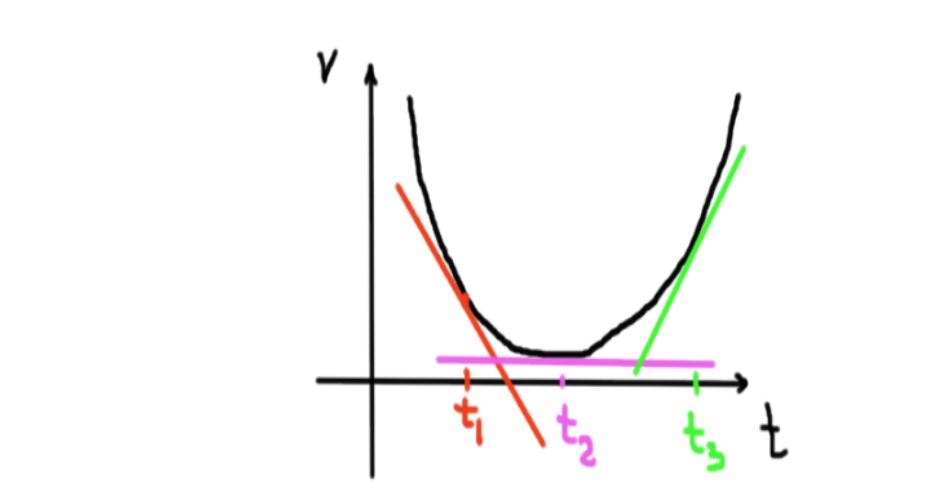
La aceleración es la derivada de la función velocidad, por lo tanto equivale a la pendiente de la recta tangente a la curva v(t) para un instante t dado.
Para el instante t1, la pendiente es negativa, entonces la aceleración es negativa. Y como en ese instante la velocidad es positiva, podemos afirmar que en ese instante la partícula va desacelerando.
Para el instante t2 la recta tangente a la curva v(t) es horizontal, por lo que su pendiente es cero. El móvil tiene aceleración nula, por lo tanto en t2 la partícula ni acelera ni desacelera.
Para el instante t3, la pendiente de la recta tangente a la curva v(t) es positiva. Con una aceleración positiva la partícula realmente va acelerando, porque en ese instante la velocidad también es positiva.
En la sección anterior se definió la aceleración instantánea a partir de la velocidad instantánea. Es decir que si la velocidad es conocida a cada instante, entonces también es posible saber la aceleración en cada instante del movimiento.
El proceso inverso es posible. Es decir conocida la aceleración para cada instante, entonces se podrá calcular la velocidad instantánea.
Si la operación que permite pasar de la velocidad a la aceleración es la derivada, la operación matemática opuesta es la integración.
La aceleración de una partícula que se mueve sobre el eje X es a(t) = ¼ t2. Donde t se mide en segundos y a en m/s. Determine la aceleración y la velocidad de la partícula a los 2 s de movimiento, sabiendo que al instante inicial t0 = 0 estaba en reposo.
Respuesta
A los 2 s la aceleración es de 1 m/s2 y la velocidad para el instante t estará dada por:
Un objeto se mueve a lo largo del eje X con una velocidad en m/s, dada por:
v(t)= 3 t2 – 2 t , donde t se mide en segundos. Determine la aceleración en los instantes: 0s, 1s, 3s.
Respuestas
Tomando la derivada de la v(t) respecto de t se obtiene la aceleración a cualquier instante:
a(t) = 6t -2
Entonces a(0)= -2 m/s2 ; a(1)= 4 m/s2 ; a(3)=16 m/s2 .
Una esfera de metal se suelta desde lo alto de un edificio. La aceleración de caída es la aceleración de gravedad que puede aproximarse por el valor 10 m/s2 y apuntando hacia abajo. Determine la rapidez de la esfera 3 s después de haber sido soltada.
Respuesta
En este problema interviene la aceleración de la gravedad. Tomando como positiva la dirección vertical hacia abajo, se tiene que la aceleración de la esfera es:
a(t) = 10 m/s2
Y la velocidad estará dada por:
Una esfera de metal se dispara hacia arriba con rapidez inicial de 30 m/s. La aceleración del movimiento es la aceleración de gravedad que puede aproximarse por el valor 10 m/s2 y apuntando hacia abajo. Determine la rapidez de la esfera a los 2 s y a los 4 s después de haber sido disparada.
Respuesta
Se tomará como positiva la dirección vertical hacia arriba. En ese caso la aceleración del movimiento estará dada por
a(t) = -10 m/s2
La velocidad como función del tiempo estará dada por:
Al cabo de los 4 s de haber sido disparada la velocidad será 30 – 10∙4 = -10 m/s. Lo que significa que a los 4 s la esfera va en descenso con rapidez de 10 m/s.
- Giancoli, D. Physics. Principles with Applications. 6th Edition. Prentice Hall. 25- 27.
- Resnick, R. (1999). Física. Volumen 1. Tercera edición en español. México. Compañía Editorial Continental S.A. de C.V. 22-27.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Edición. México. Cengage Learning Editores. 25-30.
