Vector director: ecuación de la recta, ejercicios resueltos
Se entiende por vector director aquel que define la dirección de una recta, ya sea en el plano o en el espacio. Por ello, un vector paralelo a la recta, puede ser considerado como un vector director de la misma.
Ello es posible gracias a un axioma de la geometría euclidiana que dice que dos puntos definen una recta. Entonces el segmento orientado que forman esos dos puntos define también un vector director de dicha recta.
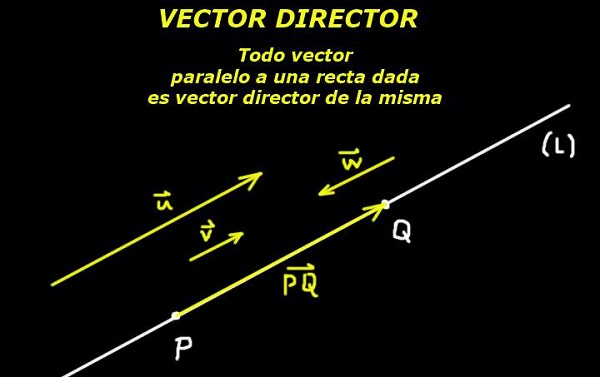
Dado un punto P perteneciente a la recta (L) y dado un vector director u de esa recta, la recta queda completamente determinada.
Índice del artículo
- 1 Ecuación de la recta y vector director
- 2 La recta en forma vectorial
- 3 Forma general de la ecuación de la recta
- 4 Forma estándar de la ecuación de la recta
- 5 Ejercicios resueltos
- 6 Referencias
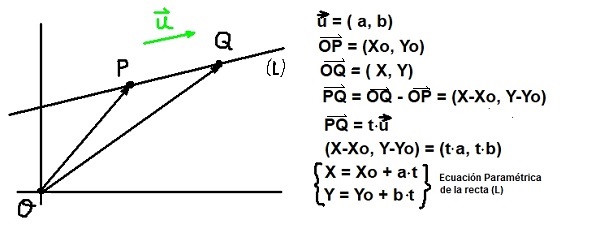
Dado un punto P de coordenadas P:(Xo, Yo) y un vector u director de una recta (L), todo punto Q de coordenadas Q:(X, Y) debe cumplir que el vector PQ sea paralelo a u. Esta última condición se garantiza si PQ es proporcional a u:
PQ = t⋅u
en la expresión anterior t es un parámetro que pertenece a los números reales.
Si se escriben las componentes cartesianas de PQ y de u la ecuación anterior se escribe de la siguiente manera:
(X-Xo, Y-Yo) = t⋅(a, b)
Si se igualan las componentes de la igualdad vectorial se tiene el siguiente par de ecuaciones:
X – Xo = a⋅t y Y – Yo = b⋅t
Las coordenadas X e Y de un punto perteneciente a la recta (L) que pasa por un punto de coordenadas (Xo, Yo) y es paralela al vector directoru=(a, b) se determinan asignando valores reales al parámetro variable t:
{ X = Xo + a⋅t ; Y = Yo + b⋅t }
Ejemplo 1
Para ilustrar el significado de la ecuación paramétrica de la recta, tomamos como vector director
u = (a, b) = (2,-1)
y como punto conocido de la recta el punto
P= (Xo, Yo) = (1, 5).
La ecuación paramétrica de la recta es:
{ X = 1 + 2⋅t ; Y = 5 – 1⋅t ; -∞
Para ilustrar el significado de esta ecuación se muestra la figura 3, en donde el parámetro t va cambiando de valor y el punto Q de coordenadas (X, Y) toma diferentes posiciones sobre la recta.
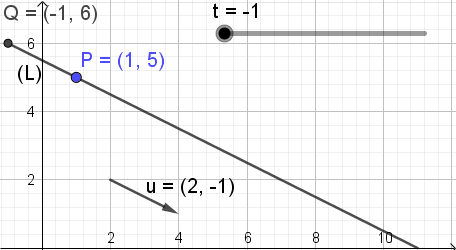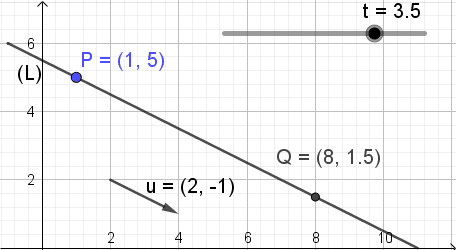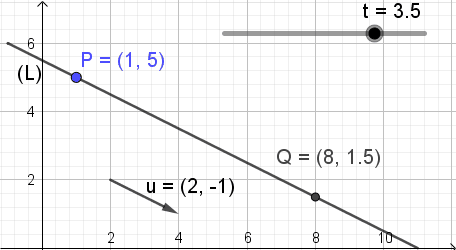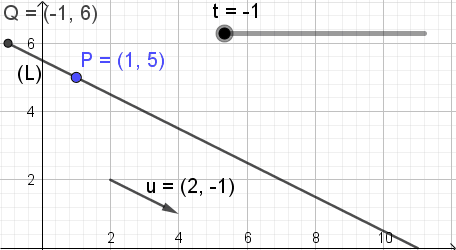
Dado un punto P de la recta y su vector director u puede escribirse la ecuación de la recta en forma vectorial:
OQ = OP + λ⋅u
En la ecuación anterior Q es un punto cualquiera pero perteneciente a la recta y λ un número real.
La ecuación vectorial de la recta es aplicable a cualquier número de dimensiones, incluso puede definirse una hiper-recta.
En el caso tridimensional para un vector director u=(a, b, c) y un punto P=(Xo, Yo, Zo), las coordenadas de un punto genérico Q=(X, Y, Z) perteneciente a la recta es:
(X, Y, Z) = (Xo, Yo, Zo) + λ⋅(a, b, c)
Considere nuevamente la recta que tiene como vector director
u = (a, b) = (2,-1)
y como punto conocido de la recta el punto
P= (Xo, Yo) = (1, 5).
La ecuación vectorial de dicha recta es:
(X, Y) = (1, 5) + λ⋅(2,-1)
Partiendo de la forma paramétrica, despejando e igualando el parámetro λ se tiene:
(X-Xo)/a = (Y-Yo)/b = (Z-Zo)/c
Esta es la forma simétrica de la ecuación de la recta. Note que a, b y c son las componentes del vector director.
Ejemplo 3
Considere la recta que tiene como vector director
u = (a, b) = (2,-1)
y como punto conocido de la recta el punto
P= (Xo, Yo) = (1, 5). Halle su forma simétrica.
La forma simétrica o continua es de la recta es:
(X – 1)/2 = (Y – 5)/(-1)
Se conoce como la forma general de la recta en el plano XY a la ecuación que tiene la siguiente estructura:
A⋅X + B⋅Y = C
La expresión de la forma simétrica puede ser reescrita de modo que tenga la forma general:
b⋅X – a⋅Y = b⋅Xo – a⋅Yo
comparando con la forma general de la recta queda:
A= b, B= -a y C= b⋅Xo – a⋅Yo
Encontrar la forma general de la recta cuyo vector director es u=(2, -1)
y que pasa por el punto P=(1, 5).
Para encontrar la forma general podemos usar las fórmulas dadas, sin embargo se optará por un camino alternativo.
Comenzamos por encontrar el vector dual w del vector director u, definido como el vector que se obtiene intercambiando las componentes de u y multiplicando por -1 la segunda:
w= (-1, -2)
el vector dual w corresponde a una rotación en 90° en sentido horario del vector director v.
Multiplicamos escalarmente w con (X,Y) y con (Xo,Yo) e igualamos:
(-1, -2)•(X, Y) = (-1, -2)•(1, 5)
-X-2Y = -1 -2⋅5= -11
quedando finalmente:
X + 2Y = 11
Se conoce como forma estándar de la recta en el plano XY, aquella que tiene la siguiente estructura:
Y = m⋅X + d
donde m representa la pendiente y d la intercepción con el eje Y.
Dado el vector director u=(a, b) , la pendiente m es b/a.
Y d se obtiene sustituyendo X e Y por el punto conocido Xo, Yo :
Yo = (b/a)Xo + d.
En definitiva m=b/a y d=Yo -(b/a)Xo
Note que la pendiente m es el cociente entre la componente y del vector director y la componente x del mismo.
Encontrar la forma estándar de la recta cuyo vector director es u=(2, -1)
y que pasa por el punto P=(1, 5).
m = -½ y d = 5 – (-½)1 = 11/2
Y = (-1/2)X + 11/2
Encuentre un vector director de la recta (L) que es la intersección del plano (Π): X – Y + Z = 3 y el plano (Ω): 2X + Y = 1.
Luego escriba la forma continua de la ecuación de la recta (L).
Solución
De la ecuación del plano (Ω) despejo Y: Y = 1 -2X
Luego sustituimos en la ecuación del plano (Π):
X – (1 – 2X) + Z = 3 ⇒ 3X + Z = 4 ⇒ Z = 4 – 3X
Luego parametrizamos X, elegimos la parametrización X = λ
Esto significa que la recta tiene ecuación vectorial dada por:
(X, Y, Z) = (λ, 1 – 2λ, 4 – 3λ)
que puede ser reescrita como:
(X, Y, Z) =(0, 1, 4) + λ(1, -2, -3)
con lo que queda claro que el vector u = (1, -2, -3) es un vector director de la recta (L).
La forma continua de la recta (L) es:
(X – 0)/1 = (Y – 1)/(-2) = (Z – 4)/(-3)
Dado el plano 5X + a Y + 4Z = 5
y la recta cuya ecuación es X/1 = (Y-2)/3 = (Z -2)/(-2)
Determine el valor de a de modo tal que el plano y la recta sean paralelos.
Solución 2
El vector n = (5, a, 4) es un vector normal al plano.
El vector u = (1, 3, -2) es un vector director de la recta.
Si la recta es paralela al plano, entonces n•v = 0.
(5, a, 4)•(1, 3, -2)= 5 +3a -8 = 0 ⇒ a=1.
- Fleming, W., & Varberg, D. E. (1989). Precalculus Mathematics. Prentice Hall PTR.
- Kolman, B. (2006). Álgebra lineal. Pearson Educación.
- Leal, J. M., & Viloria, N. G. (2005). Geometría Analítica Plana. Mérida – Venezuela: Editorial Venezolana C. A.
- Navarro, Rocio. Los vectores. Recobrado de: books.google.co.ve.
- Pérez, C. D. (2006). Precalculo. Pearson Educación.
- Prenowitz, W. 2012. Basic Concepts of Geometry. Rowman & Littlefield.
- Sullivan, M. (1997). Precalculo. Pearson Educación.
