Elementos de un vector y sus características
Los elementos de un vector son la dirección, la distancia y el modulo. En la matemática, la física y la ingeniería, un vector es un objeto geométrico que tiene una magnitud (o longitud) y dirección. De acuerdo a la álgebra de vectores, los vectores pueden ser sumados a otros vectores.
Un vector es lo que se necesita para llevar el punto A al punto B. Los vectores juegan un rol importante en la física: la velocidad y la aceleración de un objeto en movimiento y las fuerzas que actúan en él pueden ser descritas con vectores.
Muchas otras cualidades físicas pueden ser pensadas como vectores. La representación matemática de un vector físico depende del sistema de coordenadas usado para describirlo.
Existen varias clases de vectores, entre ellos podemos encontrar los vectores deslizantes, los vectores colineales, los vectores concurrentes, los vectores de posición, los vectores libres, los vectores paralelos y los vectores coplanares, entre otros.
Elementos de un vector
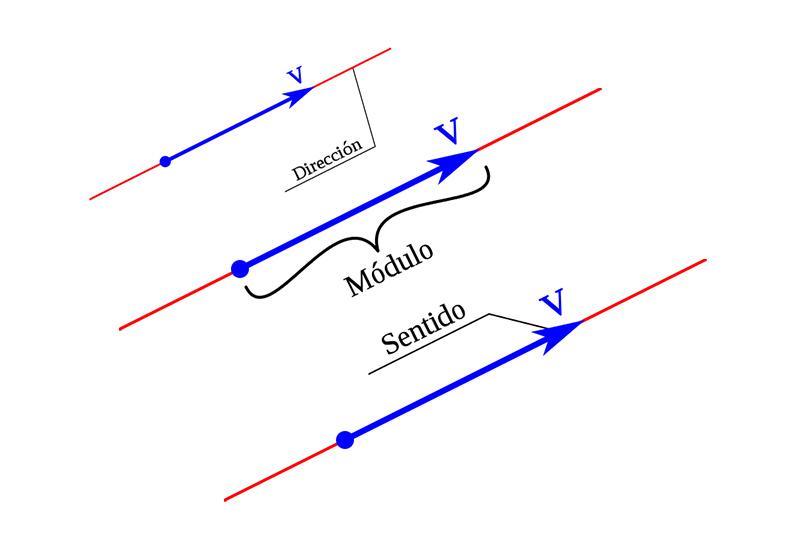
Principalmente un vector tiene tres elementos: la dirección, el sentido, y el módulo.
Un vector es una entidad que tiene magnitud y dirección. Ejemplos de vectores incluyen desplazamiento, velocidad, aceleración, y fuerza. Para describir una de estas cantidades vectoriales, es necesario encontrar la magnitud y la dirección.
Por ejemplo, si la velocidad de un objeto es de 25 metros por segundo, entonces la descripción de la velocidad del objeto está incompleta, ya el objeto puede estar moviéndose a 25 metros por segundo al sur, o a 25 metros por segundo al norte, o a 25 metros por segundo al sudeste.
Para poder describir por completo la velocidad de un objeto, se deben definir ambas: tanto la magnitud de 25 metros por segundo, como la dirección, como por ejemplo al sur.
Para que tales descripciones de las cantidades vectoriales sean útiles, es importante que todo el mundo llegue a un acuerdo en cómo la dirección del objeto es descrita.
La mayoría de las personas están acostumbradas a la idea de que en un mapa se refiere la dirección este si se mira a la derecha. Pero esto es una mera convención que los realizadores de mapas han usado por años para que todo el mundo pueda estar de acuerdo.
Entonces, ¿cuál es la dirección de una cantidad vectorial que no se dirige hacia el norte o hacia el este sino en algún lugar entre el norte y el este? Para estos casos es importante que exista alguna convención para describir la dirección de dicho vector.
Esta convención es referida como la CCW. Usando esta convención podemos describir la dirección de cualquier vector en términos de su ángulo de rotación hacia la izquierda.
Utilizando esta convención, la dirección norte sería a 90°, ya que si un vector está apuntando hacia el este tendría que ser rotado 90° hacia la dirección izquierda para alcanzar el punto norte.
Asimismo, la dirección al oeste sería ubicada a 180°, ya que un vector que apunta al oeste tendría que ser rotado 180° hacia la izquierda para apuntar al punto oeste.
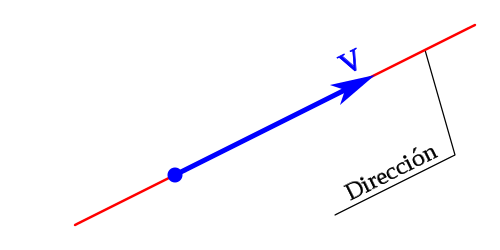
Dicho de otra manera, la dirección de un vector se representará a través de una recta contenida en el vector o de cualquier recta que se encuentre paralela a la misma,
Se determinará por el ángulo que se forma entre el vector y cualquier otra recta de referencia. O sea que la dirección de la recta que está en el vector o alguna recta paralela a ella es la dirección del vector.
Sentido
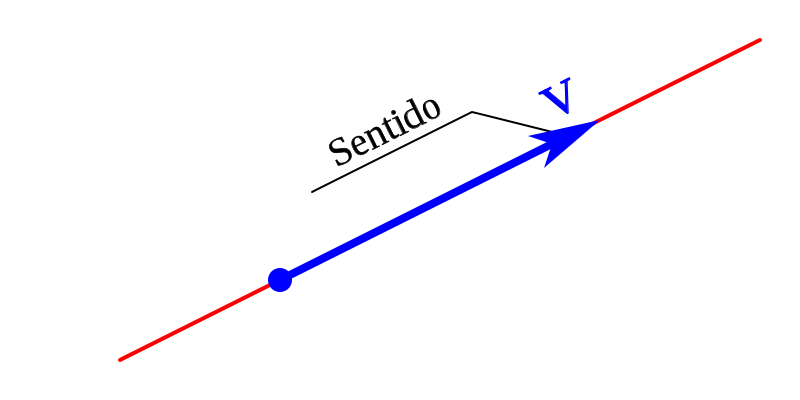
El sentido del vector se refiere al elemento que describe como va el punto A hacia el extremo B:
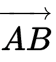
El sentido de un vector está especificado por el orden de dos puntos en una línea paralela al vector, a diferencia de la dirección del vector que es especificada por la relación entre el vector y cualquier línea de referencia y/o plano.
Tanto la orientación como el sentido determinan la dirección de un vector. La orientación dice a que ángulo se encuentra el vector, y el sentido dice hacia dónde está apuntando.
La dirección del vector solamente establece el ángulo que realiza un vector con su axis horizontal, pero eso puede crear ambigüedad ya que la flecha puede apuntar en dos direcciones opuestas e igual realizar el mismo ángulo.
El sentido aclara esta ambigüedad e indica hacia dónde está apuntando la flecha o hacia donde se dirige el vector.
De alguna manera el sentido nos dice el orden en el cual leer el vector. Indica donde comienza y donde termina el vector.
Módulo
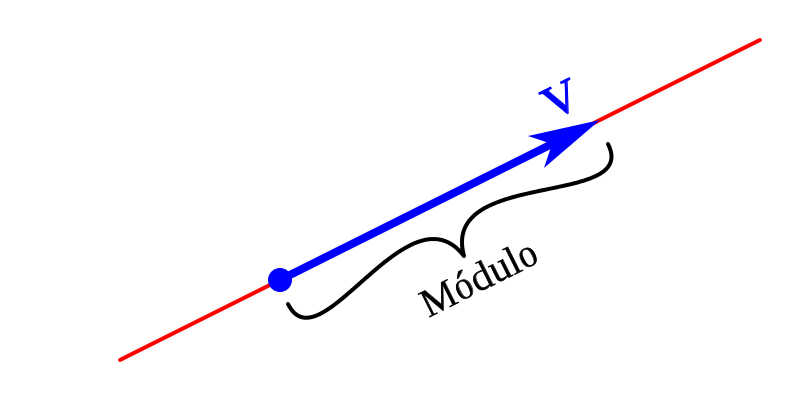
El módulo o amplitud de un vector puede ser definido como la longitud del segmento AB. El módulo se puede representar a través de una longitud que sea proporcional al valor que tiene el vector. El módulo de un vector siempre será cero, o en otros casos algún número positivo.
En matemáticas, el vector será definido por su distancia euclidiana (módulo), dirección y sentido.
La distancia euclidiana o distancia euclídea, es la distancia ‘ordinaria’ en línea recta entre dos puntos ubicados en un espacio euclidiano. Con esta distancia, el espacio euclidiano se convierte en espacio métrico.
Una distancia euclidiana entre dos puntos, por ejemplo P y Q, es la distancia entre el segmento de línea que los conecta:
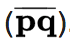
La posición de un punto en un espacio euclidiano n es un vector. Así, P y Q son vectores, comenzando desde el origen del espacio y sus puntas indicando dos puntos.
La norma euclidiana, magnitud, o distancia euclidiana de un vector mide la longitud de dicho vector.
Referencias
- Vector direction. Recuperado de physicsclassroom.com.
- What is the sense of a vector? Recuperado de physics.stackexchange.com.
- What’s the difference between direction, sense, and orientation? Recuperado de math.stackexchange.com.
- Euclidean distance. Recuperado de wikipedia.org.
