¿Qué es la notación decimal? (Con ejemplos)

¿Qué es la notación decimal?

La notación decimal consiste en escribir un número real mediante una parte entera y una parte decimal, ambas separadas por un punto o una coma. La parte entera está a la izquierda y la parte decimal a la derecha de dicho punto.

El 0 puede aparecer tanto en la parte entera como en la decimal. Por ejemplo, las siguientes cifras son números decimales:

• 0.25
• 1.5903
• 4,19367

Nótese que la parte decimal de estos números es finita, pero también hay números con una parte decimal infinita, como 0,33333…, donde se colocan puntos suspensivos como una forma de indicar que el número de decimales prosigue indefinidamente.

En forma general, un número decimal finito se puede escribir como:

N.a₁a₂a₃…a_n

Siendo N un número entero y n la cantidad de decimales, mientras que un decimal infinito adopta la forma:

N.a₁a₂a₃…

En el decimal 0.25 se identifican:

• N = 0
• a₁ = 2
• a₂ = 5

Los decimales surgen como otra forma de expresar los números racionales, que son aquellos con forma de fracción o quebrado. De hecho, cualquier fracción se puede escribir en notación decimal, como se verá enseguida.

También sirven para representar números que no se derivan de una fracción, los llamados números irracionales, como son: π, √2, √3, √5, el número “e” y muchos otros más.

Ejemplos de números decimales

Un número decimal se puede obtener a partir de una fracción de una forma muy simple: calculando el cociente del numerador entre el denominador. Si el denominador es la unidad seguida de ceros, esto es muy sencillo:

• 8/10 = 0.8
• −(5/100) = −0.05

En el primer caso, como el denominador es 10, se coloca el punto decimal inmediatamente a la izquierda del 8 y el decimal 0.8 se lee “8 décimas” o “cero punto ocho”.

En el segundo caso, dado que el denominador es 100, hay que poner el punto decimal dos lugares a la izquierda del 5, y dado que el número es negativo, se lee “menos 5 centésimas” o “menos cero punto cero cinco”.

Cuando el denominador no es la unidad seguida de 0, se emplea la división larga:

Obsérvese que para llevar a cabo esta división, como el numerador es menor que el denominador, se multiplicó primero por 10 y al hacerlo, se coloca un 0 seguido del punto decimal en el cociente, para no alterar la operación. Luego se procede normalmente a dividir 10 entre 2 que es igual a 5 y el residuo de la división es 0.

La forma decimal de la fracción ½ es 0.5, que se lee “cero punto cinco”:

La fracción 7/8 es otro ejemplo. Como 7 es menor que 8, se multiplica 7×10 = 70, se coloca un 0 en el cociente seguido del punto decimal y se divide normalmente:

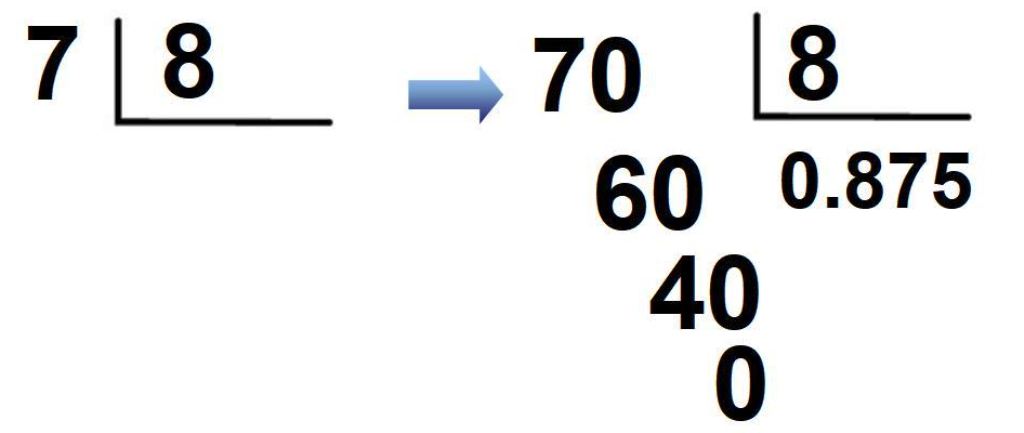
El resultado es que la fracción se escribe en notación decimal como:

7/8 = 0.875

Este número, al igual que el resultado anterior, es un decimal finito y una manera de leerlo es: “cero punto ochocientos setenta y cinco”. Mediante este procedimiento también se escriben en notación decimal las siguientes fracciones:

8/10 = 0.8

5/7 = 0.714285714…

9/20 = 0.45

3/8 = 0.375

Nótese que como en todos estas fracciones el numerador es menor que el denominador, la parte entera de los decimales resultantes es 0. Sin embargo, un número mixto o una fracción impropia (aquella cuyo numerador es mayor que su denominador) también tiene representación decimal.

En tal caso la parte entera es mayor o igual que 1 si la fracción es positiva, y menor que –1 si es negativa:

9/4 = 2.25

10/3 = 3.333333…

−12/5 = −2.4

1 ½ = 1.5

2 ¾ = 2.75

Parte entera y parte fraccionaria de los decimales negativos

En los ejemplos anteriores se observó que para encontrar la expresión decimal de una fracción simplemente se divide numerador y denominador. Aun si la fracción es negativa, simplemente el signo menos se antepone a la expresión decimal equivalente.

No obstante, la parte entera y la parte fraccionaria de un decimal difieren según el signo que lleve.

Cuando un decimal es positivo, como 2.25, su parte entera es 2 y su parte decimal es 0.25 y el número se puede escribir como la suma de la parte entera y la parte decimal, así:

2.25 = 2 + 0.25

La parte entera se define como el entero inmediatamente menor al decimal y la parte decimal es positiva siempre. Para 2.25, el entero inmediatamente menor es 2.

Pero en el caso de la fracción −12/5, equivalente al decimal −2.4 lo anterior no funciona.

−2 + 0.4 = −1.6 ≠ −2.4

Por lo tanto, la parte entera de −2.4 no puede ser −2 sino el entero inmediatamente menor: −3. Pero en ese caso, la parte fraccionaria no sería 0.4, ya que al sumar:

−3 + 0.4 = −2.6 ≠ −2.4

¿Entonces, cuál es la parte decimal del número negativo −2.4? Se halla restando el número decimal de su parte entera y el resultado siempre va a ser positivo:

−2.4 −(−3) = 0.6

Por último se comprueba que al sumar la parte entera y la parte fraccionaria se obtiene el decimal buscado:

−3 + 0.6 = −2.4

El procedimiento para hallar parte entera y parte decimal de cualquier número, sin importar el signo, se resume de esta forma:

• La parte entera es el entero inmediatamente menor al número decimal.
• La parte decimal se calcula restando el decimal de su parte entera.

Sin embargo, para propósitos prácticos de cálculo, el número decimal −2.4 se puede descomponer como − (2 + 0.4) = − 24/10  o bien:

Tipos de decimales

Hay números decimales cuya parte decimal es finita o bien infinita, lo cual se usa como criterio de clasificación:

Decimales finitos o exactos

Cuando los decimales son finitos, como por ejemplo 0.125, también se dice que son decimales exactos.

Decimales infinitos

Se obtiene un decimal infinito cuando el residuo de la división entre numerador y denominador nunca se hace 0.

Siempre que el decimal provenga del cociente entre dos enteros, esta parte decimal es periódica, es decir, está compuesta de un o varias cifras que se repiten indefinidamente, llamada período.

Por ejemplo, el número 3.333333… originado por la fracción impropia 10/3, es un decimal periódico: la parte entera es 3, y luego del punto decimal, el número 3 se repite indefinidamente. Esto se puede simbolizar colocando una curva o sombrero encima del número que se repite:

Por último están los decimales infinitos que no son periódicos, los cuales no se originan del cociente entre dos números enteros. Como se mencionó al principio, estos decimales pertenecen al conjunto de los números irracionales, como el número pi, por ejemplo.

Ejercicios resueltos

Ejercicio 1

Escribir en forma numérica los siguientes números decimales:

a) Cero punto cuatrocientos cuarenta y siete
b) Cinco milésimas
c) Dos unidades y cinco centésimas
d) Tres punto veintisiete negativo
e) Uno punto ochocientos veinte y cuatro mil quinientos sesenta y tres

• Solución

a) 0.447

b) 0.005

c) 2.05

d) −3.27

e) 1.824563

Ejercicio 2

Clasificar los siguientes números decimales en decimales exactos, periódicos puros, periódicos mixtos o números irracionales. En todos los casos indicar el valor de la parte entera, y en caso de ser periódicos o periódicos mixtos, señalar asimismo el valor del período y el ante-período, según corresponda:

a) 0.35627

b) 1,21212121…

c) −1.32

d) 1.414213562…= √2

• Solución

a) 35627 es un decimal exacto. Su parte entera es 0 y su parte decimal es 0.35627.

b) 1,21212121… es un decimal infinito y periódico puro, la parte entera es 1 y el período es 21.

c) −1.32 es un decimal exacto y negativo, cuya parte entera es −2. La parte decimal se calcula restando el número decimal de la parte entera:

−1.32 − (−2) = 0.68

d) La expresión decimal de √2 es infinita y no periódica, puesto que es un número irracional.

Es un decimal periódico mixto, la parte entera es 3, el ante-período es 1 y el período es 89.

Referencias

1. Aportes pedagógicos y material didáctico. Notación decimal. Recuperado de: tecdigital.tec.ac.cr.
2. Baldor, A. 2007. Aritmética teórico práctica. Grupo Editorial Patria S.A. de C.V.
3. Math for Trades. Understanding Decimal Notation. Recuperado de: opentextbc.ca.
4. UNAM. Números racionales: significados y representaciones. Recuperado de: redi.codeic.unam.mx.