Desigualdad del triángulo: demostración, ejemplos, ejercicios resueltos
Se denomina desigualdad del triángulo a la propiedad que cumplen dos números reales consistentes en que el valor absoluto de su suma siempre es menor o igual a la suma de sus valores absolutos. Esta propiedad también es conocida como desigualdad de Minkowski o desigualdad triangular.
Esta propiedad de los números se denomina desigualdad triangular porque en los triángulos ocurre que la longitud de un lado siempre es menor o igual que la suma de los otros dos, aun cuando esta desigualdad no siempre se aplique en el ámbito de los triángulos.

Existen varias demostraciones de la de la desigualdad triangular en los números reales, pero en este caso elegiremos una basada en las propiedades del valor absoluto y del binomio al cuadrado.
Teorema: Para todo par de números a y b perteneciente a los números reales se tiene que:
| a + b | ≤ | a | + | b |
Índice del artículo
Comenzamos por considerar el primer miembro de la desigualdad, el cual se elevará al cuadrado:
| a + b |^2 = ( a + b )^2 = a^2 + 2 a b + b^2 (ec. 1)
En el paso anterior se ha usado la propiedad que un número cualquiera elevado al cuadrado es igual al valor absoluto de dicho número elevado al cuadrado, es decir: |x|^2 = x^2. También se ha usado el desarrollo del binomio al cuadrado.
Todo número x es menor o igual que su valor absoluto. Si el número es positivo vale la igualdad, pero si el número es negativo el mismo será siempre menor que un número positivo. En este caso su propio valor absoluto, es decir que puede afirmarse que x ≤ | x |.
El producto (a b) es un número, por tanto se aplica que (a b) ≤ | a b |. Cuando se aplica esta propiedad a la (ec. 1) nos queda:
| a + b |^2 = a^2 + 2 (a b) + b^2 ≤ a^2 + 2 | a b | + b^2 (ec. 2)
Teniendo en cuenta que | a b |=| a || b | la (ec. 2) puede ser escrita de la siguiente manera:
| a + b |^2 ≤ a^2 + 2 | a || b | + b^2 (ec. 3)
Pero como hemos dicho antes que el cuadrado de un número es igual al valor absoluto del número elevado al cuadrado, entonces la ecuación 3 puede ser reescrita de la siguiente forma:
| a + b |^2 ≤ |a|^2 + 2 |a| |b| + |b|^2 (ec. 4)
En el segundo miembro de la desigualdad se reconoce un producto notable, el cual al ser aplicado conduce a:
| a + b |^2 ≤ (|a|+ |b|)^2 (ec. 5)
En la expresión anterior debe notarse que los valores a elevar al cuadrado en ambos miembros de la desigualdad son positivos por tanto ha de cumplirse también que:
| a + b | ≤ (|a|+ |b|) (ec. 6)
La expresión anterior es exactamente lo que se quería demostrar.
A continuación comprobaremos la desigualdad triangular con varios ejemplos.
Se toma el valor a =2 y el valor b = 5, es decir ambos números positivos y comprobamos si se cumple o no la desigualdad.
| 2 + 5 | ≤ |2|+ |5|
| 7 | ≤ |2|+ |5|
7 ≤ 2+ 5
Se verifica la igualdad, por tanto se ha cumplido el teorema de la desigualdad del triángulo.
Se eligen los siguientes valores a =2 y b = -5, es decir un número positivo y el otro negativo, comprobamos si se cumple o no la desigualdad.
| 2 – 5 | ≤ |2|+ |-5|
| -3 | ≤ |2|+ |-5|
3 ≤ 2 + 5
Se cumple la desigualdad, por tanto se ha verificado el teorema de la desigualdad triangular.
Se toma el valor a = -2 y el valor b = 5, es decir un número negativo y el otro positivo, comprobamos si se cumple o no la desigualdad.
| -2 + 5 | ≤ |-2|+ |5|
| 3 | ≤ |-2|+ |5|
3 ≤ 2 + 5
Se verifica la desigualdad, por tanto se ha cumplido el teorema.
Se eligen los siguientes valores a =-2 y b = -5, es decir ambos números negativos y comprobamos si se cumple o no la desigualdad.
| -2 – 5 | ≤ |-2|+ |-5|
| -7 | ≤ |-2|+ |-5|
7 ≤ 2+ 5
Se verifica la igualdad, por tanto se ha cumplido el teorema de la desigualdad de Minkowski.
Se toma el valor a =0 y el valor b = 5, es decir un número cero y el otro positivo, a continuación comprobamos si se cumple o no la desigualdad.
| 0 + 5 | ≤ |0|+ |5|
| 5 | ≤ |0|+ |5|
5 ≤ 0+ 5
Se cumple la igualdad, por tanto se ha verificado el teorema de la desigualdad del triángulo.
Se toma el valor a =0 y el valor b = -7, es decir un número cero y el otro positivo, a continuación comprobamos si se cumple o no la desigualdad.
| 0 – 7 | ≤ |0|+ |-7|
| -7 | ≤ |0|+ |-7|
7 ≤ 0+ 7
Se verifica la igualdad, por tanto se ha cumplido el teorema de la desigualdad triangular.
En los siguientes ejercicios represente geométricamente la desigualdad del triángulo o desigualdad de Minkowski para los números a y b.
El número a se representará como un segmento en el eje X, su origen O coincide con el cero del eje X y el otro extremo del segmento (en el punto P) estará en la dirección positiva (hacia la derecha) del eje X si a > 0, pero si a 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.
De forma similar el número b se representará como un segmento cuyo origen está sobre el punto P. El otro extremo, es decir el punto Q estará a la derecha de P si b es positivo (b>0) y el punto Q estará |b| unidades a la izquierda de P si b0.
Represente gráficamente la desigualdad del triángulo para a= 5 y b= 3 | a + b | ≤ | a | + | b |, siendo c = a + b.
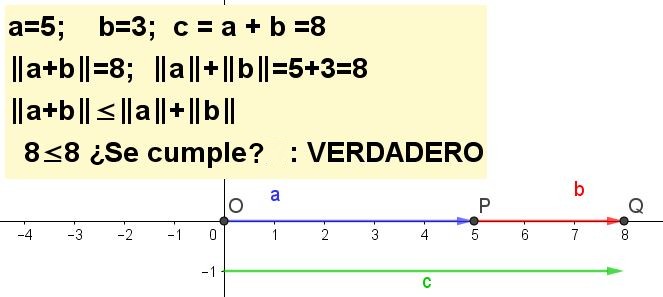
Realizar un gráfico de la desigualdad triangular para a= 5 y b= -3.
| a + b | ≤ | a | + | b |, siendo c = a + b.

Mostrar gráficamente la desigualdad del triángulo para a = -5 y b = 3.
| a + b | ≤ | a | + | b |, siendo c = a + b.
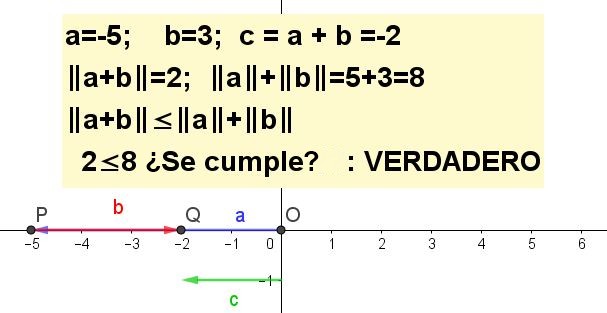
Construir gráficamente la desigualdad triangular para a = -5 y b = -3.
| a + b | ≤ | a | + | b |, siendo c = a + b.
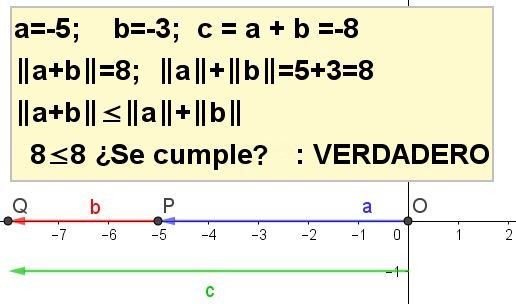
- E. Whitesitt. (1980).Álgebra Booleana y sus Aplicaciones . Compañía Editorial Continental C. A.
- Mícheál O’ Searcoid.(2003) Elements of Abstract Analysis. . Department of mathematics. University college Dublin, Beldfield, Dublind.
- J. Van Wyk. (2006) Mathematics and Engineering in Computer Science. Institute for Computer Sciences and Technology. National Bureau of Standards. Washington, D. C. 20234
- Eric Lehman. Mathematics for Computer Science. Google Inc.
- F Thomson Leighton (1980). Calculus. Department of Mathematics and the Computer Science and AI Laboratory, Massachussetts Institute of Technology.
- Khan Academy. Triangle Inequality Theorem. Recuperado de: khanacademy.org
- Wikipedia. Desigualdad triangular. Recuperado de: es. wikipedia.com
