Período de la función y=3sen(4x)
El período de la función y=3sen(4x) es 2π/4=π/2. Para comprender con claridad el porqué de esta afirmación se debe conocer la definición de período de una función y el período de la función sen(x); un poco sobre gráfica de funciones también será de utilidad.
Las funciones trigonométricas, como el seno y el coseno (sen(x) y cos(x)), son de gran utilidad tanto en las matemáticas como en la ingeniería.
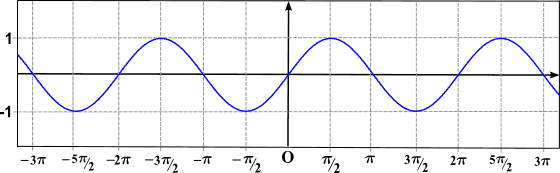
La palabra período hace mención a la repetición de un evento, de modo que decir que una función es periódica es equivalente a decir “su gráfica es la repetición de un trozo de curva”. Como se aprecia en la imagen anterior, la función sen(x) es periódica.
Funciones periódicas
Una función f(x) se dice que es periódica si existe un valor real p≠0 tal que f(x+p)=f(x) para todo x en el dominio de la función. En este caso, el período de la función es p.
Generalmente se llama período de la función al menor número real positivo p que satisfaga la definición.
Como se aprecia en la gráfica anterior, la función sen(x) es periódica y su período es 2π (la función coseno también es periódica, con período igual a 2π).
Alteraciones en la gráfica de una función
Sea f(x) una función cuya gráfica es conocida, y sea c una constante positiva. ¿Qué le sucede a la gráfica de f(x) si se multiplica f(x) por c? En otras palabras, ¿cómo es la gráfica de c*f(x) y f(cx)?
Gráfica de c*f(x)
Al multiplicar una función, de manera externa, por una constante positiva, la gráfica de f(x) sufre un cambio en los valores de salida; es decir, el cambio es de forma vertical y se pueden tener dos casos:
– Si c>1, entonces la gráfica sufre un estiramiento vertical con un factor de c.
– Si 0 Cuando se multiplica el argumento de una función por una constante, la gráfica de f(x) sufre un cambio en los valores de entrada; es decir, el cambio es de forma horizontal y, al igual que antes, se pueden tener dos casos: – Si c>1, entonces la gráfica sufre una compresión horizontal con un factor de 1/c. – Si 0 Cabe destacar que en la función f(x)=3sen(4x) hay dos constantes que alteran a la gráfica de la función seno: una multiplicando de manera externa y otra de manera interna. El 3 que está fuera de la función seno lo que hace es alargar la función verticalmente por un factor de 3. Esto implica que la gráfica función 3sen(x) estará entre los valores -3 y 3. El 4 que está dentro de la función seno hace que la gráfica de la función sufra una compresión horizontal por un factor de 1/4. Por otro lado, el período de una función se mide de forma horizontal. Como el período de la función sen(x) es 2π, al considerar sen(4x) el tamaño del período cambiará. Para saber cuál es el período de y=3sen(4x) basta con multiplicar el período de la función sen(x) por 1/4 (el factor de compresión). En otras palabras, el período de la función y=3sen(4x) es 2π/4=π/2, como se puede apreciar en la última gráfica.Gráfica de f(cx)
Período de la función y=3sen(4x)
