Tipos de triángulos y sus características (con ejemplos)
Un triángulo es un polígono o figura geométrica que tiene tres lados, tres vértices y tres ángulos. Los lados son cada una de las líneas rectas que lo forman. Los vértices son los puntos donde se unen los lados; los ángulos son los arcos o aberturas que se forman cerca de los vértices, al unirse dos lados.
Un triángulo también puede ser definido como el área determinada por tres rectas. La suma de sus tres ángulos siempre es igual a 180º. La longitud de cualquiera de sus lados es siempre menor que el resultado de la suma de la longitud de los otros dos lados, pero mayor que su resta.
Los triángulos son las figuras geométricas más sencillas, y sirven para investigar las propiedades matemáticas de otras figuras más complejas, como pentágonos o hexágonos.
También se emplean en otras ciencias, como la topografía, la navegación o la astronomía. En esta última se emplean para conocer la distancia que nos separa de un cuerpo celeste lejano a partir de dos puntos de observación situados en la Tierra. Este método es conocido como paralaje.
Los triángulos se clasifican de acuerdo con la longitud de sus lados o según la amplitud de sus ángulos.
Tipos de triángulos según sus lados
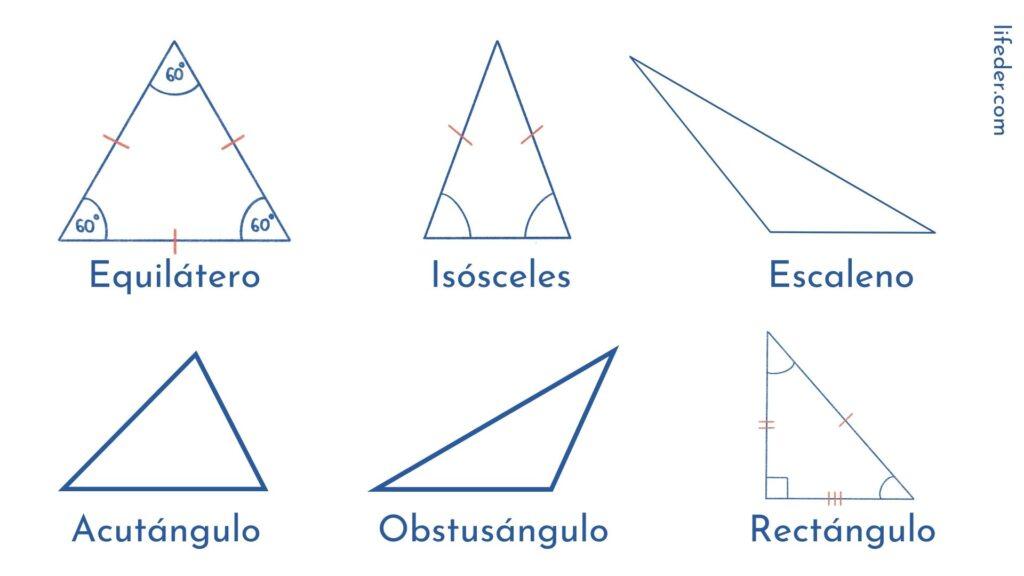
Triángulo equilátero

Los lados de este tipo de triángulo tienen exactamente la misma longitud. Y lo mismo ocurre con sus ángulos: los tres miden 60º. Por eso decimos que el triángulo equilátero es un polígono regular.
Triángulo escaleno

Al contrario del equilátero, en el triángulo escaleno todo es desigual: sus tres lados poseen longitudes distintas y sus ángulos difieren en amplitud.
Triángulo isósceles

En este tipo de triángulo hallamos que dos lados poseen la misma medida, mientras que el lado restante es diferente. Lo mismo se observa en la amplitud de los ángulos: dos son iguales y uno diferente.
Tipos de triángulos según sus ángulos
Triángulo rectángulo

Se caracteriza por poseer un ángulo recto, es decir, de 90º. Sus otros dos ángulos son agudos o menores de 90º.
En este tipo de triángulos el lado más largo recibe el nombre de hipotenusa, mientras que otros dos lados son los catetos.
Triángulo oblicuángulo
Pertenecen a este tipo los triángulos que no poseen ningún ángulo recto. Se subdividen en dos tipos:
Triángulo acutángulo: sus tres ángulos son agudos.

Triángulo obtusángulo: poseen dos ángulos agudos y uno obtuso o mayor de 90º.

Triángulos mixtos
Un mismo triángulo puede ser clasificado de acuerdo con los dos criterios, es decir, de acuerdo con la longitud de sus lados y la amplitud de sus ángulos.
Por ejemplo, un triángulo rectángulo puede ser también escaleno o isósceles, pero no podría ser equilátero, ya que este último no presenta ningún ángulo recto.
Sin embargo, un triángulo equilátero podría ser acutángulos, pues efectivamente tiene tres ángulos agudos o menores de 90º.

Un triángulo escaleno puede ser al mismo tiempo obtusángulo, pues tanto la amplitud de sus ángulos como la longitud de sus lados son diferentes.
¿Cómo calcular el perímetro de un triángulo?
Se llama perímetro al producto de la suma de la longitud de los tres lados de un triángulo.
Veamos algunos ejemplos.
1- Se nos pide que hallemos el perímetro de un triángulo escaleno cuyos lados 6, 8 y 4 centímetros. Todo lo que tenemos que hacer es sumar:
6 + 8 + 4 = 18
Por tanto, el perímetro de este triángulo escaleno es de 10 centímetros.
2- A continuación nos piden que calculemos el perímetro de un triángulo isósceles cuyos lados miden 4 centímetros los dos iguales y 6 centímetros el lado restante. Puesto que dos de sus lados tienen igual longitud, debemos colocar dos veces la misma cifra, así:
4 + 4 + 6 = 14
El perímetro de este triángulo es de 14 centímetros.
3- Un último ejemplo. Tenemos la tarea de determinar el perímetro de un triángulo equilátero de 9 centímetros de lado. Como ya conocemos las características de los diversos tipos de triángulos, sabemos que el equilátero se distingue porque sus tres lados son iguales. Por lo tanto:
9 + 9 + 9 = 27
El perímetro de este equilátero es de 27 centímetros.
Mediatrices, bisectrices y medianas
Se trata de los tres tipos de líneas rectas que se pueden trazar en un triángulo.
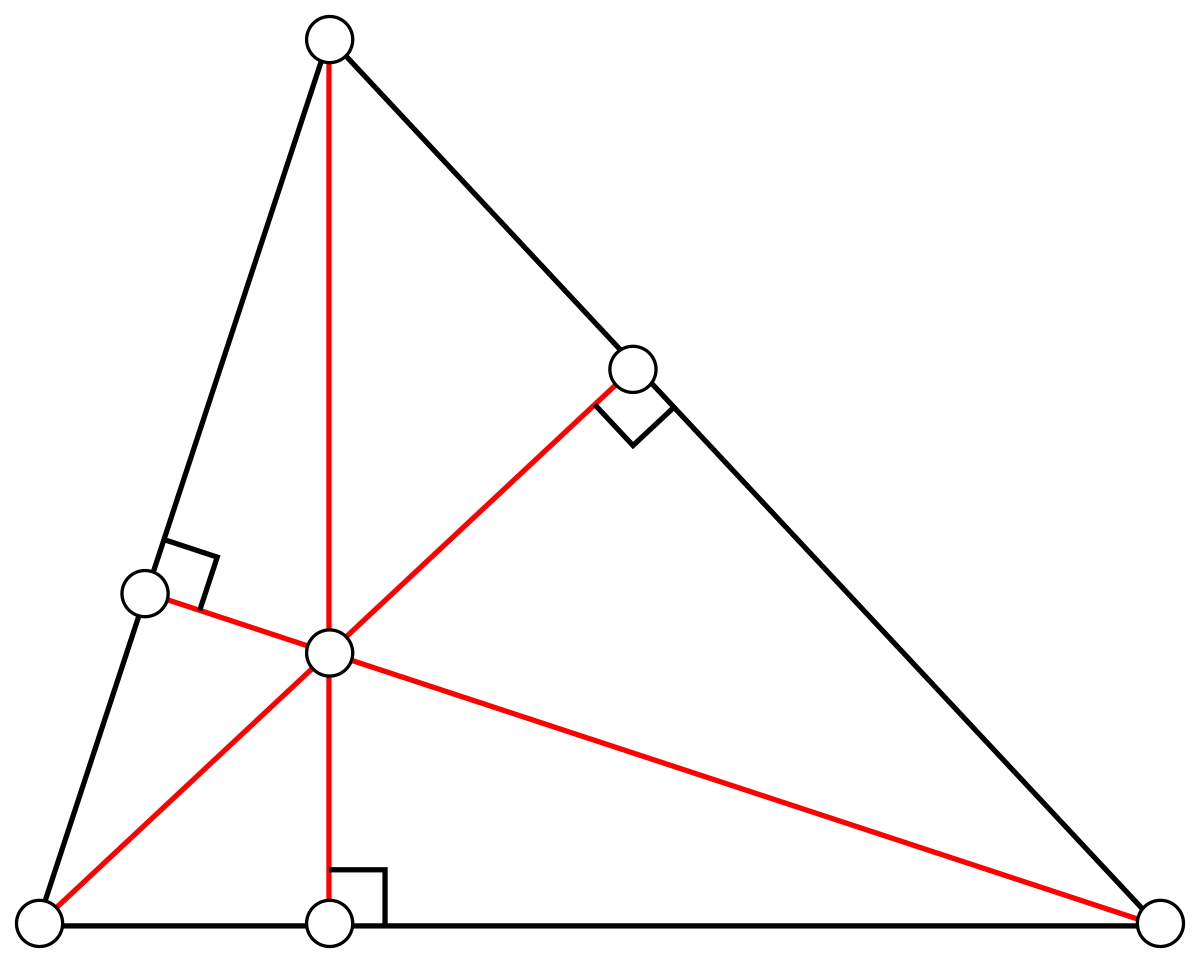
Mediatrices
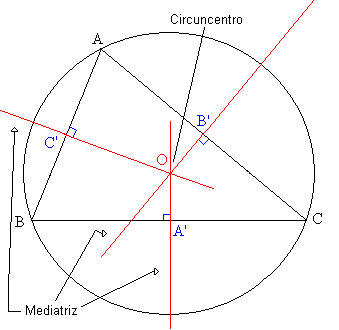
Son tres, una por cada lado del triángulo. La mediatriz es una línea recta que pasa por el punto medio del lado de triángulo al cual corresponde. Las tres mediatrices de un triángulo se intersectan en un punto conocido como circuncentro, el cual se encuentra a la misma distancia de cada uno de los vértices del triángulo.
Bisectrices
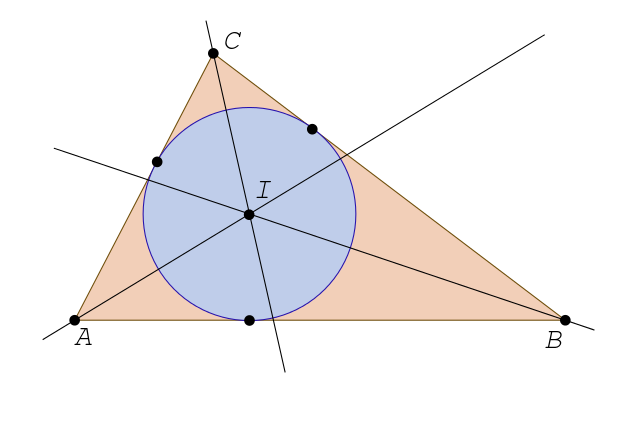
Son tres, una por cada ángulo. La bisectriz es una línea recta que parte del vértice y divide al ángulo en dos partes iguales. Las bisectrices de un triángulo se intersectan en un punto conocido como incentro.
Medianas
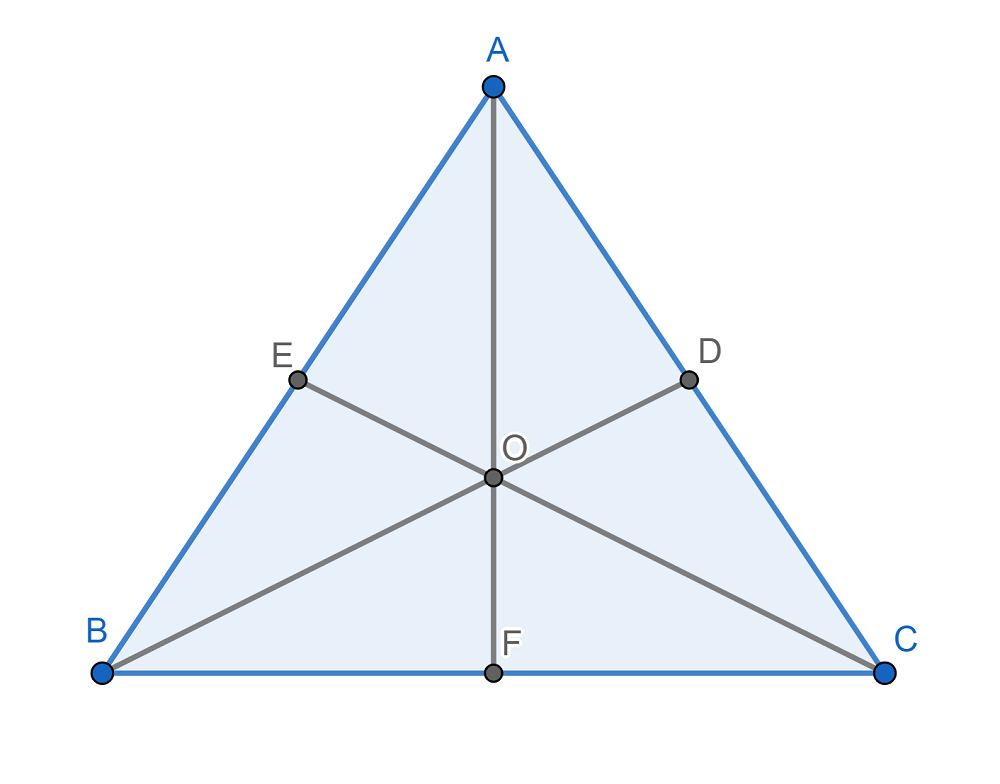
También son tres, una por cada vértice. Una mediana es una recta que parte de un vértice y llega hasta el punto medio del lado opuesto. Las medianas de un triángulo se intersectan en un punto llamado baricentro.
La distancia que hay entre cualquiera de los tres vértices y el baricentro equivale a dos tercios (2/3) de la longitud total de la mediana correspondiente. Por ejemplo, si la mediana CE mide 5 centímetros, entonces la distancia entre C y el baricentro (O) es igual 5 x 2/3, o lo que es igual, a 5 x 0,66, lo que da como resultado 3,3 centímetros.
Alturas
Es una línea recta que une un vértice con el lado opuesto. Las tres alturas de un triángulo se intersectan en un punto llamado ortocentro. Según el tipo de triángulo, el ortocentro puede hallarse dentro o fuera del área del triángulo.
¿Cómo calcular el área del triángulo?
El área de un triángulo de cualquier tipo se puede conocer al aplicar la siguiente fórmula:
A = b x h / 2
En esta ecuación, A se refiere al área; b hace referencia a la base y h es la altura.
Veamos un ejemplo. Se nos pide que calculemos el área de un triángulo cuya base mide 12 centímetros y cuya altura es de 7 centímetros. Así, pues, tenemos:
b = 12
h = 7
Aplicamos la fórmula:
A = 12 x 7 / 2
A = 84 / 2
A = 44
Este triángulo tiene, por tanto, un área de 44 centímetros cuadrados.
